4.4 Примеры решения задач

1 Призматический брус под действием собственного веса.

Брус жестко закреплён верхним концом и находится под действием сил веса направленных вдоль его продольной оси ОХ.

Длина бруса l, площадь поперечного сечения А, удельный вес и модуль Юнга материала соответственно γ и Е. Построить эпюры нормальных напряжений Ϭ(x) и перемещений u(x).

Решение.

Реакция в точке закрепления R=γAl. Продольная сила N(x)= γA(l-x), её график на рис. 4.6б.

Рис. 4.6 Брус под действием

собственного веса

Нормальные напряжения Ϭ(x)=N/A= γ (l-x). На основании (4.19) u(x) = u(0) + γ (l-x) dx= (2lx -x²). Следовательно, наибольшее перемещение получит сечение x = l, т.е. свободный конец стержня. Это перемещение по модулю равно общему удлинению Δl = l². Учитывая, что вес стержня G=γAl, последнюю формулу можно представить в виде

что в два раза меньше, чем от приложения силы N=G, но к концу этого же стержня (4.21).

Контрольные вопросы к лекции 4

1. Какая должна быть у бруса ось и как должны быть приложены силы, чтобы возникала деформация чистого растяжения – сжатия

2. Равнодействующие внешних сил приложены вдоль оси прямого бруса. Какая возникает деформация? Каковы внутренние силы и как их определить?

3. Как определить нормальные напряжения при растяжении – сжатии?

4. Запишите условие прочности при растяжении – сжатии

5. Виды механических испытаний конструкционных материалов

6. Примеры материалов, одинаково сопротивляющихся растяжению и сжатию

7. Какие образцы используются для испытаний на для испытаний на растяжение?

8. Что такое длинный образец?

9. Что такое короткий образец?

10. Изобразите диаграмму растяжения мягкой конструкционной стали. Укажите и разъясните характерные точки этой диаграммы

11. Что такое предел пропорциональности?

12. Что такое предел упругости?

13. Что такое предел текучести?

14. Что такое предел прочности?

15. В чем заключается явление текучести материала?

16. Какие материалы имеют развитую площадку текучести? Имеет ли это технологическое значение?

17. В чем заключается явление наклепа? Какое технологическое значение оно имеет?

18. Назовите характеристики прочности материала?

19. Назовите характеристики пластичности материала?

20. Что такое абсолютная линейная деформация?

21. Какова размерность абсолютной деформации? Почему?

22. Что такое относительная линейная деформация?

23. Что такое угловая деформация?

24. Связь деформаций и перемещений при растяжении – сжатии(формула Коши)

25. Дифференциальные уравнения для определения перемещений при растяжении – сжатии

26. Закон Гука при растяжении

27. Объясните, что такое коэффициент Пуассона

28. Что такое модуль Юнга?

29. Какова размерность модуля Юнга? Почему?

Лекция №5

Статическая неопределимость в курсе сопротивления материалов. Методические рекомендации по изучению темы. Общий подход к решению статически неопределимых задач. Решения в усилиях и в перемещениях. Примеры раскрытия статической неопределимости стержневых систем работающих на растяжение-сжатие.

Цель: На примере простых стержневых систем работающих на растяжение-сжатие, путём параллельного изложения метода сил и метода перемещений ознакомить курсантов с общими приёмами раскрытия статической неопределимости.

Рекомендованная литература: [ 1 стр.72-101, 2 стр. 68-72, 3 стр.147-152, 4 стр.40-44]

Введение. В курсах сопротивления материалов знакомство с решением статически неопределимых задач ограничивается, как правило, использованием уравнений в усилиях и метода сил [1-4] при замалчивании других путей синтеза (метода деформаций и смешанного метода). Последнее, вероятно, оправдано при первом знакомстве с этой простейшей наукой из цикла прочностных. Однако в ряде случаев уже на этапе анализа первых задач представляется возможность без особого труда рассмотреть альтернативные пути раскрытия статической неопределимости.

Цель лекции. С точки зрения автора целесообразно ознакомить студентов, как с методом сил, так и с методом перемещений уже при освоении раздела растяжение – сжатие, а так же использованием статически неопределимых основных систем в методе сил при расчёте статически неопределимых балок и в условиях дефицита аудиторного времени подготовить будущих специалистов к самостоятельному творческому освоению прогрессивных методов конструирования и расчёта (например, программных комплексов МКЭ базирующихся преимущественно на методе перемещений [5]).

Методические рекомендации. Начиная изучать курс сопротивления материалов, необходимо обратить внимание:

- на его общие методологические основы как науки: абстракция, анализ и синтез, феноменологический подход;

- на статическую неопределимость задачи сопротивления материалов вообще и отмечать этот факт при изучении каждой простой деформации;

- на общую методику решения всех статически неопределимых задач.

Анализ статически неопределимой задачи всегда идет по одной и той же схеме: три стороны задачи - статическая, геометрическая (кинематическая), физическая (закон деформирования: линейные или нелинейные зависимости между усилиями и деформациями). Последовательность их рассмотрения, в принципе, может быть произвольной.

Синтез же зависимостей, найденных при анализе можно провести тремя путями. Исключить деформации (перемещения) – получить разрешающие уравнения в напряжениях (усилиях), исключить усилия (напряжения) – получить разрешающие уравнения в перемещениях (деформациях). Отдельно стоит редко применяемый смешанный метод.

Первое знакомство студентов со статически неопределимыми задачами происходит при завершении изучения раздела растяжение – сжатие. Начинают, с какой либо относительно простой задачи, как правило, один раз статически неопределимой. Далее следует обычная цепочка рассуждения: количество неизвестных реакций превышает число уравнений равновесия (статическая сторона задачи, понятие степени статической неопределимости), для составления дополнительных уравнений предлагается рассмотреть упругую систему в деформированном состоянии (кинематическая и физическая стороны). И, наконец, синтез за редкими исключениями в направлении замены деформаций в уравнениях совместности силовыми факторами.

Ниже, на примерах обобщающих некоторые классы задач из методичек и пособий [2], предлагается методика параллельного ознакомления студентов с основными способами раскрытия статической неопределимости: решениями в усилиях и в целом более эффективными [5, стр.68] решениями в перемещениях (выше уже отмечено, что при определённых условиях приходят к методу сил и методу перемещений в канонической форме).

Рассмотрим две простые задачи, для которых применение метода перемещений в ряде случаев предпочтительно и задачу, в которой за счёт использования статически неопределимой основной системы метод сил сравнивается в эффективности с методом перемещений (в каждом примере своя нумерация рисунков и формул).

Пример №1

Рис. 1 Расчетная схема Рис. 2 План перемещений

Абсолютно жесткий диск шарнирно закреплен в точке О и удерживается от поворота n упруго-деформируемыми стержнями. К диску приложена система сил действующая в плоскости XOY имеющая относительно центра приведения О главный вектор R₀ и главный момент M₀. Требуется найти усилия в стержнях N_i (i=1,2,…n) при n>1 (при n=1 задача статически определима) и составляющие реакции в шарнире R_х и R_у.

Выполним анализ задачи. Для удобства изобразим отдельно только i-й удерживающий стержень до и после деформации (рис. 2)

1 Статическая сторона задачи

Уравнения равновесия статики запишутся:

(1)

2 Геометрическая сторона задачи. Из плана перемещений (рис. 2) следует: 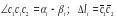следовательно,

(2)

где r_i - модуль радиус – вектора шарнира с_i , соединяющего i-й стержень с диском, γ – неизвестный угол поворота абсолютно жесткого диска, обусловленный деформацией стержней.

3 Физическая сторона задачи

Полагая деформации стержней линейно – упругими, имеем:

(3) где (4)

E_i, A_i и l_i – соответственно модуль Юнга, площадь поперечного сечения и длина i-го стержня.

Линейная система 3-х уравнений (1), n уравнений (2) и n уравнений (3) (всего 3+2n уравнений) содержит неизвестные R_x, R_y, γ, Δl_i, N_i количество которых также 3+2n. Следовательно, решая совместно систему (1), (2), (3), можно с учетом принятых допущений однозначно определить все неизвестные и оценить прочность и жесткость заданной упругой системы.