Корректность по тихонову
Математик делает всё, что можно и так, как нужно.
Физик делает всё, что нужно и так, как можно.
Инженер делает всё, что нужно и так, чтобы оно работало.
Алекс Алдер
1. Постановка задачи
Пусть
обратная зaдача
неустойчива
на паре метрических пространств
,
то есть
оператор
не
является непрерывным
на
.
Рассмотрим
поведение
оператора
в
окрестности
точки
,
где
–
компакт
и
“настолько мал”,
что
операторы
и
непрерывны.
Определение. Операторное уравнение называется корректным по Тихонову, если:
1) априори
известно, что точное решение
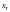задачи
находится внутри заданного (компактного)
множества
множества (класса) корректности, то
есть
;
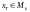2) априори известно, что точное решение задачи единственно на множестве , то есть оператор А обратим на множестве ;
3) можно показать непрерывную зависимость решения от возмущений правой части.
Комментарий.
Мы уже отмечали
ранее, что оператор, обратный к вполне
непрерывному оператору, действующему
в бесконечномерных гильбертовых
пространствах, не является ограниченным.
Если A –
вполне непрерывный оператор, а
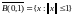
шар
в пространстве
,
то
компакт.
Если оператор
непрерывен, то
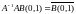должен
быть компактом. Шар является компактом
только в конечномерном пространстве.
Поэтому оператор
не
может быть непрерывным.
Но нельзя ли использовать дополнительную информацию для того, чтобы, по крайней мере, сузить множество возможных решений. Идея А.Н.Тихонова: если известно, что множество решений компакт, то задача решения операторного уравнения корректна при условии, что приближенная правая часть его принадлежит образу компакта.
2. Отличие от классического понятия корректности
1. Для уравнения, корректного по Тихонову, не доказывается теорема существования, а предполагается, что решение существует априори. ( Принцип Ландау: если уравнение верно описывает явление, то его решение существует и единственно, потому что существует и единственна реальность, которую оно описывает).
2. Точное решение единственно на множестве корректности, а не на всём пространстве.
3. Непрерывную зависимость от параметров нужно доказывать на множестве корректности, а не на всём пространстве.
Таким
образом, корректность восстанавливается
за счёт сужения класса возможных решений
до
или сужения класса возможных правых
частей до
.
Поэтому корректность по Тихонову
называют ещё и условной
корректностью
или условной
устойчивостью.
Комментарий. Корректность по Тихонову естественна с физической точки зрения.
В самом деле, классические теоремы существования устанавливают существование решения в определённых функциональных пространствах. Однако даже в приведенных примерах некорректных задач для дифференциальных уравнений не имеют места теоремы существования классического типа.
В частности, в задаче Коши для уравнения Лапласа, чтобы существовало решение, необходимо и достаточно, чтобы некоторая комбинация данных была аналитической функцией, аналитически продолжаемой в ту область пространства, где определяется решение задачи. Очевидно, что выполнение сформулированного условия не гарантируется принадлежностью данных какому-либо функциональному пространству, и в формулировке достаточных условий решения задачи Коши для уравнения Лапласа надо прямо или косвенно учитывать производные всех порядков от этой комбинации данных.
Аналогичные
условия необходимы и для того, чтобы
существовало решение задачи Коши для
уравнения теплопроводности с обратным
временем и для задачи аналитического
продолжения. Эти условия носят не
конструктивный характер, их выполнение
не может быть проверено непосредственно
из показаний приборов (тогда как
принадлежность данных, например,
пространству
может быть проверена даже визуально,
если данные представлены в виде графика).
С другой стороны, существование решений
рассматриваемых задач и принадлежность
их определенным множествам оказываются
естественными с точки зрения соответствующих
физических постановок.
Второе требование единственность решения в понятии корректности по Тихонову не отличается от этого же требования в понятии классической корректности, если ограничиться рассмотрением только множества корректности. Однако, как было отмечено выше, такое ограничение является естественным с точки зрения математического описания реальных физических систем.
Последний этап исследования задачи на условную устойчивость заключается в том, что требуется установить факт непрерывной зависимости решения от начальных данных на множестве корректности и получить оценки нормы изменения решения через норму изменения начальных данных.