14.3 Энергетическая и специфическая избыточная мощность
Полная энергия объединяет потенциальную и кинетическую энергии как:
.
А выражая через удельную энергию это уравнение можно записать в виде:
|
(14.4) |
При постоянной величине энергии возможен переход от кинетической энергии к потенциальной, что особенно значимо для военных самолётов. Пренебрегая любыми различиями в величинах тяги двигателя и самолёта (то есть при поддержании постоянной величины энергии) совершающего полёт с числом Маха М = 0.9 на высоте уровне моря (что соответствует V = 306 м / сек) возможно «изменение масштаба полёта», то есть поднятие на высоту 4 777 м, где полностью отсутствует продольная скорость. Более того, самолёт, совершающий полёт на высоте, скажем, в15 км при числе Маха М = 0.9, что соответствует скорости V = 266 м / сек, может «изменить масштаб полёта» до высоты в 18.6 км.
Способность совершения манёвров ускорения или скороподъёмности зависит от избытка тяги свыше требуемого, необходимого для поддерживания баланса тяги для установившегося полёта. Мера этого баланса характеризуется отношением избытка тяги к весу самолёта, которая может быть записана в виде:
,
где FN – максимальная чистая тяга (тяга нетто) двигателя, а D – сопротивление самолёта. (И тяга двигателя и сопротивление функции, зависящие от высоты и скорости полёта). В более традиционном и понятном виде, удельная мощность (или удельная избыточная мощность ), SEP, выражается через произведение меры баланса на скорость V, в единицах скорости:
|
(14.5) |
.Во время совершения манёвров, при выполнении которых увеличивается величина лобового сопротивления, подобно тем, что обсуждались в разделе 14.3, при той же самой величине тяги двигателя величина SEP падает. Доступная максимальная скорость подъёма при постоянной скорости полёта, эквивалентна величине SEP. Принимая во внимание, что доступная норма ускорения в полёте (то есть увеличение скорости) равна удельной избыточной тяге ( SEP / V ) · g , удельная избыточная мощность связывается с удельной энергией через уравнение:
|
(14.6) |
.SEP = 0 соответствует режиму полёта при постоянной скорости на постоянной высоте с двигателем, производящим максимально возможную тягу. На рисунке 14.5 схематично показан участок, для которого SEP = 0. Граница кривых SEP = 0 установлена аэродинамикой самолёта, его весом и тягой двигателя. На рисунке 14.5 тяга двигателя была бы максимальной для каждой точки высоты при соответствующем ей числе Маха полёта. Поскольку самолет испытывает эффект торможения, при М = 1.0 и SEP = 0 падений кривой в этой области подразумевает более низкий статический потолок . Самолёт может оказаться вынужденным работать внутри границы, заданной условием SEP = 0 по причинам, обозначенным на рисунке.
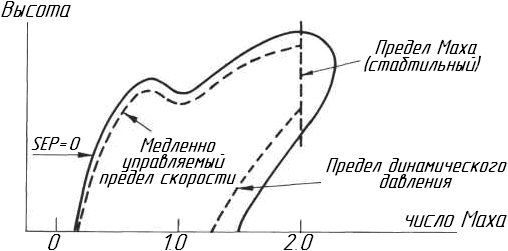
Рисунок 14.5. Схематический график высота- число Маха, показывающий линию SEP = 0 для боевого самолета. Наложена граница управляемого устойчивого полета.
Кривые SEP = Const, показанные на рисунке 14.6 построены для самолёта-истребителя для трёх уровней перегрузки. Рисунки показывают контуры, построенные на осях числа Маха и высоты; для участка с перегрузкой в 1 · g, который соответствует прямому полёту на уровне кривой полной энергии. Кривая SEP = 0 передаёт в каждом случае предел устойчивого действия при максимальной тяге двигателя и, перемещающегося внутри этого контура самолёта с повышающейся величиной SEP. Поскольку величина перегрузки увеличивается, то область, для которой SEP ≥ 0 уменьшается. При совершении переворотов (и других сложных манёвров), когда величина перегрузки больше единицы, граница SEP = 0 определяет предел поддерживающей нормы поворота. Самые высокие величины SEP проявляются во всех условиях при низкой высоте и дозвуковом диапазоне чисел Маха. При этом условии высокая плотность воздуха приводит к понижению величины коэффициента подъёмной силы (поэтому понижается индуктивное сопротивление) и повышению тяги нетто двигателя.
Рисунок 14.6. Схематические показанные участки, характеризующие связь высоты и числа Маха для военного самолёта, учитывая фактор перегрузки.
Для большей конкретизации отметим, что кривые, изображённые на рисунке 14.6 показывают, что для величины перегрузки в 3 · g в манёвре разворота на высоте в 30 000 футов (или 9.1 км) при М = 0.9, величина SEP стремится к нулю. Соответствующий участок для величины перегрузки полёта в l · g при заданной комбинации высоты полёта и числа Маха показывает, что SEP ≈ 150 фут / сек; так с двигателями, дающими максимальную тягу самолёту, статическая энергия увеличилась бы, или ускорилась бы в направлении полёта на величину 150 фут / сек (или 47.5 м / сек). Полетная скорость для числа Маха с М = 0.9 для этой высоты равно 273 м/сек, а ускорение в направлении полета составит ( SEP / V ) · g = (47.5 / 273) · g, или 0.17 · g. Для совершения манёвра поворота при величие перегрузки 5 g, существует отдельный участок, изображённый на рисунке 14.6, где показана комбинация высоты и числа Маха, при которой SEP ≈ - 400 фут / сек (что соответствует - 122 м /сек), и самолёт или теряет высоту полёта при этой скорости или замедляется по курсу (122 / 273) · g = 0.45 · g.
На рисунке 14.7, изображён график зависимости высоты от числа Маха, имеющий отношение к двум самолётам, F-5 и более поздней версии F-20. Более устойчивым является F-20 это очевидно, но менее очевиден тот факт, что самолёт совершает полёты на меньших диапазонах скоростей и высот, а величина перегрузки достигает 4· g, по сравнению с l · g. Первичная зона сражения в диапазоне высот от уровня моря, до тропопаузы и числе Маха полёта меньше единицы. Из-за низкой плотности воздуха на большой высоте совершения полёта, процессы маневрирования становятся затруднительными, до тех пор пока на сверхзвуковых числах Маха радиус выполнения переворотов (или угла крена) не станет на столько большим, что продолжение боя станет невозможным.
Рисунок 14.7. График зависимости высоты полёта от числа Маха для самолётов F-5E и более поздней версии F-20.