11.4 Центральный компрессор ( компрессор вд)

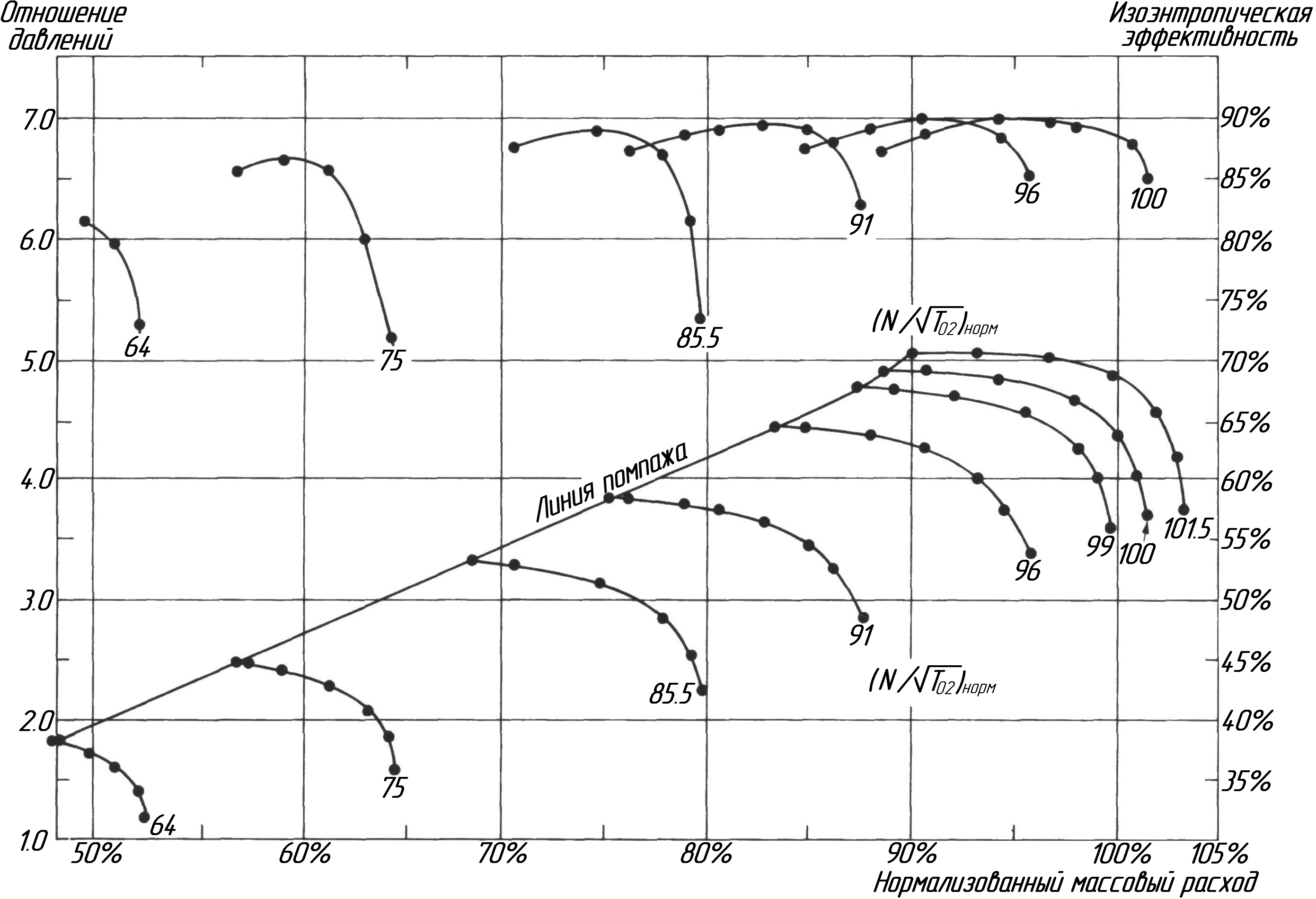
_{Рисунок 11.5. Характеристика современного компрессора.}

На рисунке 11.5 представлена характеристика современного компрессора, выражающая зависимость степени повышения давлений и изоэнтропической эффективности от массового расхода , вдоль линии безразмерной постоянной угловой скорости, исходя из параметров на входе в центральный компрессор:

,

массовый расход выражается как процентное соотношение к расчётным данным. Максимальное отношение давлений для этого компрессора равно 5, значит, он подходит для трёхвального двухконтурного двигателя. Отношение давлений равное 6 представляет собой верхний предел, который может быть достигнут без регулирования статоров, причина этого будет рассмотрена ниже в этом разделе. Регулируемые статоры настраиваются так, что скорость в компрессоре падает, статоры нескольких передних рядов поворачиваются вдоль тангенциального направления потока, таким образом уменьшая угол атаки.

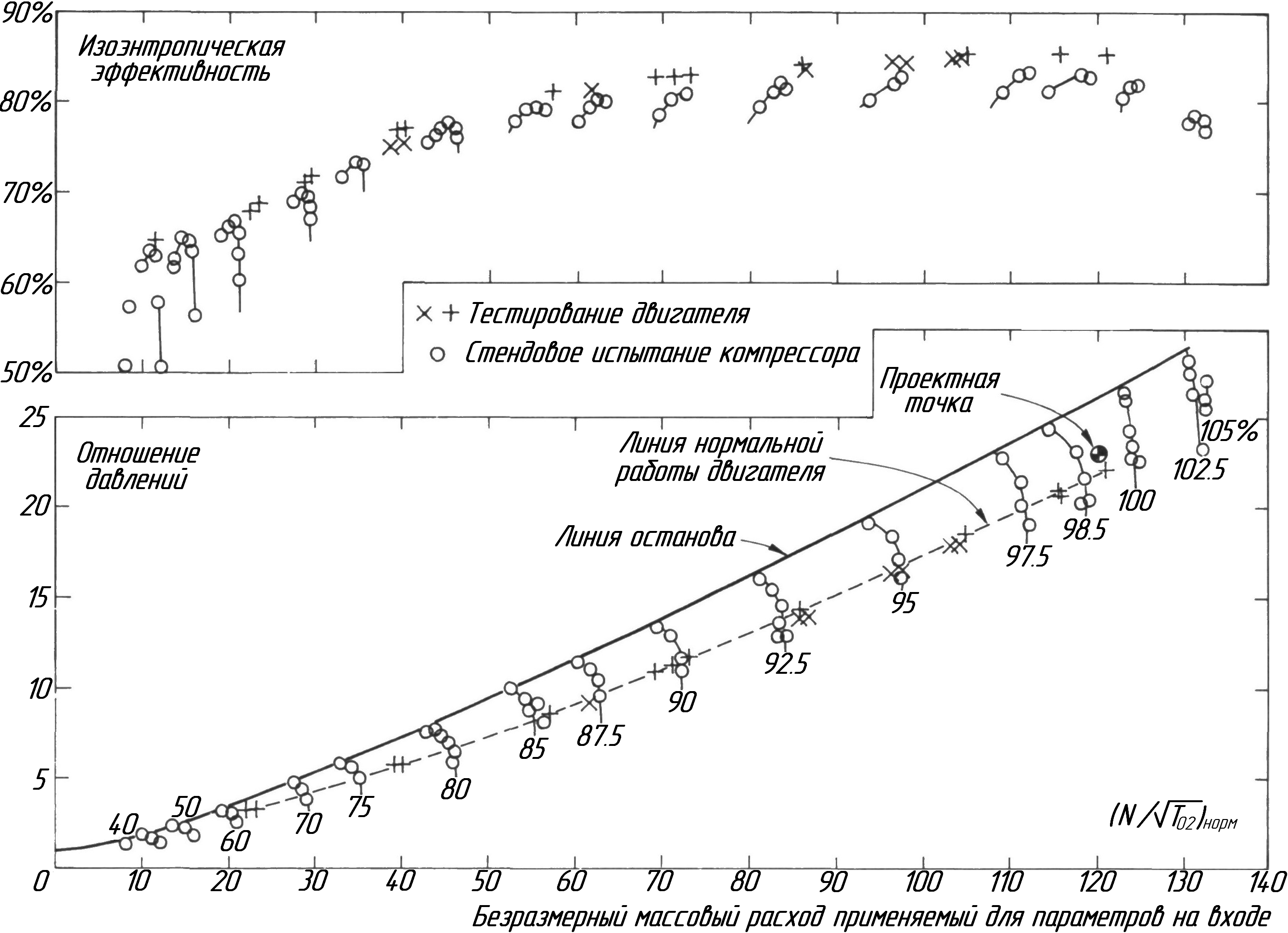
Рисунок 11.6. Характеристики компрессора «GE E³».

На рисунке 11.6 представлена характеристика компрессора «GE E³», отражающая функцию отношения давлений и изоэнтропической эффективности от безразмерного массового расхода для линий постоянной безразмерной угловой скорости. На рисунке 11.6 представлены переменные компрессора со степенью повышения давления равной 25. Это компрессор «GE E³» (Двигатели с эффективным использованием энергии), который в измененной форме является центром (или газогенератором) двигателя «GE90». В этом компрессоре на первых 6 ступенях (включая входной направляющий аппарат вентилятора перед первым ротором) находятся регулируемые статоры. Отметим, что при высоких скоростях кривые скоростей демонстрируют запирание для низких степеней повышения давления. Два типа данных, отображённых на этом рисунке, показывают результаты проверки компрессора на установке с переменным дросселем (показано свободными символами), а также данные, полученные в двигателе (показано перечеркнутыми символами). Данные, полученные на установке, представляют собой кривые скоростей.

11.4.1 Определение эффективности, изоэнтропическая и политропическая эффективность

На рисунках 11.4, 11.5 и 11.6 представлена изоэнтропическая эффективность, определяемые уравнением 11.1, также их иногда называют адиабатической эффективностью. В многоступенчатых компрессорах и турбинах полезно дать ещё одно определение эффективности, которое несколько отличается- это политропическая эффективность - η_P. Использование политропической эффективности облегчает некоторые алгебраические расчеты и он удобен при сравнении машин с различными степенями повышения давления.

Рассмотрим случай небольшого роста заторможенного давления δP_0, сопровождаемого ростом температуры и энтальпии δТ₀ и δh₀. Уравнение состояния примет вид:

,

где δh₀ = C_P · δT₀, а δs₀ = δs. Для процесса идеального адиабатического повышения давления, при котором δs = 0, изменения энтальпии и давления связаны соотношением:

можно объединить состояния 1 и 2 следующим образом:

.

Фактический рост температуры для реального процесса повышения давления будет больше, чем идеальный, и может быть записана через политропическую эффективность:

Которое даст:

	для компрессора	(11.2)
	для турбины	(11.3)

Упражнение 11.2

Покажите, что политропическая эффективность для процесса сжатия между заторможенными состояниями 1 и 2 может быть записан как

а адиабатическая или изоэнтропическая эффективность записывается как

, где

Рисунок 11.7. Зависимость изоэнтропической эффективности от политропическй эффективности.

На рисунке 11.7 продемонстрирована связь политропической эффективности с адиабатической одновременно для компрессора и турбины при различных величинах отношения давлений. Для компрессора общая адиабатическая эффективность ниже, чем политропическая, в то время как для турбин он выше; в турбинах этот эффект называется коэффициентом возврата теплоты. Причина более низкойо адиабатическойо эффективности для компрессора может быть объяснена при помощи графика функции зависимости температуры от энтропии, изображённой на рисунке 11.8, которая отображает процесс сжатие между заторможенными состояниями 01 и 03 то есть от 1 до 16 бар, произведённый двумя путями: одним шагом от 01 к 03 при или двумя маленькими одинаковыми шагами от 01 к 02’ и далее к 03’ при . Как было описано ранее, общая адиабатическая эффективность для повышения давления в одной ступени составляет 90%, если в каждой ступени двухступенчатого повышения давления эффективность будет составлять 90%, то значение результирующей температуры T₀₃ повысится, что приведёт к понижению общей эффективности. Другими словами, при разделении процесса повышения давления между ступенями, адиабатическая эффективность каждой ступени должен быть выше, чем общий. Объясняется тем , что температура растёт на первой ступени, прежде чем войти во вторую и в результате температура, во второй ступени выше, чем на первой, даже если отношение давлений и эффективность одинаковы на обеих ступенях. В пределе, когда прирост увеличения давления вдоль ступени стремится к нулю, адиабатическая эффективность ступени приближается к пределу политропической эффективности. Для осевых компрессоров, рост давления на каждой ступени, как правило, небольшой и потому адиабатическая эффективность ступени и политропическая эффективность ступени в основном равны; более того, если на всех ступенях величина эффективности одинакова, тогда политропическая всей машины также будет равна эффективности каждой ступени. Это продемонстрировано в упражнении 11.3. Использование политропической эффективности, поэтому, не подходит для анализа современных задач, но использование его величины даёт лучший результат при сравнении показателей работы машин, имеющих различные степени повышения давлений.

Рисунок 11.8. График зависимости функции температуры от энтропии, отражающий процесс повышения давления.

Упражнение 11.3

а) Предположим, что компрессор имеет десять ступеней, со степенью сжатия 1.3 в каждой. Найдите полную степень повышения давления. Если политропическая эффективность каждой ступени - 90 %, найдите степень повышения температуры через весь двигатель. Подтвердите, что политропическая эффективность всего двигателя - 90 %, и найдите изоэнтропическую эффективность ступени, η_isen,st и всей машины, η_isen,ov

б) Предположим, что степень сжатия ступени остается 1.3, но для первых пяти ступеней эффективность равна 90 %, а для последних пяти ступеней - 80 %. Найдите полную степень повышения температуры и отсюда политропическую и изоэнтропическую эффективность для всего двигателя.

Упражнение 11.4

Для вентилятора на рис.11.4 строят рабочую линию для запертого сопла такой, что линия проходит через 100%-ую линию скорости на массовом расходе для максимальной эффективности. (Трех степеней сжатия, одной из которых в расчетной точке, будет достаточно, чтобы построить рабочую линию.) Для упрощения берут η_Р = 0.90 для все рабочей линии.

Примечание: рабочая линия для запертого сопла не дает хорошее соответствие между рабочей линией и положением максимальной эффективности.

Упражнение 11.5

Для компрессоров, показанных на рис. 11.5 и 11.6, вычислите политропическую эффективность соответствующую наибольшей изоэнтропической эффективности на расчетной (100%) скорости для каждого компрессора.

Каждый компрессор был проверен с использованием запертой турбины. Предполагая, что сопло заперто и его площадь является постоянной (то есть постоянный удельный массовый расход), нарисуйте рабочую линию на рис. 11.6. Рабочая линия должна проходить через степень сжатия 22.5 на 100 % линии скорости.

Упражнение 11.6

Для компрессора, изображенного на рис.11.6, перерисуйте 100 %, 90%-ые и 80%-ые линии для постоянной скорости в координатах безразмерного массового расхода, основанного на условиях на выходе. Примите постоянной значение политропической эффективности на каждой линии скорости в расчете температуры на выходе - упрощения, которое не будет существенно изменять форму характеристики - и возьмите значение η_P, полученное в упражнении 11.6. для 100% скорости, 0.86 на 90% скорости и 0.83 на 80% скорости.

Примечание: безразмерный удельный массовый расход, основанный на условиях на выходе, может быть равным на разных скоростях. Дело обстоит так, например, на степени сжатия 22.5 на 100% скорости и приблизительно 12 и 7 для 90 % и 80 % соответственно, соответствует рабочая линия, изображенная в упражнении 11.6.