11.2 Реактивное сопло

Потоки внешнего и основного контуров могут иметь отдельные реактивные сопла или смешиваться между собой, образуя общее реактивное сопло. В любом случае поток на входе в реактивное сопло считается однородным; неоднородность вносит небольшой вклад в коэффициент расхода, величина которого меньше единицы. (Коэффициент расхода – это отношение фактического массового потока к массовому потоку, получающемуся при расширении на выходе до статического давления без потерь и однородном потоке с площадью, равной геометрической площади реактивного сопла). Для запертого реактивного сопла с углом сужения составляющим 5º, коэффициент расхода составляет 0.97, тогда как коэффициент скорости равен 0.998, как видно, ошибка в расчётах и погрешность невелики, следовательно, этим можно пренебречь при дальнейшем изложении материала. При высоких скоростях полёта обычно используются сопла Лаваля, однако для летательных аппаратов, совершающих полёты на дозвуковых скоростях стоимость и вес таких сопел не оправдывают затраты на эксплуатирование.

Изменение безразмерного массового расхода, проходящего через сужающееся сопло с отношением давлений (давление торможения потока статическое давление на выходе) в сечении сопла показано на рисунке 11.2 для воздуха (с коэффициентом k = 1.40) и для выхлопных газов, для которых принят коэффициент k = 1.30. До этого принималось условие обратимости потока в критическом сечении, которое для сужающегося сопла располагается на выходе из сопла. Увеличения массового расхода по отношению давлений происходит до достижения определенного значения.

Рисунок 11.2. Изменение безразмерного массового потока через сужающееся реактивное сопло.

Как выяснено в теме 6 запирание в реактивном сопле происходит, когда отношение давление торможения равно или в несколько раз больше, чем окружающее статическое давление, т. е. равно 1.89 для случая, когда k = 1.40. Когда сопло заперто, а число Маха в его горле равно единице, тогда безразмерный массовый поток характеризуется как постоянный, другими словами:

.

Для чистого воздуха, проходящего через реактивное сопло второго контура, при

k = 1.40 получаем:

.

Отличается от нашего A(k,R) на величину корня из Ср=1005

Для потока в турбине или в основном реактивном сопле, при k = 1.30 принимаем наиболее соответствующее приближённое значение:

. Отличается от нашего A(k,R) на величину корня из Ср=1265

Массовый поток и все условия на входе в критическое сечение сопла остаются неизменными, как только поток запирается. На рисунке 11.2 показана зависимость и применительно к соплу Лаваля, где A – площадь критического сечения сопла, а P – соответствующее ему давление в критическом сечении сопла. (Изменение изоэнтропической площади в сопле Лаваля показано на рисунке 6.2 в функции от числа Маха; при использовании кривых , также изображённых на рисунке 6.2, может быть выведена зависимость площади от статического давления). Почти во всех случаях реактивное сопло будет заперто; исключение составит сопло внешнего контура, эксплуатируемое на малых скоростях полёта.

Хотя сопло заперто, и состояния вверх по течению в двигателе не меняются, это не означает того, что изменений вниз по потоку за горлом нет, просто их изменение незначительно, хотя это может привести к изменению тяги. Этот процесс хорошо отображён в Упражнении 11.1.

Упражнение 11.1

11.1. Рассмотреть истечение из реактивного сопла в атмосферу с окружающим статическим давлением p_a. Поток на выходе из реактивного сопла (площадь выхода A) имеет однородное статическое давление и скорость, p₉ и V₉; в общем p₉ - не равен p_a. На некотором удалении вниз по потоку давление в реактивном сопле становится равным p_a и на срезе реактивная скорость - V_j. При этом расход в реактивном сопле остается постоянным и равным . Рассматривая подходящий контрольный объем и применяя уравнение сохранения расхода, покажите, что:

Когда степень повышения давления значительно больше критической и сужающееся-расширяющееся сопло с полным расширением потока, покажите, что полная тяга может быть записана в безразмерной форме:

Замечание: состояние в сопле установлено как критическое; безразмерные скорость и массовый поток постоянны, объясните, почему величина увеличения в тяге с настолько мала при больших величинах степени повышения давления.

Рисунок 11.3, основанный на упражнении 11.1, отображает зависимость безразмерной тяги брутто от отношения давлений для обоих сопел для воздуха с k = 1.40. Каждое, простое сужающееся сопло, или сужающееся – расширяющееся сопло имеют достаточное отношение давлений, необходимое для создания полного обратимого расширения. Обратимое расширение происходит внутри сужающегося сопла, а не на выходе из него к самолёту. Сопло дросселируется для создания степеней повышения давления , но эффект необратимости на выходе потока из сужающегося сопла не очевиден до тех пор, пока отношение давлений не превышает значения, равного 3. Это величина заметно выше, чем для современных гражданских двигателей, но намного ниже, чем для скоростных двигателей.

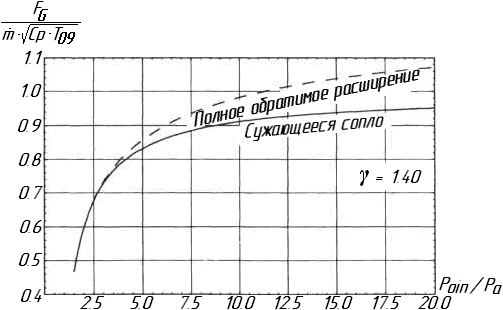
Рисунок 11.3. Представление безразмерной тяги брутто в функции отношения давления торможения на входе к атмосферному давлению на выходе.

В сопле современного двигателя боевого самолёта (истребителя) отношение давлений может достигать 16, потеря тяги в сужающемся сопле при этом составят более 10 %. Из графика, изображённого на рисунке 6.2 можно увидеть, что площадь на выходе из сопла может стать больше площади горла; например, при диапазоне отношений до 16, площадь на выходе из сопла будет в 2.5 раза больше площади критического сечения.