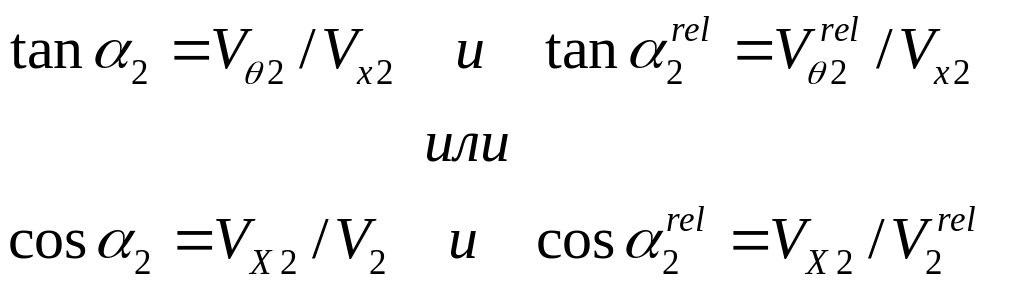9.2(2) Осевая турбина

Концептуально, легче понять работу турбины, чем компрессора, поэтому мы начинаем с рассмотрения турбины. На рисунке 9.4 показаны полторы ступени турбины: ряд статора, далее по потоку ряд ротора и затем второй ряд статора. При проектировании ряды в турбинах располагают близко друг к другу, промежуток при этом составляет около 20 % от хорды лопатки, скорость вращения ротора обычно не отличается от скорости звука. В рядах ротора и статора поток ближе к тангенциальному направлению на выходе, чем на входе. К счастью, ещё давным-давно, был придуман метод, позволяющий с достаточной точностью смоделировать процесс для технических целей, который теперь успешно используется в теории газовых турбин.

Для получения достаточно точных расчётов течения газа в технических целях применяют метод, суть которого состоит в использовании своей системы координат, установленной для ряда лопаток ротора и статора: при рассмотрении ряда статора используют неподвижную систему координат, а скорости при этом характеризуются как абсолютные. Для ротора используется система, которая перемещается с ротором со скоростью U; здесь компоненты скорости характеризуются как относительные.

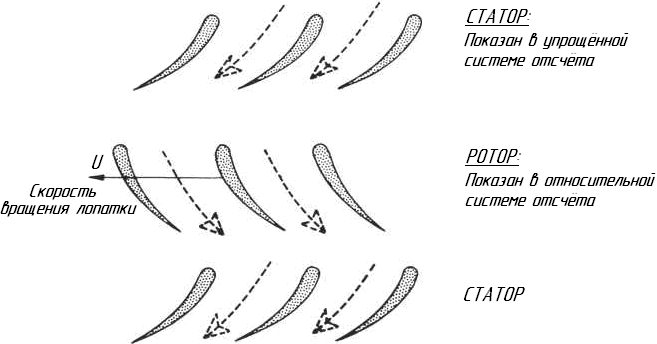
Рисунок 9.4. Схематическое представление ступени осевой турбины.

Состояния на выходе из статора станут состояниями на входе в ротор, и этот переход от относительной к абсолютной скорости будет снова и снова повторяться в каждой ступени. Подход основывается на использовании треугольников скоростей, показанных на рисунке 9.5. Здесь принимаются за абсолютную скорость V, а за относительную – скорость . Поток входит в ряд статора 1 со скоростью V₁, под углом α₁ к осевому направлению. В этом сечении осевые и тангенциальные компоненты представлены в виде: и , соответственно.

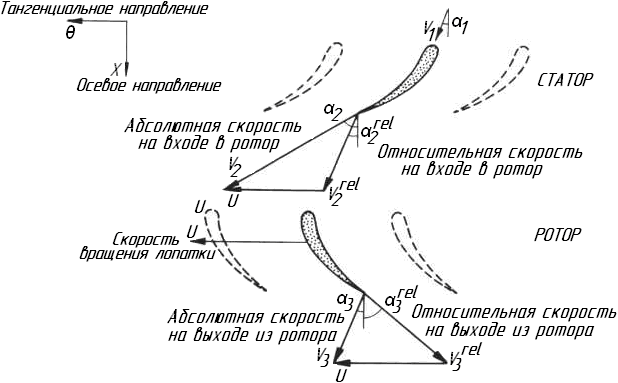
Рисунок 9.5. Осевая ступень турбины и треугольники скоростей.

На выходе из статора абсолютная скорость - V₂, с её осевыми и тангенциальными компонентами, определяемыми так же, как и скорость V₁. Относительная скорость, для наблюдателя, на входе в ротор , может быть получена из векторных дополнений треугольника. Здесь рассматривается тот случай, когда осевая скорость равна, и в абсолютных и относительных системах отсчета, те есть , но тангенциальные скорости отличаются:

.

(9.6)

Из компонентов выражения скорости легко получить различные углы, например:

(9.7)

И так далее для других возможных комбинаций.

Таким же образом задаются условия для выхода потока из ротора:

.

(9.8)

Для упрощения уравнений в обоих случаях принято, что величина скорости вращения лопаток U на входе и на выходе равна, другими словами не учитывается радиальное изменение положения лопаток, через которые проходит поток. Принимая во внимание это ограничение на постоянный радиус легко заметить, что энтальпия торможения на входе и на выходе из ротора, при использовании аналогичной (или той же самой) системы координат, остаётся величиной постоянной, то есть:

,

где

.

(9.9)

Аналогичная ситуация наблюдается для лопаток ряда статора, для которых проявляется признак торможения энтальпии в абсолютных координатах. (Хотя для ряда статора это утверждение остаётся истинным даже при различных радиусах). В роторе и статоре, даже при отсутствии потерь, относительное давление торможения будет постоянным; фактически, потери происходят и в ряде лопаток турбины между 3 % и 6 % выхода, при этом обычно теряется динамическое давление лопаток.

Уравнение работы Эйлера показывает абсолютное понижение энтальпии торможения при переходе через ступень, показанной на рисунке 9.5:

,

(9.10)

с введением ограничения по постоянному радиусу выражение упрощается. Это уравнение может быть переписано в терминах относительной тангенциальной скорости как:

,

(9.11)

где и направлены в одну сторону, так как скорость вращения лопаток ускоряется.

Если осевая скорость выбрана величиной постоянной, в соответствии с уравнением (9.10), тогда выражение упрощается и принимает вид:

,

(9.12)

которое эквивалентно:

,

(9.13)

где и направлены в одну сторону в соответствии с выбранными направлениями скоростей и .

Этот обмен работы происходит даже при реальных потерях. Эффект потерь должен создать большее снижение давления, чем для случая с той же самой температурой, при изоэнтропической потере. Если проект машины неудовлетворителен, однако, количество потерь может возрасти, обычно ограничиваются диапазонам подобных потерь и .

Ступень турбины может быть представлена как расширяющийся ряд лопаточного венца, в котором скорость увеличивается. Если высокое давление, существующее в камере сгорания расширить в отдельной ступени, тогда действительно разовьётся высокая скорость (приблизительно 1 450 м / сек), которую не будет возможно использовать эффективно по назначению. Хитрость турбины заключается в том, что каждый ряд должен создавать меньшее расширение, обычно согласующееся со скоростями звука на данной ступени, а затем, изменяя систему отсчёта, уменьшить её на выходе к следующему лопаточному венцу. Этот процесс можно наблюдать на рисунке 9.5, где скорость, на выходе из статора, в абсолютной системе отсчёта, довольно высока, но соответствующая ей скорость на входе в ротор уже заметно меньше по величине. Аналогично скорость, на выходе из ротора высока в относительной системе отсчёта, но соответствующая ей скорость в абсолютной системе отсчёта на входе в статор заметно ниже. Каждый ряд лопаток турбины принимает поток, направление которого не очень отличается от осевого направления, и поворачивает его в сторону тангенциального, таким образом, сокращая площадь потока и увеличивая его скорость.

Упражнение 9.6

В упражнении 9.5 была установлена безразмерная работа на выходе из ступеней основной турбины на среднем радиусе. Возьмите Vx/Um = 0.55 и предположите, что во всех ступенях поток является осевым в каждом ряде статора в абсолютной системе отсчета; это определяет треугольник скоростей на выходе из ротора так же, как условия на входе в статор. Найдите направление потока из лопаток статора. Предположите, что осевая скорость является постоянной от входа до выхода. Изобразите треугольники скоростей и эскиз поперечного сечения лопатки, чтобы получить желательную нагрузку. (Предположите, что направление потока то же самое, что и на выходе из лопатки). (Ответ: α₂ = 74.6 °)

Упражнение 9.7*

Длина лопаток турбины в радиальном направлении еще не была выбрана. Предположите, что поток заперт на выходе из первой ступени статора. Зная массовый расход, температуру торможения (которая равна 1450К на крейсерском режиме и не падает в статоре) и давление (принятое равным давлению на выходе из компрессора), можно найти требуемую площадь. Рассчитайте проходное сечение, приняв высоту лопатки h короткой относительно среднего радиуса так r_m. Средний радиус был найден в упражнении 9.5. Используйте его, чтобы найти h на входе в первый ротор.

(Ответ: h = 38 мм)

Изобразите схему основной турбины в осевом-радиальном направлении. Предположите, что площадь увеличивается в обратной пропорциональности с плотностью, основываясь на использовании вычисления в условиях торможения Т₀/ρ₀^k-1=constant. Для основной турбины коэффициент пропорциональности основан на осевом проецировании хорды (относительное удлинение - пролет лопатки, разделенный на ее хорду) не должно быть меньше одного и не должно превышать 2.5.

Упражнение 9.8*

Угловая скорость ротора низкого давления установлена в соответствии с требованием окружной скорости лопатки вентилятора: принято, что угловая скорость вращения ротора низкого давления - 53 об/с (3180 об/мин). Если скорость лопатки турбины низкого давления может быть высокой, что означает возможность большего среднего радиуса, мы можем иметь меньше ступеней для того же самого коэффициента нагрузки. Но слишком большой средний радиус не является удовлетворительным. Для турбины низкого давления мы должны выбрать количество ступеней (приемлемым считается до шести ступеней), однако, в весовом и стоимостном отношении число ступеней более 4 является затруднительным.

Используйте направляющие линии, ∆h₀/U_m² не должен превысить 2.5 и Vx/Um не должно превысить 1.0 для турбины низкого давления, чтобы найти средний радиус турбины низкого давления и требуемое число ступеней. (из упражнения 7.1 снижение температуры в турбине низкого давления - приблизительно 361 К для bpr = 6 и около 376.2 для bpr = 10.) Предполагают, что поток только осевой в абсолютной системе координат в каждом венце статора, так как это делает эти оценки намного легче; это предположение - обычно недалеко от действительности.

(Ответ: для bpr = 6; с 5 ступенями r_m/<0.51 м., с 4 ступенями r_m/< 0.572 m).

Сделайте некоторые эскизы возможных расположений, допуская относительное удлинение, основанное на осевых проекциях хорды, в пределах 4.