6.3 Запертое сопло

Представляет интерес другая проблема, специфическая для сжимаемого потока, она касается, максимума потока, который может проходить через сечение с заданной площадью. На рисунке 6.1 показан поток истекающий из] бассейна или большого объема через реактивное сопло, для которого минимальная площадь приходится на горло. Предполагая здесь, что поток одномерен (другими словами, поток однороден в перпендикуляре к направлению течения и что он является adiabatic, массовая величина потока через единицу площади горла дается

(6.8)

и в установившемся потоке максимальная величина м очевидно находится в горле. Поскольку течение aдиабатическое уравнение энергии потока, уравнение 6.1, ведет к виду

или 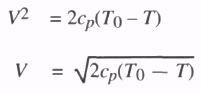(6.9)

Где Т - местная температура воздуха, и То обозначает температуру торможения, которая постоянна повсюду для потока. Для изоэнтропического потока

или (6. 10)

Где массовая величина потока может быть записана

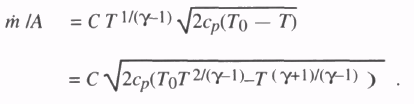(6.11)

Замена этого в уравнение 6.9

Который упрощает к

(6.12)

скорость звука.

Другими словами, массовая величина потока через отверстие или реактивное сопло - достигает максимума, когда скорость в горле звуковая.

Для большинства эксплуатационных режимов реактивного двигателя реактивное сопло будет заперто. (Это имеет место, в газовой турбине, там турбина также эффективно заперта.)

6.4 Приведенный массовый поток

В уравнении (6.11) расход выражен в терминах местного Числа Маха потока М. и после некоторых алгебраических манипуляций, массовая величина потока через единицу площади дается в безразмерной форме выражением

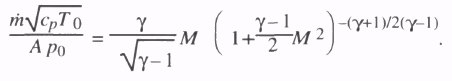(6.13)

Эта функция так широко используется, что удобно обозначить это символом m так, чтобы

(6.14)

Для данного газа m - функция только Числа Маха, и это показано для воздуха (y = 1.40) на рис. 6.2. Обратите внимание, что в горле, когда М = 1,

(6.15);

Таким образом в горле .]

для y=1.4, m. = 1.281,

для у = 1.30, m. = 1.389.

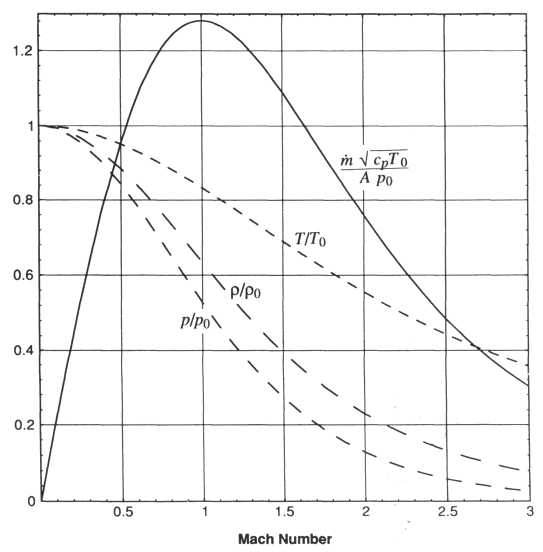
Рисунок 6.2. Одномерный поток совершенного газа, k = 1.4

Уравнение 6.15 показывает очень ясно, что массовый поток через запертое реактивное сопло - пропорционален давлению торможения потока и обратно пропорционален квадратному корню заторможенной температуры. Единственный способ изменять массовый поток через запертое реактивное сопло данного размера изменять или давление торможения или температуру торможения. Изменение условий после реактивного сопла не оказывает никакого эффекта на массовый поток или на состояние вверх по течению от горла.

Три других кривых показаны на рис. 6.2. Одна кривая - отношение статической температуры к температуре торможения

Другие две кривые дают соответственно отношение местного статического к давлению торможения и плотности для изоэнтропического течения по реактивному соплу.

и

РЕЗЮМЕ ТЕМЫ 6

Уравнение Бернулли не имеет силу для потока газов, если Число Маха более приблизительно 0.3; что обычно имеет место в реактивных двигателях. Давление торможения поэтому может быть определено, используя

Массовый поток через единицу площади может быть дан в безразмерной форме, которая для заданных свойств газа, - однозначная функция Числа Маха и отношения удельных теплоемкостей

И эта безразмерная форма будет использоваться в связи с анализом работы

Величина потока через запертое реактивное сопло определена давлением и температурой торможения вверх по течению и независима от условий вниз по потоку от горла. Для реактивных двигателей реактивное сопло обычно заперто; это относится также к большинству турбин.

Упражнение 6.1

Расписать выражение P₀ / P в уравнении:

,

используя разложение по формуле бинома, чтобы выразить отношение в форме:

.

Определите значение самого высокого числа Маха, при котором может использоваться выражение для давления торможения с условием несжимаемости, если величина погрешности не должна превышать 1%? Какова величина погрешность в вычислениях давления торможения для уравнения Бернулли при числе Маха М = 0.3.

(Ответ: 0.20, 2.25 %)

Упражнение 6.2*

Определите величины температуры торможения и давления потока, воспринимаемые самолётом, совершающим полёт на крейсерском режиме с числом Маха полёта M = 0.85 на высоте 31 000 футов.

(Эти величины были приняты в упражнении 5.1).

(Ответ: 259.5 K, 46.0 кПа)

Упражнение 6.3

Самолет летит с числом Маха 2 на высоте 51000 футов (p_a = 11.0 кПa, T_a=216.7 К) движимый простым турбореактивным двигателем (без второго контура). При нахождении температуры торможения и давление на входе кв компрессор считать воздухозаборник изоэнтропическим, компрессор имеет отношение давлений 10 с изоэнтропическим кпд 90%: найдите температуру и давление на выходе из компрессора. (Ответ: 793.3 K; 0.861 MПa)

В камере сгорания скорости низкие (так что давление торможение и статическое давление равны), но абсолютное давление торможения падает на 5%. При входе в турбину температура торможения - 1400 К; кпд турбины 90%. Найдите температуру торможения и давление за турбиной.

(Ответ: 996.7 K; 0.212 MПa)

Если реактивное сопло изоэнтропическое, найдите скорость реактивного сопла, полагая полное расширение в реактивном сопле. Вычислите полную тягу, удельную тягу, тяговый кпд и температурный перепад камеры сгорания, полный кпд.

(Ответ: V_j = 1069 м/с; F_G = 1069 Н/кг/с, F_N = 479 Н/кг/с, η_р = 0.711, η_о = 0.464)

Упражнение 6.4

Двигатель с большой степенью двухконтурности, сопло второго контура может запираться, когда самолет летит при числе Маха 0.85. Пренебрегая любыми потерями в давлении торможения вверх по течению и вниз по потоку вентилятора, вычислите степень повышения давления вентилятора, при котором реактивное сопло второго контура не будет запираться. (Ответ: 1.18)

Упражнение 6.5

Для простого турбореактивного двигателя из упражнения 6.3 (нет внешнего контура) найти площадь горла реактивного сопла на единицу массового расхода, далее по потоку стоит расширяющееся сопло - найти выходную площадь сопла, если расширение - изоэнтропическое до статического давления окружающей атмосферы. (Ответ: 0.00369 м²кг^-1с; 0.010 м²кг^-1с)

Упражнение 6.6

Для простого турбореактивного двигателя, принятого в упражнении 6.3 (у которого отсутствует второй контур), определите величину площади горла реактивного сопла (или его критического сечения), приходящегося на единицу массового расхода, если учесть, что далее по потоку расположено расширяющееся сопло. Определите заключительную величину площади, если процесс расширения является изоэнтропическим до выхода в окружающую атмосферу, где давление становится статическим.

(Ответ: 0.00369 м² · кг^-1· с; 0.010 м² · кг^-1· с)

Тема 7

Выбор степени двухконтурности 7.0 Введение

В этой теме мы начнём выбирать степень двухконтурности и вместе с ней отношение давлений вентилятора. Полное отношение давлений и отношение температур T₀₄ / T₀₂ были выбраны в теме 5. После того, как мы выберем степень двухконтурности и отношение давлений, мы определим расход воздуха, необходимый для получения требуемой тяги на крейсерском режиме; определение тяги было рассмотрено в теме 2.