Тема 6 Элементы механики течения сжимаемого газа

6.0 Введение

В рассмотрении газовой турбины существенно сделать надлежащее подтверждение сжимаемого характера(природы) продуктов сгорания и воздуха. Механика сжимаемого газа - сложный предмет, но здесь дается только то, что является существенным для понимания изложения и выполнения проектов. Существуют специальные подходы для анализа течения сжимаемого высокоскоростного потока во внутренних каналах, рассмотрение их - цель этого раздела.

6.1 Несжимаемый и сжимаемый поток(течение)

Для жидкостей изменение плотности обычно незначительно, и возможно обращаться с потоком как несжимаемым. Таким образом, уравнение для установившегося без трения течения упрощенно

и может быть интегрировано непосредственно, принимая плотность постоянной, это дается уравнением Бернулли

где Pо - заторможенное или полное давление , соответствует давлению, полученному когда поток приведен в состояние покоя без трения или без потерь, член 0,5V2 известен как давление динамическое или динамическая добавка. Трубка pitot делает запись давления торможения принимая во внимание, что давление у стенки, параллельной потоку, делает запись статического давления. Использование давления торможения кое-что вроде бухгалтерского упражнения - оно указывает давление, которое является достижимым в движущемся потоке. Это иллюстрировано на рис. 6.1. Аналогия, которая является иногда полезной, может быть взята из гидравлической и механической систем: статическое давление аналогично потенциальной энергии, а динамическое давление аналогично кинетической энергии.

Когда имеют дело с газами с низкой скоростью (более точно, с низким числом Маха) плотность изменяется немного, и возможно использовать уравнение Бернулли как разумное приближение. Погрешность параметров становится существенной, когда динамическое давление становится существенной долей абсолютного давления газа; это происходит, когда Число Маха превышает приблизительно 0.3. Для большинства реальных процессов внутри реактивного двигателя число Маха - ближе к 1.0, чем к 0.3 и из уравнения Бернулли следуют показанные на рисунке 6.1 варианты.

Рисунок 6.1. Схематичное представление состояния торможения

6.2 Статическое и заторможенное состояния

Уравнение энергии установившегося потока газа без передачи теплоты и без передачи внешней работы может быть записано

Где h - enthalpy, которое может быть переписана в более удобном для нас виде как

" (6.1)

То - температура торможения, являющаяся той температурой, которую газ достиг бы, если перешел в состояние покоя без работы и передачи теплоты, не обязательно в идеальной форме или без потерь.

Удельная теплоемкость может быть выражена по уравнению Майера при подстановке в вышеприведенное уравнение температура торможения может быть записана

(6.2)

Скорость звука выражается в виде ,а Число Маха , тогда

уравнение для температуры торможения приобретает вид

(6.3)

Снова, это уравнение между температурой торможения То и статической температурой T не подразумевает идеальное или без потерь ускорение или замедление. Чтобы найти соответствующее отношение между давлением торможения и статическим давлением требуется некоторая идеализация.

В этом случае мы предполагаем, что ускорение или замедление газа между статическим и заторможенным является обратимым и adiabatic (то есть изоэнтропическим), для которого мы знаем

(6.4) Из этого сразу следует

или (6.5)

При работе со сжимаемым потоком принято использовать абсолютные давления и температуры (имеется в виду не избыточное давление и не градусы Цельсия).

Нужно заметить, что до этого раздела не подчеркивалось различие между статическими и температурами торможения, для описания тех явлений не было необходимости их различать. С этого момента мы должны быть более осторожны. В вычислениях таких величин как скорость звука или плотность воздуха, в котором перемещается самолет, это - статические величины. В выполнении исследований цикла, например, выделение работы при высокой температуре в газовой турбине должна использоваться величина торможения. Возвращаясь к бухгалтерской аналогии, использование свойства торможения, как температуры торможения так и давления, дает меру общей суммы энергии, которая является доступной для ускорения потока. Состояние торможения - не реально, кроме как в местах, где скорость может походить на ноль, например, на носу самолета, но статические свойства реальны. Плотность воздуха, скорость звука и параметры химических реакций зависят от местных статических свойств.

Для неподвижной атмосферы (то есть без ветра, V = 0) статические и свойства торможения равны, но наблюдатель в самолете, передвигаясь через неподвижную атмосферу не видел бы, что статические и свойства торможения равны. Наблюдатель, передвигаясь со скоростью V, или Числом Маха М. чувствовал бы температуру торможения, равную

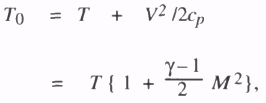(6.6)

И давление торможения, определяемое через изоэнтропическое отношение, как

(6.7)

Фактор скорости должен увеличить полное отношение давлений в двигателе. В своем входном отверстии двигатель получает температуру и давление торможения. Для полета с Числом Маха 0.85 давление торможения входного отверстия связано с окружающим давлением уравнением (6.5) и выше в 1.604 раза Поток на выходе реактивного сопла, однако, реагирует на окружающее статическое давление pa так, что в результате полета отношение давления в двигателе будет увеличено в 1.604раза.