2.3 Уравнение дальности Брегэ
Улучшенный показатель аэродинамического сопротивления крыла, который способен сохраняться в полёте для данной тяги двигателя, приводит к увеличению массы летательного аппарата. В дальнейшем будет выяснено, что этот показатель не является первичным оптимальным значением для пассажирского самолета; вместо этого каждый хочет осуществлять перелёты на максимально возможные дистанции. Перелёт на максимально возможную дальность, которая будет достигаться при оптимальном выборе режимов аэродинамики и полёта, будет характеризоваться отношением ML/D. Наиболее часто пассажирские самолёты совершают полёт на крейсерском режиме на высотах, в которых изменение температуры не очень заметно, так оптимальное число Маха, аэродинамический показатель и отношение ML/D, фактически эквивалентны, для самолёта Boeing 747-400 они показаны на рисунке 2.3. Подобно рисунку 2.2, на котором для каждого режима полёта максимальное число Маха соответствует коэффициенту подъёмной силы 0.5, но отличительной чертой этого графика является наличие максимума ML/D, при котором существует наибольшее значение числа Маха составляющее M = 0.86. Но чем больше величина числа Маха, тем резче падает кривая зависимости, отражающая коэффициент ML/D. Именно из-за быстрого падения этого коэффициента при высоких числах Маха, его значение для режима крейсерского полёта принимается M = 0.85.
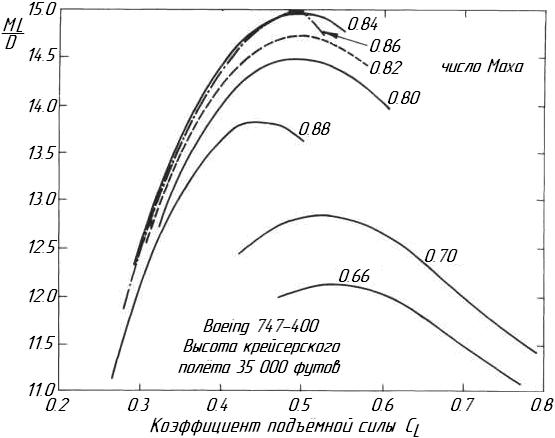
Рисунок 2.3. Зависимость коэффициента подъемной силы для различных чисел Маха
Разумным было бы поддержание полёта с показателем близким по значению к коэффициенту ML/D, что позволит сохранить значение коэффициента подъёмной силы постоянным с учетом уменьшения объёма топлива и снижения веса летательного аппарата. Такое состояние достигается увеличением высоты полёта, и соответственно уменьшением плотности воздуха. Если высота полёта не будет увеличена, то снижение веса самолёта приведёт к уменьшению коэффициентов CL и ML/D, что вызовет отклонение от оптимального положения.
В оценке дальности полёта мы рассматриваем только крейсерский режим, пренебрегая расстоянием во время осуществления взлёта и посадки – хотя это и не правильно, и разумнее было бы проводить расчёт на дальность отталкиваясь от 12-ти часового полёта. Принимая во внимание, что при полёте на длинные дистанции приблизительно 4% объёма топлива будет расходоваться при выполнении взлёта и подъёма на высоту крейсерского полёта; эта пропорция будет иметь больший показатель для более короткой дистанции. Доля для совершения посадки имеет меньший показатель, но топливо необходимо для осуществления посадки в другом аэропорту, отличным от пункта назначения, если в этом появится необходимость.
Чтобы оценить дальность полёта, мы должны знать отношение расхода топлива к тяге, обычно эта величина характеризуется удельным расходом топлива и обозначается sfc (или tsfc). За единицу расхода топлива принимаем кг / сек топлива на ньютон тяги, которая обозначается кг ∙ сек-1 ∙ Н-1, или
(м / сек)-1.
Во время крейсерского полёта масса самолета w изменяется по формуле:
Где L/D – коэффициент подъёмной силы, при этом w ≡ L. Преобразуем выражение:
Это уравнение может тогда быть переформулировано для нахождения расстояния:
Самолёт приобретает максимальную дальность полёта, если величина коэффициента VL/D близка к максимальной, этот коэффициент может сохраняться как величина постоянная в течение всего круиза за счёт увеличения высоты полёта. При сохранении коэффициента VL/D и удельного расхода топлива постоянными, вышеупомянутое уравнение может быть представлено уравнением дальности полёта Брегэ:
|
(2.2) |
Где wstart и wend - полный вес самолёта в начале и конце круиза соответственно. Как было отмечено ранее, летательный аппарат вероятнее всего должен совершать полёт с постоянным коэффициентом ML/D, а не VL/D, хотя различие между этими коэффициентами мало. Поддержание коэффициентов VL/D или ML/D требовало бы медленного, но непрерывного набора высоты, обычно составляющего для летательного аппарата 4 000 футов. Однако из уравнения дальности полёта Брегэ, мы видим, что диапазон полёта зависит от характеристик самолета; структуры веса, формирующего большую часть полёта и аэродинамического сопротивления крыла при полёте со скоростью, пропорциональной коэффициенту VL/D. Также мы видим, что дальность полёта обратно пропорциональна удельному расходу топлива.
На самом деле ситуация более сложна чем это кажется, потому что удельный расход топлива - функция от скорости полёта, и в действительности должен достигать своего максимального значения показатель (V / sfc) ∙ (L / D).
Упражнение 2.4
Подтвердите, что удельный расход топлива 1.00 фунт/ч/фунт эквивалентен 0.0283*10-3 кг/(с*Н). Оцените дальность, полученную НБС, если в крейсерском полете L/D = 20, удельный расход топлива = 0.57 фунт/ч/фунт, начальная масса в начале крейсерского полета - 613 тонн, и масса в конце крейсерского полета - 399.5 тонн. Для упрощения предположите, что в течение полета скорость равна МКР = 0.85 на высоте 31000 футов.
(Ответ: 13.9*103 км)
(Примечание: Это равно дальности 7600 морских миль, что слегка меньше, чем заданная дальность, но с некоторой добавкой расстояния на подъем и спуск дальность сравнима.)