Порядок виконання роботи:

1. Скласти алгоритм перевірки належності точки координатної площини, заданої своїми координатами (х, у), другому квадранту.

Результатом виконання такого алгоритму потрібно вважати деякий булів вираз. Причому значення Іст, інтерпретується як відповідь "так, точка (х, у) належить другому квадранту", а значення Хиб — як відповідь "ні, точка (х, у) не належить квадранту, що розглядається".

2. Скласти алгоритм пошуку найбільшого значення з трьох чисел у = max(a, b, c).

Для пошуку найбільшого значення з трьох чисел скористаємося виразом max(a, b, c) = max(max(a, b), c).

Отже для знаходження y необхідно послідовно обчислити дві величини

y1 = max(a, b);

y2 = max(y1, c),

для чого досить однієї змінної y.

3. Скласти алгоритм щоб обчислити .

4. Маємо на вході n чисел. З'ясувати, чи всі вони позитивні.

Визначимо числа, що вводяться як а₁, а₂, ..., а_n. Очевидно, нас цікавить умова Q=(а₁ >0) & (а₂ >0) &...& (а_n >0).

5. Скласти алгоритм визначення послідовності чисел, що мають назву чисел Фібоначчи.

Вона задана співвідношенням другого порядку

F₀ = 0, F₁ = 1,

F_k = F_k–1 + F_k–2, k = 2,3,...

Якщо змінна f буде пробігати послідовність Фібоначчи, то двох додаткових змінних sf і t буде досить для позначення подальших двох чисел.

6. Перевірити, що більше n! чи аⁿ. Використовуючи алгоритм з пункту 3.

Контрольні завдання:

1. Побудувати структуровану блок-схему алгоритму, що знаходить суму двох найбільших з трьох  змінних a, b, c.

2. Побудувати структуровану блок-схему алгоритму обчислення факторіала натурального числа.

3. Побудувати структуровану блок-схему алгоритму, який перевіряє правдивість вислову: «Існує трикутник зi  сторонами a, b, c», де a, b, c цілі числа.

4. Побудувати структуровану блок-схему алгоритму, що за номером місяця друкує наступну пору року: "зима", "весна", "літо", "осінь".

5. Побудувати структуровану блок-схему алгоритму, що обчислює біквадратне рівняння ах⁴+вх²+с=0.

6. Побудувати блок-схему алгоритму для визначення типу трикутника (рівносторонній, рівнобедрений, різносторонній) за довжинами його сторін. Якщо трикутник не можна побудувати, слід вивести повідомлення.

7. Записати алгоритм обміну значеннями між двома однотипними змінними.

8. Записати алгоритм циклічного обміну значеннями між трьома змінними a,b,c (a←b, b←c, c←a).

9. Записати алгоритм обчислення таких значень: а⁷,а⁸,а⁶⁴, використовуючи лише операції множення. Де а числова змінна. Операцій множення має бути якомога менше.

10. Задано координати двох точок. Записати алгоритм який визначає, чи належать вони колу з центром в початку координат.

11. Побудувати структуровану блок-схему алгоритму для визначення суми цифр натурального числа N.

12. Побудувати структуровану блок-схему алгоритму визначення суми додатних та кількості від’ємних елементів масиву.

13. Побудувати структуровану блок-схему алгоритму обчислення добутку тих елементів масиву, які належать інтервалу [15; 50].

14. Побудувати структуровану блок-схему алгоритму визначення порядкового номера найбільшого елемента заданого масиву.

15. Побудувати структуровану блок-схему алгоритму визначення для заданої матриці індексу кожного негативного елемента.

Запитання до самоконтролю:

1. Сформулюйте теорему про структурування.

2. Викладіть сутність методів структурування програм.

3. Які методи використовуються для перетворення неструктурованих програм у структуровані.

4. В чому полягає правило простоти?

5. Сформулюйте правило пакетування.

6. Сформулюйте правило вкладання.

7. Які найбільш поширені форми представлення алгоритмів?

Лабораторна робота №2

Технологія низхідного проектування

Мета роботи: вивчення основних прийомів технології низхідного проектування, роботи з функціями; набуття навичок розв’язання задач, що потребують застосування підпрограм.

Теоретичні основи:

Один з ефективних способів створення великих програм, технологія низхідного проектування, полягає в їх конструюванні за принципом „розділяй і пануй”: програма розглядається як набір маленьких фрагментів, кожний з яких виконує певну логічно завершену дію. Такий невеликий фрагмент програмного коду називається підпрограмою. Підпрограма позначається ідентифікатором, тобто має власне унікальне ім’я. Вказування в тексті програми імені підпрограми рівнозначне запису всіх її операторів і називається викликом підпрограми.

В мові PASCAL існує два різновиди підпрограм: процедури та функції. Функція відрізняється від процедури тим, що повертає деяке значення в точку її виклику.

В мові С в якості підпрограм виступають функції.

Функцію в С можна розглядати:

як один з похідних типів даних (поряд з масивами і покажчиками);

як мінімальний модуль програми, що виконується, (підпрограму).

Функція — це елементарна частина програми, відособлена об'єднанням команд, що мають визначену структуру і конкретні ознаки. Функція має окремий власний заголовок і робить яку-небудь дію, задану нею.

Якщо якусь дію потрібно в програмі виконувати декілька раз, потрібно написати відповідну функцію тільки один раз, а потім викликати стільки раз скільки буде потрібно.

Використання функцій підвищує рівень модульності програми і тому полегшує її читабельність, внесення змін і корекцію помилок

Припустимо, треба написати програму для реалізації такої послідовності дій:

– ввести множину чисел;

– впорядкувати їх;

– знайти їх середнє арифметичне;

– надрукувати гістограму

Тоді структура відповідної програми буде мати вигляд:

main()

{

read (list);

sort(list);

average(list);

bargraph(list);

}

Зрозуміло — що треба запрограмувати чотири функції readlist(), sort(), average(), bargraph(), але порядок вирішення задачі вже визначено, тобто видно що програма повинна робити і як вона організована. Додаткова перевага цього підходу полягає в тому, що якщо створити функції достатньо загального типу, тоді їх можна буде використовувати і в інших програмах.

Приклад№ 1

Програма, що використовує функцію для обчислення факторіала та показує таблицю факторіалів для чисел від 1 до 10 на екран:

(мова PASCAL)

program Pr8_1;

uses WinCRT;

var

i: byte;

{ функція }

function factor(x:byte):real;

var

i: byte;

f: real;

begin

f:=1;

for i:=2 to x do f:= f*i;

factor:=f;

end;

{кінець функції }

{ програма }

begin

writeln ('FACTORIAL ');

for i:=1 to 10 do

writeln('I= ',i,' F= ',factor(i):10:0);

readln

end.

(мова С)

#include <iostream.h>

#include <conio.h>

unsigned int factor(int x); // Сигнатура функції

main (){

cout<<"\nFACTORIAL" ;

for (int i=1; i<=10;i++)

cout<<"\ni=" << i <<"\tf=" <<factor(i);

getch ();

return 0;}

unsigned int factor(int x){ // функція

unsigned int f=1;

for (int i=2;i<=x;i++)

f*=i;

return(f);

}

Результат виконання програми:

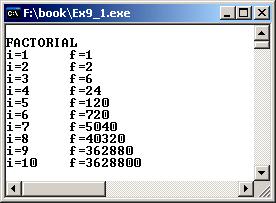
Приклад№ 2

Програма, що використовує функцію для знаходження більшого з трьох чисел та обчислює вираз max(5a,b+a,c+10):

#include <iostream.h>

#include <conio.h>

double fmax(double a,double b){ // функція

if (a>b) return (a);

return (b);

}

main (){

double a,b,c,d;

cout<<"\nEnter a=" ;cin>>a;

cout<<"\nEnter b=" ;cin>>b;

cout<<"\nEnter c=" ;cin>>c;

d=fmax(5*a,b+a);

d=fmax(d,c+10);

cout<<"\nmax=" << d ;

getch ();

return 0;}

Результат виконання програми: