1.3. Содержание отчета

В отчете необходимо привести расчет поправок для однолучевого и многолучевого эхолотов для указанных выше условий. Дать краткие пояснения к выполненным расчетам

1.4. Контрольные вопросы

1. От каких характеристик морской воды зависит скорость распространения звука?

2. Чему соответствует паспортное (эквивалентное) значение скорости звука?

3. Чему соответствует действительное значение скорости звука?

4. Закон Снеллиуса.

ПРАКТИЧЕСКАЯ РАБОТА №2

Обработки данных в океанотехнических измерительных системах

Цель работы

Изучить и освоить методы обработки данных в океанографических измерительных системах

2.1. Теоретический раздел

Обработка данных измерений океанографических величин, полученных с помощью различных измерительных средств, производится на персональных компьютерах. Алгоритмы обработки информации различных измерительных средств имеют свою специфику, обусловленную конструкцией прибора и определяемыми параметрами, а также общими для всех приборов особенностями. К ним относится пересчет кодов N на выходах измерительных каналов в физические величины с помощью содержащихся в формулярах приборов градуировочных коэффициентов C₀ C₁. Обычно для этого используют линейные соотношения вида , но в некоторых случаях( как, например в канале гидростатического давления) – нелинейные уравнения второго и более высокого порядка типа .

В зондирующих приборах применяется операция осреднения данных измерений по заданным слоям и интерполяция результатов на заданную сетку глубин, например. через 1, 5 или 10 м. Это позволяет исключить из данных компоненты, обусловленные качкой судна и упрощает дальнейшую обработку результатов при построении карт, разрезов, вычислениях вторичных физических параметров, таких, например, как соленость, плотность, скорость звука, потенциальная температура и др. Для автономных и буксируемых приборов данные измерений обычно осредняют по заданному числу измерений. Такая операция позволяет эффективно отфильтровывать высокочастотные шумовые составляющие сигналов и выделять необходимые для решаемой задачи участки спектрально диапазона («окна») изучаемого физического процесса.

Важным моментом автоматизированной обработки данных является распознавание и исправление сбоев измерительной информации. Сбои возникают вследствие электрических помех, попадания в рабочие объемы датчиков инородных включений, дефектов записи на магнитные носители и других подобных причин. Для выявления и исправления сбоев используют методы медианой и статистической фильтрации.

Медианая фильтрация производится по заданному нечетному числу отсчетов n следующим образом. Пусть, например, n=5. Алгоритм предусматривает прием пяти чисел x_i, i=1,2,3,4,5 их расстановку по правилу x₁ <x₂ <x₃ <x₄ <x₅. На выход фильтра поступает «среднее» число x₃, которое датируется серединой интервала. Затем производится сдвиг анализируемой последовательности отсчетов на одно последующее значение и операция повторяется. Смысл медианой фильтрации состоит в том, что если в анализируемом блоке имеется сбойное число, то оно обычно или самое большое или самое маленькое, то есть всегда окажется на краю и будет отфильтровано. Алгоритм медианой фильтрации относительно просто реализуется на ПЭВМ. Вместе с тем. этот метод обладает некоторыми недостатками, а именно (1) возможно отклонение результата на выходе фильтра от действительного значения вследствие изменения порядка расстановки отсчетов. Если на участке анализа имеется несколько сбоев, то на выходе фильтра может оказаться один из них. Поэтому иногда, при большом количестве сбоев, медианную фильтрацию применяют несколько раз последовательно.

Статистическая фильтрация производится следующим образом. Анализируемую совокупность отсчетов используют для вычисления стандартного отклонения по соотношению

(2.1)

Затем проверяют каждое число x_i на выполнения условия

, (2.2)

где m =2 или 3 в зависимости от требуемой достоверности анализа. Если соотношение (2.2) выполняется, то с заданной вероятностью оно относится к анализируемой совокупности, если не выполняется, то возможно число x_i является сбоем, его исключают и заменяют интерполированной величиной. Например, при n=2 выполнение условия (2.2) означает. что x_i с вероятностью 95% относится к анализируемой совокупности. Обычно, статистическую фильтрацию необходимо проводить несколько раз последовательно, так как при первых расчетах стандартного отклонения используются сбойные отсчеты. При стабилизации величины стандартного отклонения операцию статистической фильтрации прекращают.

Другой общей проблемой обработки данных измерительных систем является согласование динамических характеристик измерительных каналов при их совместной обработке. В качестве характерного примера рассмотрим СТД зонд, в котором производят последовательные измерения температуры, электрической проводимости и гидростатического давления. В качестве датчика температуры, как правило, используют малоинерционные медные или платиновые термометры сопротивления с показателями тепловой инерции (постоянными времени) T_D, равными примерно 50 мс. Датчик электрической проводимости представляет собой либо четырехэлектродную ячейку, либо трансформатор, в котором морская вода используется как виток связи двух катушек на тороидальных ферритовых сердечниках. Показатель инерции у таких датчиков практически отсутствует. В качестве датчиков гидростатического давления используют либо тензометрические полупроводниковые элементы типа «кремний на сапфире», либо вибрационно-частотные элементы, у которых также отсутствует инерция. Показания всех этих измерительных каналов, т.е. температуры, электрической проводимости и гидростатического давления используют для совместной обработки при вычислениях солености, плотности. скорости звука и других параметров морской воды. При этом, если не принимать специальных мер для согласования динамических характеристик каналов могут возникнуть значительные погрешности при пересечении зондом слоев воды со значительными вертикальными градиентами. В простейшем случае величина такой динамической погрешности равна , где V – скорость опускания зонда, G_T – вертикальный градиент температуры. Обычно скорость опускания океанографических зондирующих систем составляет около 1 м/с, вертикальные градиенты температуры в море могут достигать 1…2 ^оС/м (например, в летний период в верхнем слое Черного моря). Таким образом, динамическая погрешность может достигать 5 10^-2 1 (1…2)=0,05…0,1 ^оС, в то время как инструментальная погрешность канала температуры в современных приборах составляет примерно 0,001...0,002 ^оС, т.е. в 50 раз меньше. Эта погрешность самым существенным образом сказывается на погрешности определения вторичных параметров (солености , плотности и других). Для исключения этой погрешности был разработан специальный алгоритм, описание которого приведено ниже.

Для расчета откорректированных значений температуры t_k предполагается, что на отрезке времени, где производятся три измерения, температура с достаточной точностью описывается кривой второго порядка

, (2.3)

где - пока неизвестные коэффициенты.

Соотношение между температурой среды t_k и показаниями датчика t описываются дифференциальным уравнением первого порядка.

…………………………………….(2.4)

Подставляя в это уравнение (2.3), получаем зависимость изменения температуры воды t_k в следующем виде:

(2.5)

коэффициенты a₀, a₁, a₂ находят для i интервала времени по известным первичным показаниям t_i, t_i+1, t_i+2 при подстановке соответствующих моментов времени в соотношение (2.3):

, (2.6)

где Т – интервал времени между соседними измерениями.

Выражение для текущего откорректированного значения температуры t_ki можно записать в следующем виде:

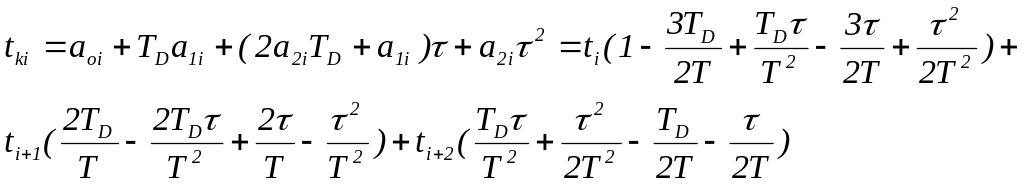(2.7)

Параметры цифрового корректирующего фильтра зависят от порядка расстановки измерительных каналов в течение цикла измерения и от того, к какому моменту времени необходимо производить привязку показаний. Например, в CTD-зондах ИСТОК-3 и ИСТОК-4 была принята следующая расстановка измерительных каналов: 1.Резервный канал, 2.Канал электрической проводимости, 3.Канал температуры, 4. Канал гидростатического давления. Так как измерения электрической проводимости производятся практически без инерции, наиболее рациональной является привязка показаний других каналов к моменту времени измерения электрической проводимости. В этом случае алгоритм корректирующего фильтра имеет следующий вид:

, (2.8)

что соответствует (i+1) циклу измерения электрической проводимости. Следующее скорректированное значение температуры получается скользящим сдвигом показаний на один цикл измерений.

Привязка показаний гидростатического давления к моменту измерения электрической проводимости осуществляется путем линейной интерполяции. Так как соседние моменты измерения давления p симметричны относительно момента измерения электрической проводимости, откорректированные показания канала давления можно представить в следующем виде:

. (2.9)

Таким образом, после i-го измерения электрической проводимости χ_i мы получаем соответствующие откорректированные величины температуры t_k и гидростатического давления p_k. Эти величины используются для вычисления солености, плотности. скорости звука и других параметров морской воды.

Рассмотренный метод цифровой коррекции показаний инерционных измерительных каналов может применяться, в частности, во многих химических измерителях, в состав которых входят, как правило, инерционные датчики типа датчиков кислорода, pH, сероводорода и др.

Глубину погружения океанографических приборов вычисляют по следующему соотношению:

, (2.9)

где z – глубина в м, р – гидростатическое давление в КПа.

До 1976 г при вычислении солености о удельной электрической проводимости, температуре и давлению был принят алгоритм, предложенный Забурдаевым и др. в 1969 г (Морск. гидрофиз. исслед. № 1(43), с.250-254). С целью обеспечения единства измерений при выполнении крупнейшего международного проекта "Полимоде" (1976-1982) был принят алгоритм, предложенный Фофоновым и др.(Woods Hole Oceanogr. Inst. Technic Rep. 1974.-64p). Вычисления солености по этому алгоритму производят методом итераций по следующим формулам:

;

(2.10)

Размерности , , .

В настоящее время используется алгоритм вычисления солености в соответствии со шкалой практической солености ШПС-1978.

Условная плотность и удельный объем морской воды вычисляются на основе уравнения Кнудсена-Экмана по следующим формулам:

Размерности , (2.11)

При обработке данных измерения течений алгоритмы вычислений зависят от конструкции прибора. В самом простом случае измеряется модуль вектора скорости течения V и угол φ между направлением на северный магнитный полюс и направлением вектора скорости течения. Проекции вектора скорости течения на меридиан v и на параллель u равны:

, , (2.12)

где - угол магнитного склонения.

Для осреднения данных о скорости течения используют величины v и u, а не V и φ, так как в этом случае средние величины вектора скорости течения точно соответствуют пути жидкой частицы за время осреднения. Если для осреднения использовать непосредственно измеряемые величины V и φ, результат может значительно отличаться от величины среднего переноса частицы за время осреднения. Например. если в силу каких либо причин вектор скорости флуктуирует относительно нулевого угла и попеременно принимает значения 0⁰ и 360⁰, то среднее значение направления осредненного вектора скорости будет равно 180⁰, т.е. противоположным его действительному значению.

В современных двухкомпонентных измерителях скорости течения (это акустические, электромагнитные, допплеровские инструменты) обработка данных производится следующим образом. Одна из измерительных осей прибора (например oy является продольной , другая, нормальная к ней ось ox – поперечной. В таких приборах предусматривается также измерений угла φ между направлением на северный магнитный полюс и продольной осью oy.

Проекции вектора скорости течения на меридиан v и на параллель u для приборов такого типа равны:

, , (2.12)

При осреднении данных используют значения v и u.