3.2. Расчетная модель погрешностей исон
3.2.1. Модель погрешностей вог
Модель дрейфов ВОГ может быть аппроксимирована в виде суммы нескольких составляющих:
погрешности калибровки начального смещения “нуля” и его нестабильности в пуске, т.е. погрешности практически постоянной на достаточно длительном интервале времени, которую вследствие отсутствия данных о спектре ее изменчивости целесообразно описывать винеровским процессом при соответствующих начальных условиях;
погрешности масштабного коэффициента, которая определяет составляющую, пропорциональную измеряемой величине;
погрешности знания румбовых дрейфов ВОГ, которые обусловлены влиянием внешнего магнитного поля и могут быть представлены в виде первой гармоники от угла поворота ИБ;
составляющей, обусловленной неортогональностями осей измерительного блока ВОГ;
“шумовой” составляющей, характеризующей флуктуационные погрешности гироскопов
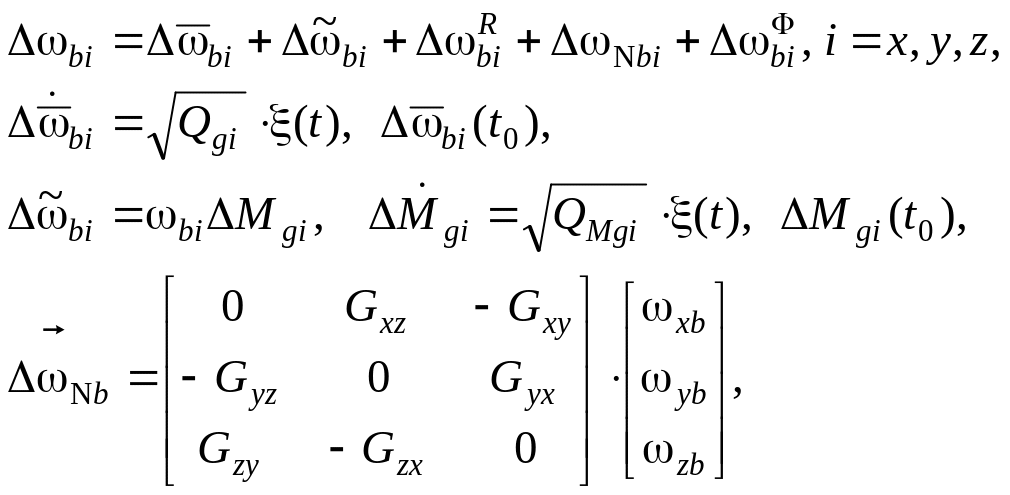(8)
где
– квазисистематическая составляющая
с начальным уровнем
,
характеризуемым погрешностью калибровки
смещения “нуля” ВОГ от пуска к пуску,
и интенсивностью
,
обусловленной нестабильностью смещения
“нуля” в пуске из-за температурных
деформаций гироскопа;
–
погрешность масштабного коэффициента
гироскопа, а
измеряемая им угловая скорость;
составляющие, обусловленные
неортогональностями
(аппроксимированными соответствующими
винеровскими процессами)
осей измерительного блока ВОГ;
”белошумная” составляющая c интенсивностью
;
“белый” шум единичной интенсивности;
румбовые дрейфы ВОГ, обусловленные
в основном влиянием на гироскопы внешнего
аномального магнитного поля.
3.2.2. Модель погрешностей линейных акселерометров
Модель погрешностей линейных акселерометров, как правило, имеет следующие составляющие:
погрешность калибровки начального смещения “нуля” и его нестабильность в пуске, практически постоянную на достаточно длительном интервале, которая может описываться либо случайной постоянной величиной либо интегралом от белого шума;
погрешность масштабного коэффициента, которая определяет составляющую, пропорциональную измеряемой величине;
составляющую, обусловленную неортогональностями осей измерительного блока акселерометров;
шумовую составляющую, характеризующую флуктуационные погрешности датчиков.
С учетом этого инструментальные погрешности линейных акселерометров могут быть описаны следующим образом:
(9)
где
погрешность калибровки начального
смещения “нуля” и его нестабильность
в пуске;
интенсивность изменения квазисистематической
составляющей;
погрешность масштабного коэффициента
акселерометра;
составляющие, обусловленные
неортогональностями
осей измерительного блока акселерометров;
- белошумная составляющая
погрешности, характеризуемая
среднеквадратическим отклонением
на частоте обработки данных;
измеряемое акселерометрами кажущееся
ускорение в осях измерительного
блока
;
“белый” шум единичной интенсивности.
При формировании расчетной модели погрешностей ИСОН использовались следующие аппроксимации:
смещения нулей гироскопов
и акселерометров
,
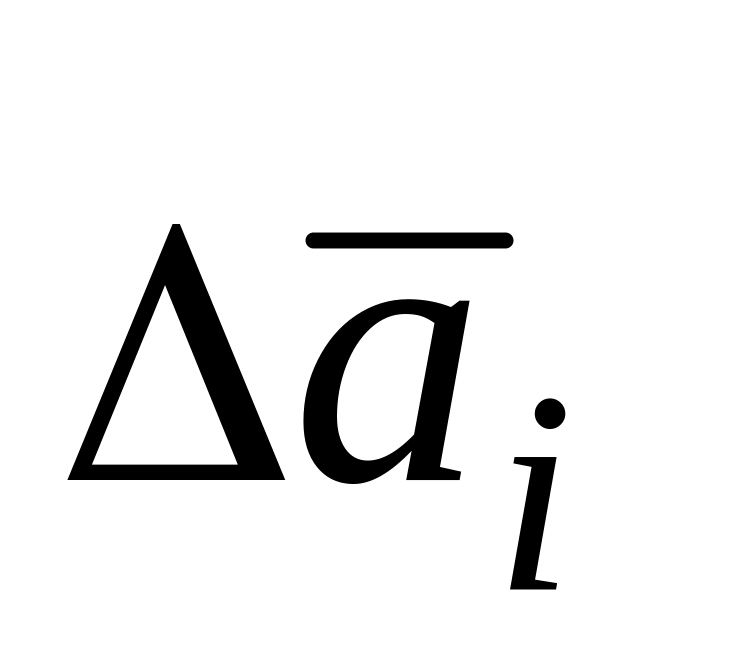изменения систематических составляющих
погрешностей масштабных
коэффициентов
ВОГ от запуска к запуску и
их изменчивость в пуске - были
аппроксимированы (из-за отсутствия
достоверных данных об их спектральном
составе) соответствующими
винеровскими процессами;погрешности знания румбовых дрейфов ВОГ были представлены в виде первой гармоники от угла поворота ИБ
,
(10)
где для условий стенда
(для корабельных условий:
);
искомые коэффициенты
разложения, аппроксимированные
соответствующими
винеровскими процессами
(i
= x,
y);
здесь
курс,
угол поворота ИБ
относительно корпуса БИИМ.
3.2.3. Линеаризованная относительно алгоритма идеальной работы модель погрешностей БИИМ в выработке параметров ориентации и навигационных параметров
Линеаризованная относительно алгоритма идеальной работы модель погрешностей БИИМ в выработке параметров ориентации и навигационных параметров, включающая модели погрешностей в решении задач ориентации, преобразования сигналов акселерометров на навигационные оси и их интегрирования (вычисления составляющих векторов линейной скорости в проекциях на навигационные оси и географических координат места), может быть представлена в следующем виде [1, 2]:
(11)
где
погрешности БИИМ в
аналитическом моделировании горизонтной
системы координат с географической
ориентацией осей (географического
сопровождающего трехгранника)
;
погрешности в выработке
составляющих вектора линейной скорости;
погрешности в выработке
географических широты, долготы и
высоты места;
проекции нескомпенсированных
дрейфов ДУС и так называемых "вычислительных"
дрейфов на оси горизонтной системы
координат;
проекции инструментальных погрешностей
акселерометров на оси горизонтной
системы координат;
погрешность компенсации вертикальной
составляющей вектора нормальной силы
тяжести, обусловленная погрешностями
знания координат места;
,
составляющие уклонения отвесной линии
(УОЛ) и аномалия силы тяжести;
ускорение силы
тяжести нормальной Земли;
средний радиус
Земли;
угловая скорость
суточного вращения Земли;
погрешности компенсации ”вредных”
ускорений по соответствующим осям,
выражения для которых имеют
вид:
(12)
составляющие угловой
скорости вращения горизонтного
трехгранника с географической ориентацией
осей, которые
определяются как
,
,
,
(13)
проекции кажущегося
ускорения на оси горизонтной
системы координат, которые
определяются выражениями:
(14)
3.2.4. Расчетная модель погрешностей системы
В этом случае расчетная модель погрешностей ИСОН будет иметь вид
(15)
где x вектор состояния системы
здесь
погрешности в
выработке соответственно восточной,
северной и вертикальной составляющих
вектора линейной скорости;
погрешности
выработки географических координат
места;
переходная на шаге
матрица системы (15) для момента времени
,
,
(17)
где
единичная матрица
размерности
;
- матрица динамики системы, ненулевые
элементы которой определяются
соотношениями:
,
;
;
;
;
;
;
;
;
,
(18)
здесь
и
текущие значения составляющих вектора
угловой скорости вращения трехгранника
и вектора кажущегося ускорения в месте
установки ИБ
БИИМ, вычисляемые по данным ИСОН [1];
значения
соответственно угловой скорости вращения
Земли, широты места и восточной
составляющей линейной скорости объекта
относительно Земли;
элементы матрицы
направляющих косинусов, определяющих
взаимную ориентацию связанного с ИБ
трехгранника
(b) и горизонтного
географического трехгранника ENH
(h);
матрица, определяющая
влияние вектора входных шумов
с ковариациями
,
где
- диагональная матрица интенсивностей
входных шумов
,
соответствующая модели погрешностей
системы (15) с учетом моделей погрешностей
гироскопов (8, 10) и акселерометров (9).