
Критерий оптимальности.
Если
известны потенциалы решения Х0 транспортной
задачи и для всех незаполненных ячеек
выполняются условия
![]() ,
то Х0 является оптимальным планом
транспортной задачи.
,
то Х0 является оптимальным планом
транспортной задачи.
Если план не оптимален, то необходимо перейти к следующему плану (таблице) так, чтобы транспортные расходы не увеличивались.
Для
перераспределения плана перевозок с
помощью цикла перерасчёта сначала
находят незаполненную ячейку (r, s), в
которой
![]() ,
и строят соответствующий цикл; затем в
минусовых клетках находят число
,
и строят соответствующий цикл; затем в
минусовых клетках находят число
![]() Далее
составляют новую таблицу по следующему
правилу:
Далее
составляют новую таблицу по следующему
правилу:
В плюсовых клетках добавляем Х;
Из минусовых клеток вычитаем Х;
Все остальные клетки вне цикла остаются без изменения.
Цикл перерасчёта таблицы - это последовательность ячеек, удовлетворяющая условиям:
одна ячейка пустая, все остальные занятые;
любые две соседние ячейки находятся в одной строке или в одном столбце;
никакие три соседние ячейки не могут быть в одной строке или в одном столбце.
Пустой ячейке присваивают знак + , остальным - поочерёдно знаки - и + .
После пересчета цикла получаем новую таблицу, дающую новое решение Х, такое, что F(X1)<=F(X0). Вычисляем потенциалы новой таблицы и проверяем оптимальность полученного плана перевозок с помощью критерия оптимальности. Если план не является оптимальным, определяем цикл пересчета и переходим к следующей таблице и т.д. до тех пор, пока критерий оптимальности не будет выполнен.
Вырожденность в транспортной задаче
Вырожденность в транспортной задаче возникает, когда одна или более базисных переменных обращаются в 0.
При построении первого базисного решения могут возникать трудности, если суммы по строкам и столбцам равны между собой и обратились в 0. В этом случае из дальнейшего рассмотрения следует исключить только одну из них. Другая сумма будет ликвидирована при присвоении базисной переменной значения 0. Поскольку на каждом шаге удаляется только одна строка или только один столбец, то в результате количество базисных переменных не меняется (даже если некоторые базисные переменные обратились в нуль).
Трудности могут возникать и при улучшении базисного допустимого плана. Применение правил может обратить в нуль более одной базисной переменной. В этом случае важно помнить, что только одна из них должна стать не базисной, остальные следует сохранить базисными, но с нулевыми значениями.
Пример 1
Фирма должна отправить некоторое количество изделий с трёх складов в пять магазинов. На складах имеется соответственно 15, 25 и 20 изделий, а для пяти магазинов требуется соответственно 20, 12, 5, 8 и 15 изделий. Стоимость перевозки одного прибора со склада в магазин приведены в таблице.

Как следует спланировать перевозку, чтобы её стоимость была минимальной?
Решение. Построим опорный план для рассмотренной выше задачи. В начале построим его с помощью метода "минимального элемента".
Исходная транспортная таблица:
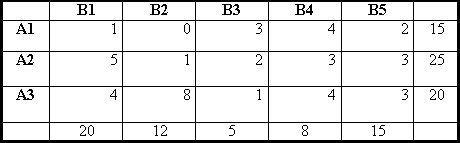
Построение опорного плана.
Находим в таблице наименьшую стоимость перевозки - это 0. Записываем в этой клетке значение 12 (наименьшее из сумм по строке и столбцу). Теперь вычеркиваем второй столбец, уменьшив сумму в первой строке на 12. Находим следующую наименьшую по стоимости ячейку - их несколько, например,11. Присваиваем ей значение3, а сумму по столбцу заменяем на 17. Вычеркиваем первую строку. Выбираем ячейку 33, присваиваем ей значение 5. сумма по третей строке равна 15 - вычеркиваем третий столбец. Выбираем ячейку 25, записываем в ней 15, уменьшаем вторую строку на 15 и вычеркиваем пятый столбец. Выбираем ячейку 31, присваиваем ей 15. Уменьшаем первый столбец на 5 и вычеркиваем третью строку. Ячейке 21 присваиваем 2.
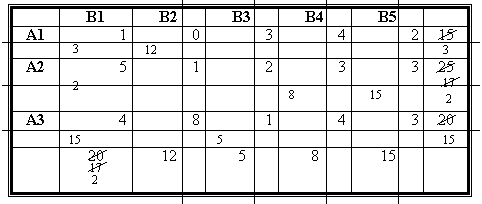
Опорный план построен.
Х11=3, Х12=12, Х21=2, Х24=8, Х25=15, Х31=15, Х33=5.
Все остальные Хij=0.
F=3*1+0*12+5*2+3*8+3*15+5*1=147
Проверим оптимальность этого плана. Для этого воспользуемся методом потенциалов.
Составим систему уравнений для нахождения потенциалов решения, найдем сумму соответствующих потенциалов для каждой свободной ячейки и пересчитаем тарифы (стоимости) для каждой свободной ячейки.
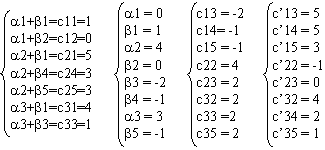
Так как у нас получились отрицательные значения, то полученный план не является оптимальным. Выберем ячейку для пересчета 22. Получим:
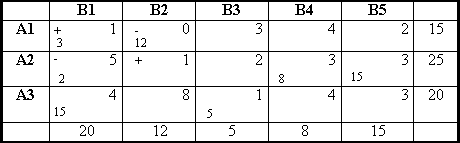
![]()
Строим следующую транспортную таблицу.
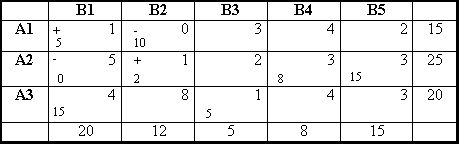
Проверим полученный план на оптимальность. Теперь ячейка 12 не заполнена.
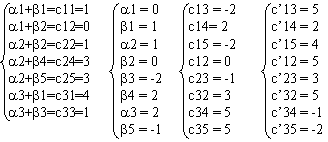
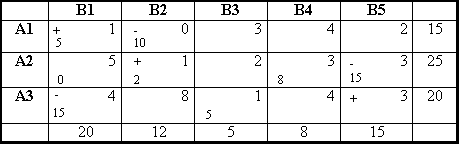
Построенный план не является оптимальным, следовательно, производим пересчет. Выберем ячейку 35.
![]()
Строим следующую транспортную таблицу.
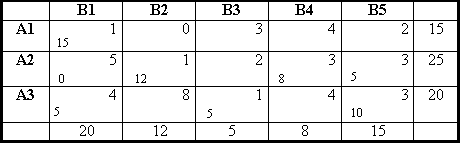
Проверим построенный план на оптимальность.
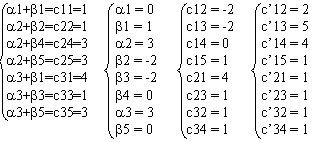
Полученный план является оптимальным. Х11=15, Х22=12, Х24=8, Х25=5, Х31=5, Х33=5, Х35=10. Все остальные Хij=0.
F=1*15+1*12+3*8+3*5+4*5+1*5+3*10=121
