Раздел: Теория оптимизации.

Линейное программирование.

Пусть - система линейных ограничений (т.е. система линейных уравнений или нестрогих линейных неравенств) с переменными , а - целевая функция вида . Задача линейного программирования формулируется следующим образом: найти при условиях . Обычно включает в себя условия неотрицательности всех переменных : - это вытекает из реального смысла чисел .

Различают две формы задач линейного программирования:

- каноническую форму, когда система ограничений состоит только из уравнений и условий неотрицательности (транспортная задача);

- стандартную форму, когда система состоит только из неравенств.

Эти две формы сводятся одна к другой введением новых или исключением некоторых переменных.

Процесс построения математической модели конкретной задачи линейного программирования включает в себя три основных этапа:

1. выбор переменных;

2. построение целевой функции;

3. учет ограничений, налагаемых на переменные.

Пример 1. Задача о банке.

Пусть собственные средства банка в сумме с депозитами составляют 100 млн. долл.

Часть этих средств, но не менее 35 млн. долл. должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно.

Другое дело ценные бумаги, которые всегда можно продать. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещенных в кредитах и ценных бумагах.

Пусть - средства, размещенные в кредитах, - средства, вложенные в ценные бумаги. Имеем следующую систему линейных ограничений:

1)

2)

3)

4) .

Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг: , где - доходность кредитов, а - доходность ценных бумаг.

Пример 2. Задача о использовании ресурсов.

Предприятие имеет в своем распоряжении определенное количество ресурсов разного рода: рабочую силу, производственные ресурсы, площади и т.п. Допустим ресурсы трех видов , имеются в количествах условных единиц. Предприятие выпускает два вида товаров . Количество единиц каждого ресурса, требуемое для производства каждого товара приведено в таблице:

Доход, получаемый предприятием от единицы товара соответственно равен и условным денежным единицам. Требуется при данных ресурсах выпустить такую комбинацию товаров, при которой доход предприятия оказался бы максимальным.

Пусть и количества товаров , тогда доход предприятия .

Общее количество ресурса , используемое при выпуске обоих товаров, равное , не должно превосходить , т.е. должны выполняться неравенства .

Математическая задача об использовании ресурсов состоит в отыскании значений неизвестных и , удовлетворяющих условиям:

и максимизирующих функцию .

Графическое решение задачи линейного программирования.

Пример 2. Графическое решение задачи о банке:

1)

2)

3)

4) .

Построим в плоскости полуплоскости заданные неравенствами 1)-4) – область допустимых решений. Для этого заменим неравенства равенствами и определим для каждого ограничения допустимую полуплоскость. Построим вектор и прямую уровня, перпендикулярную вектору и проходящую через начало координат. Перемещая эту прямую параллельно в направлении вектора , найдем последнюю точку пересечения прямой уровня и допустимого множества решений. (см. рисунок 1)

Найденная точка максимума находится на пересечении прямых 1 и 3. Ее координаты получаются решением следующей системы линейных уравнений:

Оптимальный портфель активов (максимум прибыли) имеет структуру . Максимальная прибыль составит

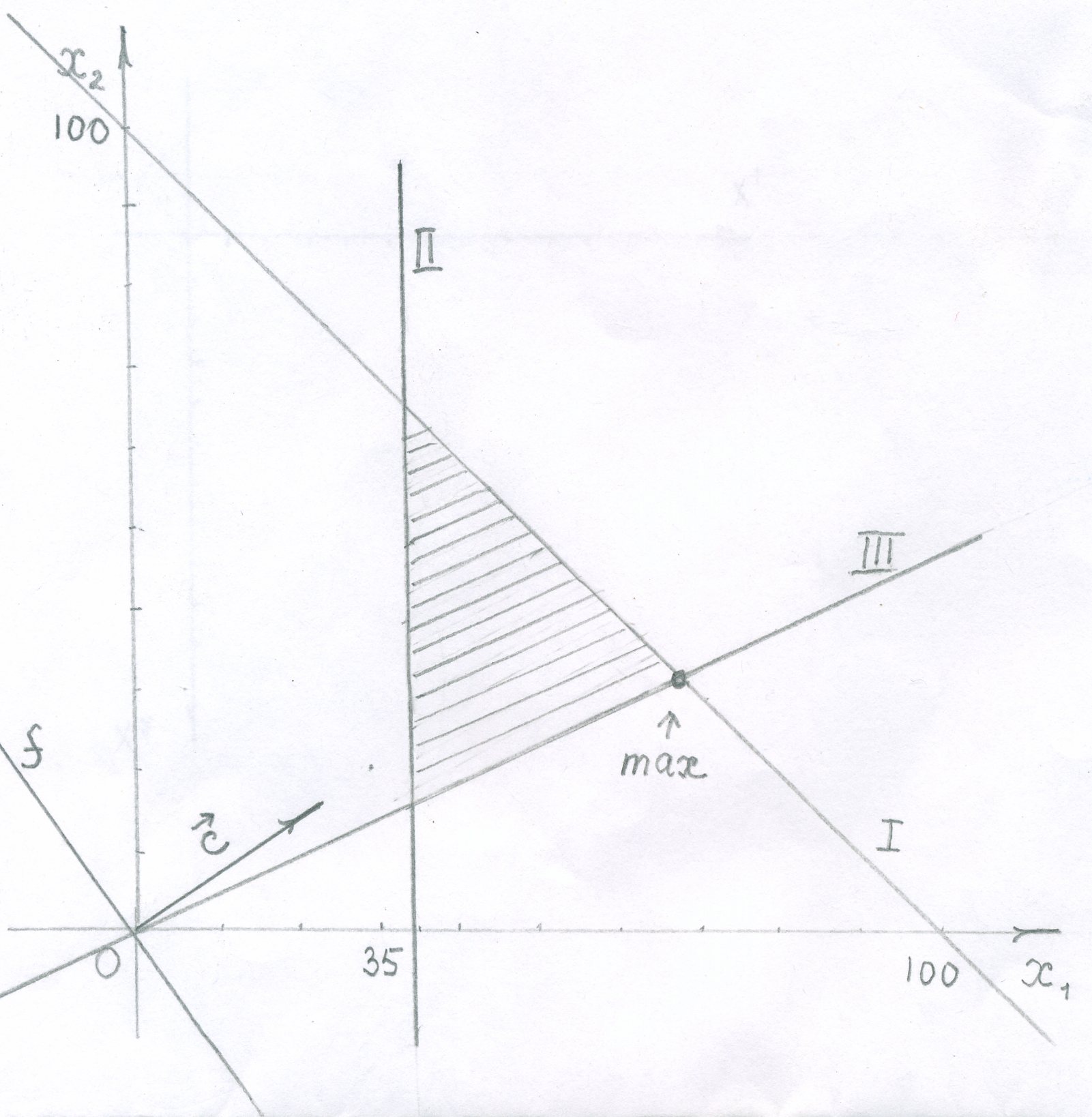
Рис. 1

Пример 2.

Для изготовления двух видов изделий А и В предприятие имеет 96 единиц сырья, причем на изготовление изделия А расходуется 8 единиц, а на В – 6 единиц сырья. Прибыль от реализации изделия А – 4 у.е., а от В 5 у.е. Определить план производства изделий, который обеспечит наибольшую прибыль от их реализации, если требуется изготовить не более 9 изделий А и не более 12 изделий В.

Решение.

Запишем математическую формулировку задачи:

1)

2)

3)

4) .

Построим в плоскости полуплоскости заданные неравенствами 1)-4) – область допустимых решений. Для этого заменим неравенства равенствами и определим для каждого ограничения допустимую полуплоскость.

Построим вектор нормали к линиям уровня целевой функции и прямую уровня, перпендикулярную вектору и проходящую через начало координат. Перемещая эту прямую параллельно в направлении вектора , найдем последнюю точку пересечения прямой уровня и допустимого множества решений. Эта точка является пересечением прямых 1 и 3. Найдем ее координаты: . Максимальное значение целевой функции соответствует ее значению в этой точке . (рис.2)

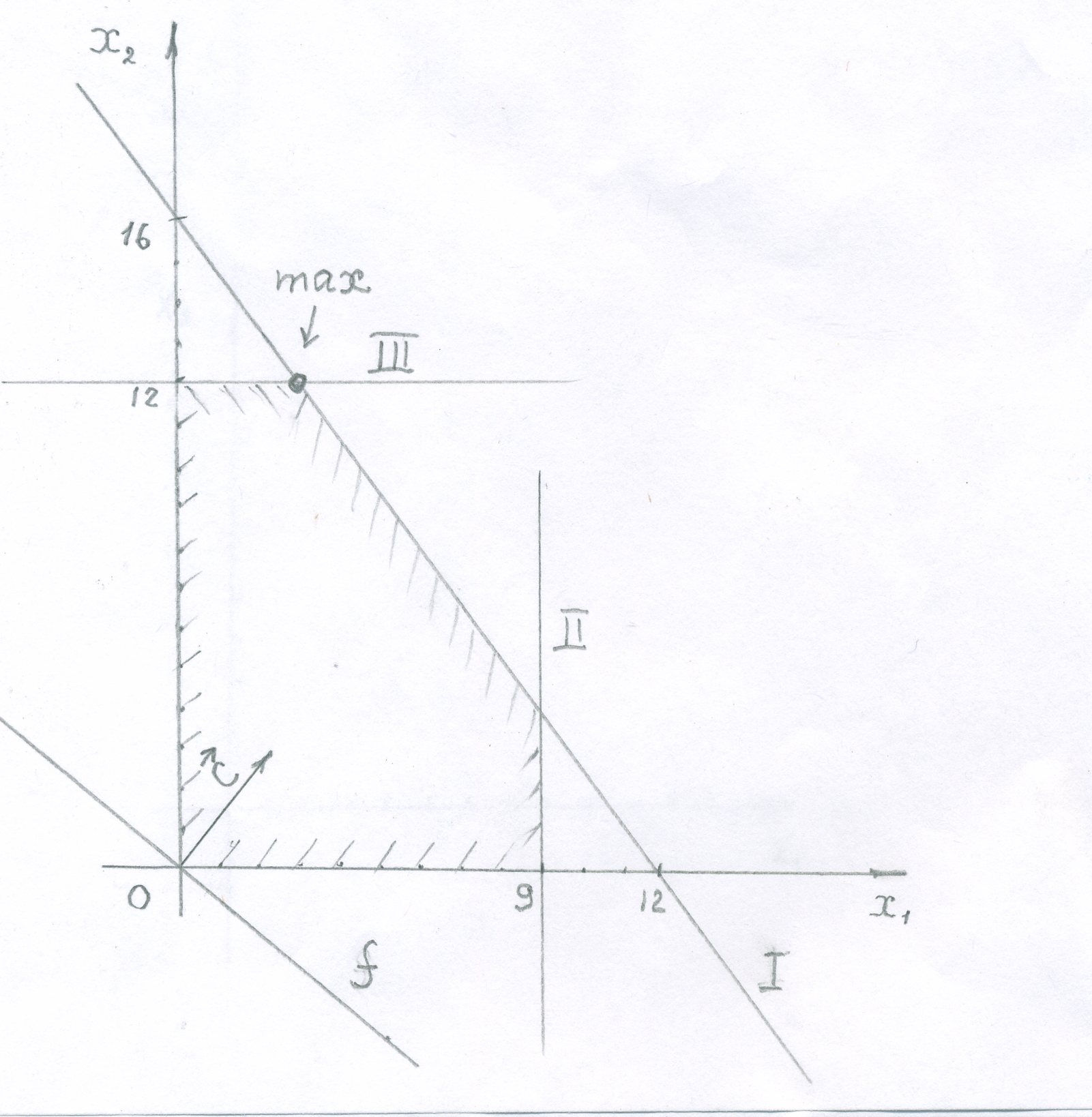
Рис. 2

Задачи для самостоятельного решения.

1. Задача о ресурсах. Для изготовления двух видов продукции используется три вида ресурсов. Запасы ресурсов, количество единиц ресурсов, используемое при изготовлении единицы продукции и величина прибыли, получаемой от продажи единицы продукции, приведены в таблице:

Вид ресурсов	Количество ресурса, необходимое для производства единицы продукта		Запасы ресурсов
	Продукт 1	Продукт 2
рабочая сила	2	5	20
материалы	8	5	40
деньги	5	6	30
Прибыль от ед. продукта	50	40

Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.

2. Задача о диете. Из имеющихся в нашем распоряжении двух продуктов составить такую диету, которая с одной стороны, удовлетворяет минимальные потребности организма в питательных веществах (белки, жиры, углеводы), с другой – требует наименьших затрат. Исходные данные приведены в таблице:

Питательные вещества	Содержание веществ в единице продукта		Суточная потребность в веществе
	Продукт 1	Продукт 2
белки	3	1	9
жиры	1	2	8
углеводы	1	6	12
Стоимость продукта	4	6	-

Записать задачу в форме задачи линейного программирования и решить ее графическим способом.

Табличный симплекс-метод.

Основная идея симплекс метода состоит в последовательном переходе от одного допустимого базиса к другому таким образом, чтобы значение целевой функции возрастало (убывало).

Пусть в записи задачи ЛП в канонической форме имеется m нетривиальных ограничений, в которые входят n неизвестных. В общем случае можно выразить m переменных через оставшиеся n-m. Переменные x1, x2,….xm – называются базисными, а x_m+1, x_m+2,….. x_n, - свободными. В простейшем случае в качестве базисных переменных можно взять m переменных, каждая из которых входит только в одно ограничение, причем с положительным знаком, а все b_i>0. За начальный (опорный) план выбирается X=(B₁, B₂,…. B_m,0,0,…0).

Алгоритм симплекс-метода .

1. Привести задачу к канонической форме (для этого в ограничения, задаваемые неравенствами ввести новые положительные переменные).

2. Определить свободные и базисные переменные.

3. Выразить целевую функцию через свободные переменные.

4. Построить симплекс-таблицу, соответствующую начальному опорному плану.

5. Проверить решение на оптимальность: если в F строке все с_j>0 (в задаче на поиск минимума - все с_i<0), то решение оптимально. Если существует с_j<0, то решение можно улучшить, введя в базис соответствующую переменную, но предварительно нужно проверить существование решения.

6. Проверка существования решения: рассматриваем столбцы, у которых с_j<0; если существует хотя бы один столбец, у которого все коэффициенты А_i,j<0, то задача решения не имеет, так как допустимое множество решений не ограничено. Если таких столбцов нет, переходим к следующему этапу.

7. Выбрать свободную переменную, которую нужно ввести в базис (выбор разрешающего столбца): это переменная, соответствующая столбцу с минимальным с_j<0.

8. Выбрать базисную переменную, которую надо вывести из базиса (выбор разрешающей строки):рассмотрим разрешающий столбец j и все его элементы, большие нуля; для всех таких элементов вычислим соотношение В_i/ A_i,j и выберем строку, для которой это соотношение минимально. Соответствующую этой строке переменную выводим из базиса. Элемент на пересечении разрешающего столбца и этой строки называется разрешающим.

9. Пересчитать симплекс-таблицу для нового базиса: делим разрешающую строку на разрешающий элемент и запишем на место разрешающей строки в новой таблице; заполняем оставшиеся строки. Для этого разрешающую строку умножаем последовательно на такие числа, чтобы после ее сложения с каждой строкой старой таблицы в разрешающем столбце получить 0 (нули в этом столбце будут везде, кроме разрешающего элемента, который будет равен 1).

10. Переходим к шагу 5.

Конец работы алгоритма:

Либо когда в F строке все элементы больше нуля, тогда оптимальное решение найдено (это столбец В последней таблицы), либо когда существует столбец, у которого все с_j<0 и все А_i,j<0. В этом случае оптимальное решение отсутствует.

Вид симплекс-таблицы.

Базис	В	x1	x2	…..	xn
X1	B1	A11	A12	…..	A1n
X2	B2	A21	A22	…..	A2n
…..	…..	…..	…..	…..	…..
Хm	Bm	Am1	Am1	…..	Ann
F	Fmax	Δ1	Δ2	…..	Δn

Пример 1. Решить задачу ЛП:

Решение.

1.Приведем задачу к канонической форме, добавив новые положительные переменные к левым частям ограничений:

2-3. Выберем базис , каждому нетривиальному ограничению в нем соответствует одна переменная. F содержит только свободные переменные, ее преобразовывать не надо.

4. Составляем начальную симплекс-таблицу.

базис	В	X1	X2	X3	X4	X5	X6	B/Ai
X4	360	18	15	12	1	0	0	360/12=30
X5	192	6	4	8	0	1	0	192/6=24 min
X6	180	5	3	3	0	0	1	180/3=60
F	0	-9	-10	-16	0	0	0

Здесь столбец В – значения правых частей ограничений, столбцы X₁… X₆- коэффициенты при неизвестных в левых частях ограничений. Чтобы получить строку F мы приравняли нулю целевую функцию и представили ее в том же виде, что и ограничения: .

5. За разрешающий столбец принимаем столбец X₃, т.к. он имеет самое минимальное отрицательное значение в строке F. Т.е. в базис будем вводить X₃.

6. За разрешающую строку принимаем строку X_5, так как для этой строки соотношение B/A₃ минимально, т.е. из базиса будем выводить X₅.

7. Переходим к новой таблице c помощью линейных преобразований строк, выбранных таким образом, чтобы получить в столбце X₃ нулевые значения везде, кроме разрешающего элемента, который должен быть равен 1 (все манипуляции производим с разрешающей строкой: ее умножаем последовательно на соответствующие числа и добавляем (отнимаем) к соответствующим строкам предыдущей таблицы!):

базис	В	X1	X2	X3	X4	X5	X6	B/Ai
X4	72	9	9	0	1	-3/2	0	72/9=8 min
X3	24	3/4	1/2	1	0	1/8	0	24/0,5=48
X6	108	11/4	3/2	0	0	-3/8	1	108/1.5=72
F	384	3	-2	0	0	2	0

Так как в строке F по-прежнему осталось отрицательное число, оптимальное решение не достигнуто. Следовательно, необходимо повторить п.п. 5-7 еще раз:

Теперь за разрешающий столбец принимаем X₂, за разрешающую строку X₄ и пересчитываем симплекс-таблицу в новом базисе:

базис	В	X1	X2	X3	X4	X5	X6	B/Ai
X2	8	1	1	0	1/9	-1/6	0	72/9=8 min
X3	20	1/4	0	1	-1/18	5/8	0	24/0,5=48
X6	96	5/4	0	0	-1/6	-1/8	1	108/1.5=72
F	400	5	0	0	2/9	5/3	0

В этой таблице нет отрицательных элементов в строке F, следовательно мы достигли оптимального решения. Это решение содержится в столбце В последней таблицы:

F_max(X₁=0, X₂=8, X3=20)=400.

Пример 2.

Предприятие производит продукцию четырех видов. Матрица затрат ресурсов на единицу продукции имеет вид:

Вектор запасов ресурсов В=(180; 150; 140), вектор цен С=(36; 30; 16; 12). Требуется найти производственную программу, максимизирующую прибыль предприятия.

Решение. Запишем математическую формулировку задачи:

Проиведем к какнонической форме, добавив в каждое неравенство дополнительное неотрицательное неизвестное:

2-3. Выберем базис , каждому нетривиальному ограничению в нем соответствует одна переменная. F содержит только свободные переменные, ее преобразовывать не надо.

4. Составляем начальную симплекс-таблицу.

базис	В	X1	X2	X3	X4	X5	X6	X7	B/Ai
X5	180	4	5	2	3	1	0	0	180/4=45
X6	150	6	0	4	1	0	1	0	150/6=25 min
X7	140	0	7	6	5	0	0	1	180/3=60
F	0	-36	-30	-16	-12	0	0	0

5. За разрешающий столбец принимаем столбец X₁, т.к. он имеет самое минимальное отрицательное значение в строке F. Т.е. в базис будем вводить X₁.

6. За разрешающую строку принимаем строку X_6, так как для этой строки соотношение B/A₁ минимально, т.е. из базиса будем выводить X₆.

7. Переходим к новой таблице c помощью линейных преобразований строк, выбранных таким образом, чтобы получить в столбце X₁ нулевые значения везде, кроме разрешающего элемента, который должен быть равен 1 (все манипуляции производим с разрешающей строкой: ее умножаем последовательно на соответствующие числа и добавляем (отнимаем) к соответствующим строкам предыдущей таблицы!):

базис	В	X1	X2	X3	X4	X5	X6	X7	B/Ai
X5	80	0	5	-2/3	7/3	1	-2/3	0	80/5=16 min
X1	25	1	0	2/3	1/6	0	1/6	0
X7	140	0	7	6	5	0	0	1	140/7=20
F	900	0	-30	8	-6	0	6	0

Так как в строке F по-прежнему осталось отрицательное число, оптимальное решение не достигнуто. Следовательно, необходимо повторить п.п. 5-7 еще раз:

За разрешающий столбец принимаем столбец X₂, т.к. он имеет самое минимальное отрицательное значение в строке F. Т.е. в базис будем вводить X₂.

За разрешающую строку принимаем строку X_5, так как для этой строки соотношение B/A₁ минимально, т.е. из базиса будем выводить X₅.

Переходим к новой таблице:

базис	В	X1	X2	X3	X4	X5	X6	X7	B/Ai
X2	16	0	1	-2/15	7/15	1/15	-2/15	0
X1	25	1	0	2/3	1/6	0	1/6	0
X7	28	0	0	104/15	26/15	-7/15	14/15	1
F	1380	0	0	4	8	6	2	0

В строке F не осталось отрицательных элементов, следовательно, на этом шаге мы получили оптимальное решение. Это решение находится в столбце В последней таблицы:

F_max(X₁=25, X₂=16, X3=0)=1380. Таким образом оптимальная производственная программа заключается в выпуске 25 ед. первого продукта и 16 ед. второго. Продукция третьего и четвертого типов не выпускается. Остаток ресурсов третьего вида – 28 ед. Максимальная прибыль предприятия – Z_мах = 1380 ден. ед.