
- •Электричество и магнетизм
- •4. Основные формулы Электромагнетизм
- •4.1. Примеры решения задач
- •6.4. Удельное сопротивление проводников (при 00 с), мкОмм
- •3. Основные формулы. Оптика Преломление света
- •Интерференция света
- •Дифракция света
- •Поляризация света
- •Законы теплового излучения
- •Фотоэлектрический эффект
- •Давление света. Фотоны
- •Эффект Комптона
- •Теория относительности
- •4. Основные формулы. Атомная физика Атом водорода
- •Волны де Бройля
- •Радиоактивность
- •Энергия связи атомных ядер
- •Ядерные реакции
- •4.1. Примеры решения задач
- •В нерелятивистском случае
- •Вопросы для подготовки к экзамену
- •Периоды полураспада радиоактивных изотопов
- •Массы изотопов, а.Е.М.
В нерелятивистском случае
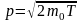 ,
(2)
,
(2)
где m0 – масса покоя частицы.
В релятивистском случае
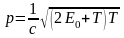 ,
(3)
,
(3)
где Е0 = m0с2 – энергия покоя частицы.
Формула (1) с учетом соотношений (2) и (3) запишется:
в нерелятивистском случае
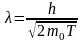 ,
(4)
,
(4)
в релятивистском случае
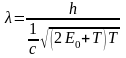 .
(5)
.
(5)
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1 = 51 В и U2 = 510 кВ, с энергией покоя электрона и в зависимости от этого решим, которую из формул (4) или (5) следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона Т, прошедшего ускоряющую разность потенциалов U, Т=eU.
В
первом случае Т1
= eU1
= 51 эВ = 0, 5110-4
МэВ, что много меньше энергии покоя
электрона Е0
= m0с2
= 0, 51 МэВ.
Следовательно, в этом случае можно
применить формулу (4). Для упрощения
расчетов заметим, что Т1=
10-4
m0с2.
Подставив это выражение в формулу (4),
перепишем ее в виде
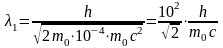 .
.
Учитывая,
что
есть комптоновская длина волны ,
получим
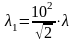 .
Так как
= 2, 43 пм, то
.
Так как
= 2, 43 пм, то
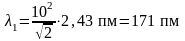 .
.
Во втором случае кинетическая энергия Т2 = eU2 = 510 кэВ = 0, 51 МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что Т2 = 0, 51 МэВ = m0с2, по формуле (5) найдем
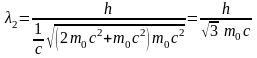 ,
или
,
или
 .
.
№ 3. Кинетическая энергия электрона в атоме водорода составляет величину порядка T = 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
Р е ш е н и е.
Соотношение
неопределенностей для координаты и
импульса имеет вид
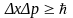 ,
где x
– неопределенность координаты частицы
(в данном случае электрона); р
– неопределенность импульса частицы
(электрона);
,
где x
– неопределенность координаты частицы
(в данном случае электрона); р
– неопределенность импульса частицы
(электрона);
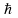 – постоянная Планка, деленная на 2.
– постоянная Планка, деленная на 2.
Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а, следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где –то в пределах области с неопределенностью
Δх = l/2 . (1)
Соотношение
неопределенностей (1) можно записать в
этом случае в виде
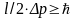 ,
откуда
,
откуда
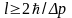 .
(2)
.
(2)
Физически разумная неопределенность импульса р во всяком случае не должна превышать значения самого импульса р, т.е. р р.
Импульс
р
связан с кинетической энергией Т
соотношением
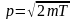 .
Заменим р
на
.
Заменим р
на
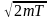 (такая
замена не увеличит l).
Переходя от неравенства к равенству,
получим
(такая
замена не увеличит l).
Переходя от неравенства к равенству,
получим
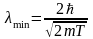 .
.
Подставим числовые значения и произведем вычисления:
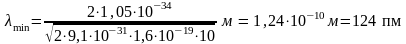 .
.
№ 4.
Вычислить дефект массы и энергию связи
ядра
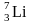 .
.
Р е ш е н и е.
Масса ядра всегда меньше суммы масс свободных (находящихся вне ядра) протонов и нейтронов, из которых ядро образовалось. Дефект массы ядра m и есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е.
 ,
(1)
,
(1)
где Z – атомный номер (число протонов в ядре); А – массовое число (число нуклонов в ядре); mр, mn, m – соответственно, массы протона, нейтрона и ядра.
В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в нее входила масса М нейтрального атома. Можно считать, что масса нейтрального атома равна сумме масс ядра и электронов, составляющих нейтральную оболочку атома: М = m+Zme , откуда m = М - Zme.
Выразив в равенстве (1) массу ядра по последней формуле, получим Δm = Ζmp+ (A – Ζ)mn – M +Ζme, или Δm = Ζ(mp +me) + (A – Ζ)mn – M.
Замечая, что mе + mp = MH, где MH – масса атома водорода, окончательно получим
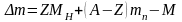 .
(2)
.
(2)
Подставив в выражение (2) числовые значения масс (из справочных таблиц), получим
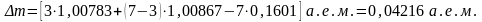
Энергией связи Е ядра называется энергия, которая в той или иной форме выделяется при образовании ядра из свободных нуклонов.
В соответствии с соотношением пропорциональности массы и энергии
Е = с2m, (3)
или с2 = Е /m = 91016 Дж/кг. Если вычислить энергию связи, пользуясь внесистемными единицами, то с2 = 931 МэВ/а.е.м. С учетом этого формула (3) примет вид
Е = 931 m (МэВ). (4)
Подставив ранее найденное значение дефекта массы ядра в формулу (4), получим
Е = 9310,04216 МэВ = 39,2 МэВ.
№ 5.
При соударении
– частицы
с ядром бора
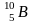 произошла ядерная реакция, в результате
которой образовалось два новых ядра.
Одно из них – ядро атома водорода
произошла ядерная реакция, в результате
которой образовалось два новых ядра.
Одно из них – ядро атома водорода
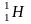 .
Определить порядковый номер и массовое
число второго ядра, дать символическую
запись ядерной реакции и определить ее
энергетический эффект.
.
Определить порядковый номер и массовое
число второго ядра, дать символическую
запись ядерной реакции и определить ее
энергетический эффект.
Р е ш е н и е.
Обозначим
неизвестное ядро символом
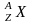 .
Так как
– частица
представляет собой ядро гелия
.
Так как
– частица
представляет собой ядро гелия
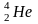 ,
запись реакции имеет вид
,
запись реакции имеет вид
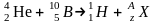 .
.
Применив закон сохранения числа нуклонов, получим уравнение
4 +10 = 1 + А, откуда А = 13. Применив закон сохранения заряда, получим уравнение 2 + 5 = 1 +Z, откуда Z = 6.
Следовательно,
неизвестное ядро является ядром изотопа
атома углерода
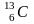 .
.
Энергетический эффект Q ядерной реакции определяется по формуле Q = 931 [(mHe+ mB) – ( mH + mC)]. Здесь в первых круглых скобках указаны массы исходных ядер, во вторых скобках – массы ядер – продуктов реакции. При числовых подсчетах по этой формуле массы ядер заменяют массами нейтральных атомов. Возможность такой замены вытекает из следующих соображений.
Число электронов в электронной оболочке нейтрального атома равно его зарядовому числу Z. Сумма зарядовых чисел исходных ядер равна сумме зарядовых чисел ядер – продуктов реакции. Следовательно, электронные оболочки ядер гелия и бора содержат вместе столько же электронов, сколько их содержат электронные оболочки ядер углерода и водорода.
Очевидно, что при вычитании суммы масс нейтральных атомов углерода и водорода из суммы масс атомов гелия и бора массы электронов выпадут, и мы получим тот же результат, как если бы брали массы ядер. Подставив массы атомов, взятые из справочной таблицы в расчетную формулу, получим
Q = 931 [(4,00260+10,01294)-(1,00783+13,00335)] Мэв = 4,06 МэВ.
№ 6. Определить начальную активность радиоактивного препарата магния 27Mg массой m = 0,2 мкг, а также его активность А через время t = 6 ч. Период полураспада T1/2 магния считать известным.
Р е ш е н и е.
Активность
А
изотопа характеризует скорость
радиоактивного распада и равняется
числу ядер, распадающихся в единицу
времени:
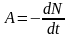 ,
где dN – число
ядер, распавшихся за время dt.
,
где dN – число
ядер, распавшихся за время dt.
Согласно
основному закону радиоактивного распада
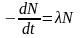 ,
где
– постоянная радиоактивного распада.
Так как
,
где
– постоянная радиоактивного распада.
Так как
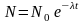 ,
где N0
– число не распавшихся ядер в момент
времени, принятый за начальный, то
,
где N0
– число не распавшихся ядер в момент
времени, принятый за начальный, то
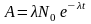 .
.
Очевидно, что начальная активность при t = 0
А0 = N0 . (1)
Поэтому закон изменения активности со временем выражается формулой
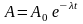 .
(2)
.
(2)
Начальную активность определим по формуле (1). Входящая в эту формулу постоянная радиоактивного распада может быть выражена через период полураспада соотношением = ln 2/T1/2 = 0,693/T1/2.
Для 27Mg период полураспада T1/2 = 10 мин = 600 с. Следовательно, = 0,693/600 с-1 = 1,1510-3 с-1.
Число
радиоактивных атомов N0,
содержащихся в изотопе, равно произведению
числа Авогадро NA
на количество
вещества
данного изотопа:
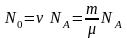 ,
где m
– масса изотопа;
– молярная масса. Выразив в этой формуле
значения величин в системе Си, получим
,
где m
– масса изотопа;
– молярная масса. Выразив в этой формуле
значения величин в системе Си, получим
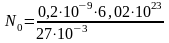 ядер = 4,461015
ядер.
ядер = 4,461015
ядер.
Вычислим по формуле (1) начальную активность изотопа: А0 = N0 = 1,1510-34,461015 Бк = 5,131012 Бк. Или А0 = 5,13 ТБк.
Активность
через 6 ч (6ч = 2,16104
с) получим по формуле (2):
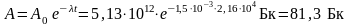 .
.
№ 7. Космическое излучение на уровне моря на экваторе образует в воздухе объемом V = 1 см3 в среднем N = 24 пары ионов за время t1 = 10 c. Определить экспозиционную дозу X, получаемую человеком за время t2 = 1 год.
Р е ш е н и е.
Экспозиционную дозу, получаемую человеком, можно выразить формулой
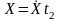 ,
(1)
,
(1)
где X – мощность экспозиционной дозы излучения.
Мощность
дозы
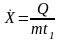 ,
где Q – заряд
ионов одного знака, образуемых излучением
за время t1
в воздухе массой m.
Масса m
= V.
Заряд всех ионов одного знака найдем,
умножив элементарный заряд на число
ионов: Q =eN.
,
где Q – заряд
ионов одного знака, образуемых излучением
за время t1
в воздухе массой m.
Масса m
= V.
Заряд всех ионов одного знака найдем,
умножив элементарный заряд на число
ионов: Q =eN.
Формула
(1) с учетом выражений для
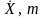 и
Q примет
вид
и
Q примет
вид
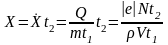 .
Выразим величины, входящие в формулу
(2), в единицах СИ и, выполнив вычисления,
получим: X
= 9,41 мкКл/кг.
.
Выразим величины, входящие в формулу
(2), в единицах СИ и, выполнив вычисления,
получим: X
= 9,41 мкКл/кг.
КОНТРОЛЬНЫЕ ЗАДАЧИ ПО АТОМНОЙ ФИЗИКЕ
1 Определить наибольшую и наименьшую длины волн в первой инфракрасной серии водорода (Серия Пашена).
2. Электрон движется по окружности радиусом 0,5 см в однородном магнитном поле с индукцией 8 мТл. Определить длину волны де Бройля электрона.
.
3. За один год начальное количество радиоактивного нуклида уменьшилось в 3 раза. Во сколько раз оно уменьшится за 2 года?
4.
Во сколько раз отличается удельная
энергия связи (энергия связи, рассчитанная
на один нуклон) для ядер
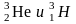 ?
?
5. Вычислить энергию ядерной реакции в МэВ:
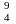 Be
+
Be
+
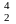 He
→
He
→
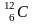 +
+
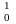 n.
n.
6. Какой порядковый номер в таблице Менделеева имеет элемент, который образуется в результате излучения γ – кванта ядром элемента с порядковым номером Z?
