2.6. Зуборезные долбяки

По конструкции долбяки представляют собой цилиндрические корригированные зубчатые колеса – прямозубые или косозубые, обращенные в режущий инструмент путем придания их зубьям передних, боковых и задних углов.

Долбяки работают по методу обкатки. В процессе зубодолбления независимо от того, прямозубое или косозубое колесо, ось долбяка всегда параллельна оси колеса.

Поэтому при нарезании косых зубьев, долбяк косозубый, прямых – прямозубый, причем наклон зубьев долбяка является противоположным наклону зубьев колеса наружного зацепления и совпадает – для внутреннего зацепления.

Основная область применения долбяков – нарезание зубьев у колес внутреннего зацепления, блочных, шевронных и т.д., для которых использование червячных зуборезных фрез невозможно, а также для колес с малым числом зубьев.

Зубодолбление обеспечивает более высокую точность и шероховатость обработанной поверхности, но меньшую производительность нарезания.

Хвостовые долбяки применяют для нарезания колес внутреннего зацепления.

Чашечные долбяки – для колес блочного типа.

Для шевронных колес используют комплект из двух долбяков, сидящих на одной оправке, но имеющих противоположные наклоны зубьев.

2.6.1. Эвольвентное зацепление

Для уяснения понятий правильности зацепления, рассмотрим вопрос получения эвольвентного профиля в процессе обкатки.

Из большого числа винтовых поверхностей, образуемых путем винтового движения прямой или кривой линии вокруг оси.

Практический интерес представляет открытая эвольвентная винтовая поверхность.

При этом образующая прямая все время остается касательной к цилиндрической поверхности, называемой направляющим (основным) цилиндром.

Эвольвента (рис. 2.46) – кривая АА₁, образованная любой точкой Х производящей прямой, катящейся без скольжения по окружности радиуса r_в, называемой основной. Точка же А₂ касания производящей прямой с основной окружностью, представляет собой мгновенный центр вращения прямой и одновременно центр кривизны эвольвенты.

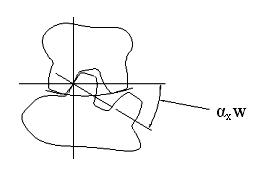
Рис. 2.45. Эвольвентное зацепление

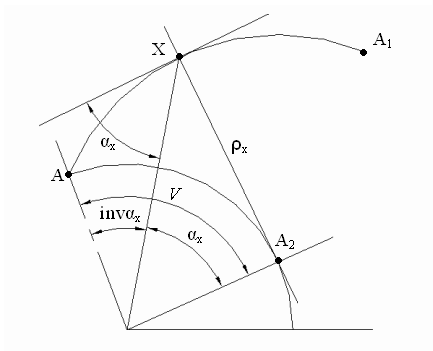
Рис. 2.46. Эвольвента

Отрезок А₂Х производящей прямой является нормалью к эвольвенте в заданной точке Х и одновременно радиусом кривизны ρ_х этой кривой.

Эвольвентный, или полярный, угол invα_х заключен между радиус-векторами в начальной А и рассматриваемой точке эвольвенты и характеризует положение точки Х на эвольвенте.

Угол между радиальными лучами к рассматриваемой точке эвольвенты Х и точке А₂ – является углом давления α_х.

Если точка Х лежит на начальной окружности, угол давления равен углу зацепления α_tw. Сумма углов α_х и invα_х называется углом развернутости эвольвенты зуба в данной точке Х, т.е. углом, заключающим крайние точки

развернутой дуги основной окружности:

V = invα_x + α_x.

Исходя из сказанного, можно написать следующие зависимости:

ρ_х = UAA₂ = r_в(invα_x + α_x) ; ρ_х = tgα_x ,

откуда

r_в(invα_x + α_x)= tgα_x ,

следовательно, полярный угол точки Х эвольвенты, выражается уравнением эвольвенты:

invα_x= tgα_x - α_x , рад.

Обеспечение правильности зацепления обработанных зубчатых колес, основывается на положении, что активный профиль зубьев этих колес должен быть меньше активного профиля зубьев при зацеплении их с долбяком.

Кривая реальной проекции передней поверхности зуба долбяка не является точной эвольвентой, то для определения толщины зуба S_x на любом диаметре D_x используют формулу геометрии эвольвенты:

,

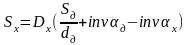а в исходном сечении:

,

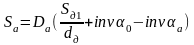где α_д и α_а - углы давления по делительной окружности и вершине зуба, соответственно.