
- •Модуль 1. Естественнонаучные основы представлений об окружающей действительности
- •Тема 3. Основы концепций представления организации материи Лабораторная работа № 3
- •1.1.1. Цели работы
- •1.2.2. Самостоятельная работа студентов
- •1.1.3. Средства и способы проведения эксперимента
- •1.4.4. Порядок выполнения работы
Модуль 1. Естественнонаучные основы представлений об окружающей действительности
Тема 3. Основы концепций представления организации материи Лабораторная работа № 3
Использование компьютерного моделирования для представления и оценки скалярных и векторных полей
1.1.1. Цели работы
1. Создание целостного научного представления об окружающем пространстве при взгляде на него с точки зрения того, что в нем действуют электрические, магнитные, гравитационные и другие поля.
2. Сформировать необходимый для будущей профессии набор различных видов деятельности по компьютерному моделированию и визуализации с помощью компьютерной графики различных полей.
3. Сформировать базовые компетенции обнаруживать в природе, технике, быту изучаемые понятия о полевом устройстве окружающего мира, применять современный научный аппарат естествознания, используемый для характеристики полей.
4. Сформировать базовые компетенции оперировать фактами, получаемыми посредством средств измерений, чувств человека, а также визуализируемых и воспринимаемых с помощью современных средств компьютерного моделирования и компьютерной графики
5. Сформировать простейшие компетенции применять для извлечения требуемой информации о структуре и характеристиках полей справочники, научно – техническую литературу, Internet
6. Путем решения заданий и анализа их результатов выработать умения практического использования типовых программных продуктов для оперирования численной информацией при различных способах ее представления.
1.2.2. Самостоятельная работа студентов
Перед выполнением лабораторной работы студенту необходимо:
1. Повторить основные понятия, связанные электрическими, магнитными, гидродинамическими и газодинамическими полями.
2. Вспомнить, а в случае необходимости повторно изучить такие понятия заряд, ток.
3. Провести самопроверку эффективности своей теоретической подготовки, ответив на вопросы, приведенные в разделе «Контрольные вопросы».
4. Изучить эксперименты, описания всех способов обработки информации. В результате исполнения этого пункта студент должен уметь объяснять порядок выполнения работы и то, какие результаты он ожидает получить.
5. Подготовить отчет о лабораторной работе.
Надо помнить, что таблицы, результаты исследований помещаются в электронном документе отдельно по каждому пункту задания.
1.1.3. Средства и способы проведения эксперимента
В лабораторной работе экспериментальные исследования выполняется на IBM PC с использованием пакетов программ MATLAB.
1.4.4. Порядок выполнения работы
Мы в предыдущих лабораторных работах определенно придерживались «механистического» взгляда на мир. Вспомните, что мы все объясняли посредством подхода, в основе которого лежал принцип «тяни-толкай».
Представьте, что перед нами вертикальный металлический прут, привязанный вверху к закрепленной бечевке. Если прут толкнуть пальцем или потянуть его за нижний конец (то есть, как мы говорили, к нему приложить силу), то прут начнет двигаться и менять свое пространственное положение. Причем в этом случае силы (толчок или тяга) проявляются, только при касании тела. Когда Вы толкаете прут, то его касается ваш палец. Можно конечно сдвинуть прут вроде бы не касаясь: просто подув на него. Но и в этом случае имеет место «толкание», поскольку дуя, вы толкаете в направлении прута молекулы воздуха и те, касаясь его, толкают прут.
Три закона механики Ньютона объясняли действие этих сил. Эти законы же могут быть применены для объяснения принципов действия большого числа разнообразных машин, в которых рабочие органы толкают и тянут друг друга и, тем самым (посредством приложения сил), действуют на рычаги, шкивы, шестерни, колеса. В таких машинах для совершения механической работы одни тела прилагают силу к другим телам, касаясь друг друга.
Итак, механистический взгляд на Вселенную предполагает, что все движется благодаря касанию и приложению сил.
А может ли существовать силы без контакта или касания. Да могут.
Известно, что Земля притягивает Луну и удерживает ее на орбите, без касания. При этом между этими двумя телами нет абсолютно ничего, даже воздуха. В школе Вам это явление объясняли тем, что между Землей и Луной есть так называемая сила гравитации.
Можно наблюдать еще одну силу, не требующую контакта. Если Вы возьмете магнит, то приблизив его к нижнему концу железного прута, Вы обнаружите, что он без всякого контакта наклоняется в сторону магнита. Аналогичная ситуация имеет место, если тонкому магнитику дать возможность поворачиваться на конце оси, чтобы он стал компасом. С такими компасами европейские мореплаватели начинали исследовать океаны примерно в 1350-х годах. «Загадочные» силы без всякого контакта ориентировали магнитик на север и на юг, потому что их «притягивали» далекие полярные области Земли.
В настоящее время принято разграничивать окружающие нас объекты материального мира (часто используют термин- материя) на два больших и самостоятельных класса. Один из них называют веществом, а другой – полем. В основе принципа, позволяющего проводить такое деление, лежит тот факт, что вещество в отличие от поля обладает инертной массой, центром масс и пр. в обычном механическом смысле. Движение макроскопических объектов, состоящих из вещества, описывается известными законами механики Ньютона.
Как Вам известно, большинство известных в природе веществ могут существовать в трех состояниях; газообразном, жидком и твердом, называемых агрегатными состояниями. Четвертым агрегатным состоянием нередко считают плазму – частично или полностью ионизированный при высокой температуре газ, в котором объемные плотности положительных и отрицательных зарядов примерно одинаковы.
Газ состоит из молекул и атомов, расстояния между которыми сравнительно велики, что приводит к относительно слабому взаимодействию между этими частицами и достаточно свободному движению в занимаемом ими объеме. В газообразном состоянии взаимодействие между нейтральными частицами определяется силами Ван-дер-Ваальса. Притяжение вызвано взаимной поляризацией молекул, а отталкивание частиц – соприкосновением электронных оболочек атомов, входящих в состав молекул. Энергия связи между частицами имеет порядок 102… 103 Дж/моль.
По сравнению с газообразным состоянием в жидком и твердом состояниях, молекулы и атомы расположены значительно ближе друг к другу, а энергия связи между частицами имеет порядок 107 Дж/моль.
Жидкостью называют агрегатное состояние вещества, промежуточное между газообразным и твердым состояниями: подобно газу она принимает форму заполняемого сосуда и ее свойства при отсутствии внешних воздействий обычно не зависит от направления. То есть жидкость обладает изотропией. Жидкость подобно твердому телу образует поверхность раздела с газообразной средой, обладает некоторой прочностью на разрыв. По химическому составу различают однокомпонентные (или чистые) жидкости и многокомпонентные смеси (растворы).
Твердым телом называют агрегатное состояние вещества, характеризуемое стабильностью формы и тепловым движением атомов, совершающих малые колебания относительно своих положений равновесия. Различают твердые аморфные, не имеющие точки плавления и обычно обладающие изотропией свойств, и твердые кристаллические тела. При повышении температуры вещество в аморфном состоянии размягчается и переходить в жидкое состояние постепенно, что обусловлено отсутствием у него присущей кристаллам строгой периодичности в расположении атомов, ионов, молекул и их групп в объемах, размеры которых велики по сравнению с межатомными расстояниями.
Понятие поля лежит в основе многих
представлений современного окружающего
мира. С формальной точки зрения термин
«поле» употребляется тогда, когда надо
сопоставить каждой точке пространства
некоторую физическую характеристику.
В общем случае говорят, что в пространстве
задано поле некоторой величины
![]() ,
если в каждой точке пространства (или
некоторой его части) определено значение
этой величины. По-другому, некоторой
охватывающей области пространства
присваивают некоторую функцию
,
зависящую от пространственных координат
или радиус-вектора
,
если в каждой точке пространства (или
некоторой его части) определено значение
этой величины. По-другому, некоторой
охватывающей области пространства
присваивают некоторую функцию
,
зависящую от пространственных координат
или радиус-вектора
![]() .
.
Поле величины
называется стационарным (или
установившимся), если
не зависит от времени
![]() .
В противном случае поле называется
нестационарным (неустановившемся).
Таким образом, в общем случае величина
есть функция точки
.
В противном случае поле называется
нестационарным (неустановившемся).
Таким образом, в общем случае величина
есть функция точки
![]() и времени
.
и времени
.
В реальной жизни приходится иметь дело со скалярными или векторными величинами. Соответственно, с этим различают два вида полей: скалярные и векторные. В соответствии с этим поля определяются заданием в каждой точке рассматриваемой области пространства либо некоторой скалярной (величины, характеризуемой числом) либо некоторой векторной величины (характеризуемой не только числом – модулем (длиной вектора), но и направлением в пространстве).
Пусть
![]() - некоторая область на плоскости или в
пространстве. Если каждой точке
из
определена (поставлена в соответствие)
скалярная величина (то есть число), то
говорят, что в области
задано скалярное поле. Скалярное
поле, характеризуется скалярной функцией
- некоторая область на плоскости или в
пространстве. Если каждой точке
из
определена (поставлена в соответствие)
скалярная величина (то есть число), то
говорят, что в области
задано скалярное поле. Скалярное
поле, характеризуется скалярной функцией
![]() ,
зависящей от координат пространства.
Если в пространстве ввести систему
координат
,
зависящей от координат пространства.
Если в пространстве ввести систему
координат
![]() ,
то каждая точка
в этом пространстве будет иметь
определенные координаты
,
то каждая точка
в этом пространстве будет иметь
определенные координаты
![]() и скалярная величина
будет являться функцией этих координат
и скалярная величина
будет являться функцией этих координат
![]() .
.
Как о скалярном поле можно говорить о
«поле температур»
![]() воздуха в помещении, если температуру
рассматривать как функцию точки
.
В точках, расположенных ближе к источнику
теплоты, температура выше, дальше от
источника теплоты – ниже. Если окажется,
что температура везде одинаковая, то в
этом случае скалярное поле постоянно
или однородно. В атмосфере мы имеем
дело со скалярными «полями давлений»
воздуха в помещении, если температуру
рассматривать как функцию точки
.
В точках, расположенных ближе к источнику
теплоты, температура выше, дальше от
источника теплоты – ниже. Если окажется,
что температура везде одинаковая, то в
этом случае скалярное поле постоянно
или однородно. В атмосфере мы имеем
дело со скалярными «полями давлений»
![]() ,
плотности материальной среды
,
плотности материальной среды
![]() .
При этом каждой точке пространства
ставятся в соответствие какие-то числа
(например, значения давления), зависящие
от координат (от вектора
,
проведенного в эту точку). Например,
поле давления в атмосфере
.
При этом каждой точке пространства
ставятся в соответствие какие-то числа
(например, значения давления), зависящие
от координат (от вектора
,
проведенного в эту точку). Например,
поле давления в атмосфере
![]() ,
поле плотности вещества
,
поле плотности вещества
![]() .
.
Заметим, что поле есть нечто «размазанное» в пространстве, оно не имеет инертной массы, поэтому для его описания нельзя применять механический подход.
Примером скалярного поля может служить снимок, который демонстрирует нам скалярное поле объемной плотности (то есть количества субстанции в единице объема тела, занимающего пространственную область) мерцающего в космическом пространстве водорода (гидрогенного газа) и небольшого количества других элементов, таких как кислород и сера (рис.1). Напоминающий гнев разъяренного моря, снимок, был сделан размещенным в космосе телескопом Hubble 29-30 мая 1999 года. Опубликованный в честь 13 годовщины запуска телескопа Hubble (NASA) снимок запечатлел небольшую область в очаге возникновения звезд M17. Область M17, также известная как Омега или Туманность Лебедя, находится примерно в 5 500 световых лет от созвездия Стрельца.
Световой год (св. г., ly) — внесистемная единица длины, равная расстоянию, проходимому светом за год. Иначе говоря, световой год равен: 9 460 7300 472 580, 8 километрам.

Рис. 1. Скалярное поле объемной плотности мерцающего в космическом пространстве водорода и небольшого количества других элементов, таких как кислород и сера.
Демонстрирует нам скалярное поле также снимок колонны газа и пыли (рис.2), который называется туманностью Конуса (NGC 2264) и находится в турбулентной области образования звезд.
 Рис.
2. Скалярное поле мерцающего в космическом
пространстве газа и пыли туманности
Конуса, находящейся в 2 500 световых лет
от созвездия Единорог.
Рис.
2. Скалярное поле мерцающего в космическом
пространстве газа и пыли туманности
Конуса, находящейся в 2 500 световых лет
от созвездия Единорог.
Название связано с тем, что на снимках, сделанных с земли, туманность имеет форму конуса, эта огромная колонна. Этот снимок, сделанный 2 апреля 2002 года специальной камерой для продвинутых исследований на телескопе NASA, демонстрирует верхнюю туманность «ростом» 2,5 световых лет. Вся туманность составляет 7 световых лет в длину.
Для наглядного изображения скалярного
поля следовало бы около каждой точки
написать то значение, которое в
рассматриваемой точке принимает
рассматриваемая величина. Однако
практически это неосуществимо, поэтому
пользуются иным способом: выбирают
некоторые дискретные значения
![]() ,
обычно взятые через равные интервалы,
и проводят поверхности уровня, каждая
из которых проходят через все дискретные
точки.
,
обычно взятые через равные интервалы,
и проводят поверхности уровня, каждая
из которых проходят через все дискретные
точки.
Скалярное поле
,
представляющее 3-D изображение, можно
наглядно отобразить при помощи семейства
секущих поверхностей определенного
уровня
![]() ,
где
,
где
![]() -константы.
Такие поверхности носят название
поверхностей уровня или изоповерхностей.
Если придать различные значения
,
то получим семейство поверхностей
уровня, на каждой из которых скаляр
принимает постоянное значение..
-константы.
Такие поверхности носят название
поверхностей уровня или изоповерхностей.
Если придать различные значения
,
то получим семейство поверхностей
уровня, на каждой из которых скаляр
принимает постоянное значение..
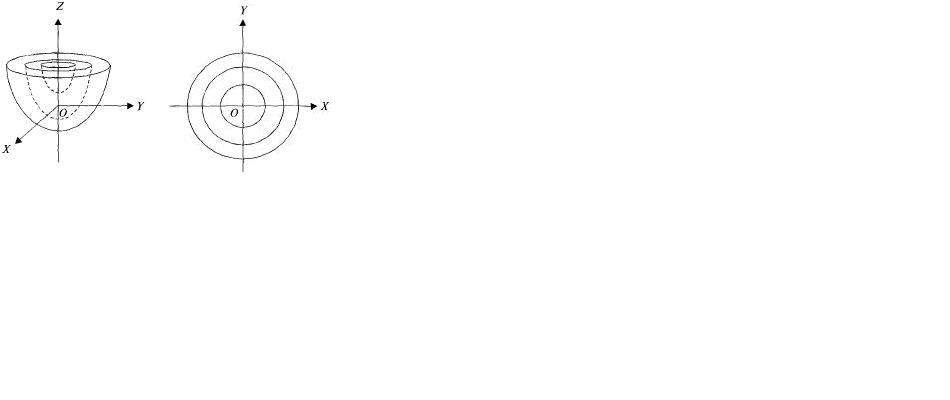
Рис. 3а. Уравнение
параболоида в трёхмерной области
определяет семейство поверхностей
уровня окружностей
![]()
Изображение функций с помощью поверхностей уровня широко применяется в метеорологии (изотермы, изобары и т.д.), геодезии и топографии (горизонтали) и других науках.
При сложных скалярных полях семейство поверхностей уровня в некоторой степени наглядно характеризует скалярное поле. Так, места сближения изоповерхностей указывают на быстрое изменение здесь функции .
Можно определить вектор, который позволяет найти быстроту изменения поля при перемещении точки в любом направлении. Для отыскания «быстроты» изменения поля служит вектор, который называется градиентом.
Вектор
![]() ,
называемый градиентом поля
,
называемый градиентом поля
![]() ,
широко используют для характеристики
скалярного поля. Этот вектор направлен
по нормали к поверхности уровня в сторону
максимального возрастания
и равен скорости изменения
в этом направлении:
,
широко используют для характеристики
скалярного поля. Этот вектор направлен
по нормали к поверхности уровня в сторону
максимального возрастания
и равен скорости изменения
в этом направлении:
![]()
 .
.
Зная направление нормали к поверхности уровня (то есть направление наибыстрейшего возрастания величины ) можно вычислить производную по всякому другому направлению. Градиент является не только характеристикой быстроты изменения скалярного поля, но и также мерой его неоднородности.
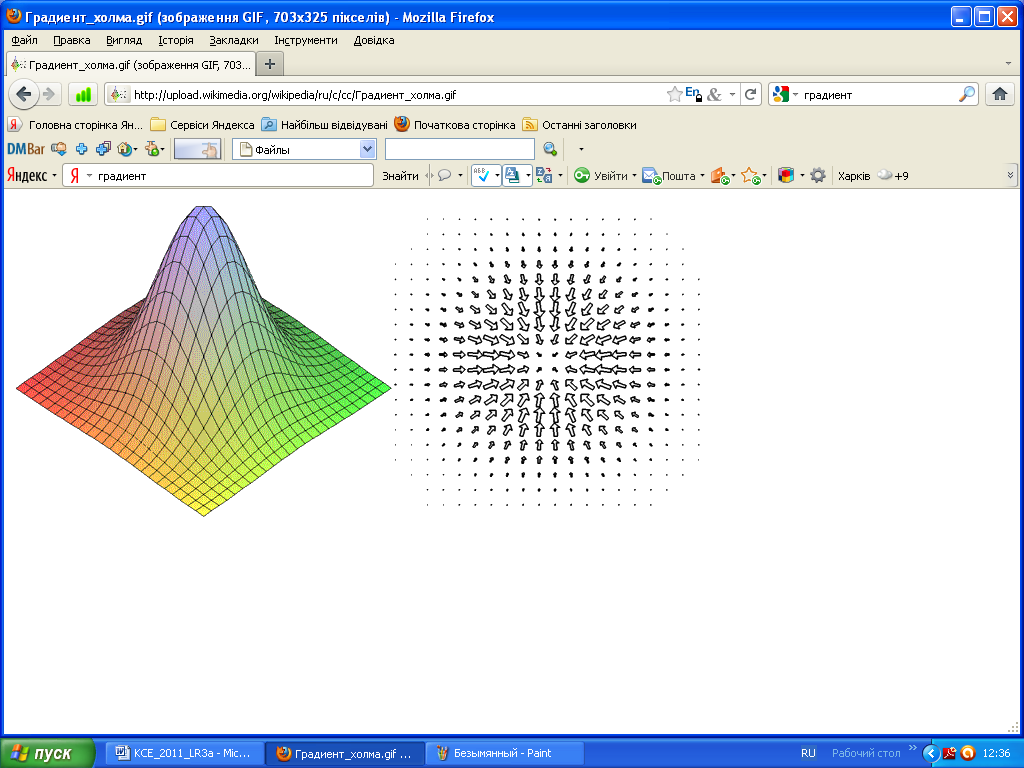
Рис. 3б. Операция градиента преобразует функцию в виде холма (слева) в поле векторов (справа). Видно, что вектора градиента направлены в горку и тем длиннее, чем круче наклон.
Своим появлением на свет понятие
градиента обязано выдающемуся шотландскому
физику, создателю математической теории
электромагнитного поля Джеймсу Клерку
Максвеллу (1831-1879) и происходит от
латинского слова
![]() ,
означающего расти. Главное свойство
градиента состоит в том, что он
определяет направление наибыстрейшего
спуска. Поэтому Максвелл даже собирался
назвать этот вектор словом
,
означающего расти. Главное свойство
градиента состоит в том, что он
определяет направление наибыстрейшего
спуска. Поэтому Максвелл даже собирался
назвать этот вектор словом
![]() - «склон».
- «склон».
Посредством так называемых силовых векторных полей, которые создаются в окружающем пространстве, может осуществляться взаимодействие между материальными объектами, частицами вещества, удаленными друг от друга.
Разновидность материи, посредством которой осуществляется бесконтактное взаимодействие, называется силовым полем. Силовые поля столь же материальны, как и их источники- частицы или тела. Можно говорить, что векторные поля обладают массой (не локализованной, а «размазанной» по пространству), что они перемещаются с какой-то скоростью. Вам известно, что скорость перемещения таких полей огромна – она равна 300 000 км/сек.
Применение для характеристики силовых полей векторов, когда в каждой точке рассматриваемой области пространства ставится в соответствие вектор, позволяет отображать многое физические закономерности в экономной и универсальной форме.
Если в каждой точке
из
определен вектор
![]() ,
то говорят, что в области
задано векторное поле. Функция
,
то говорят, что в области
задано векторное поле. Функция
![]() ,
с помощью которой задается векторное
поле, называется векторной функцией.
,
с помощью которой задается векторное
поле, называется векторной функцией.
Если в области пространства каждая
точка
![]() задана некоторым вектором
задана некоторым вектором
![]() ,
то в данной области определено векторное
поле.
,
то в данной области определено векторное
поле.
Напомним, что в математике вектор
,
заданный в трехмерном пространстве с
декартовыми координатами![]() может быть представлено тремя проекциями
на выбранные оси:
может быть представлено тремя проекциями
на выбранные оси:
![]() ,
,
где
![]() -
единичные векторы (орты) вдоль указанных
осей x, y, z
-
единичные векторы (орты) вдоль указанных
осей x, y, z
![]() - проекции вектора оси x,
y, z.
- проекции вектора оси x,
y, z.
Наглядно представить в графическом виде векторное поле весьма не просто. Для этого используют различные «ухищрения». В частности, графически силовые векторные поля удобно изображать с помощью картин силовых линий – пространственных кривых, обладающих тем свойством, что в каждой их точке вектор поля направлен вдоль касательной.
С помощью силовых линий наглядно изображается электрическое поле.
Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м2, перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля.
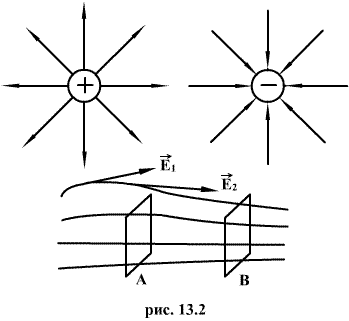
Рис. 3в. Картина силовых линий электрического поля. Величине напряженности поля через площадку В больше, так как через нее проходит 4 линии
Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным.
В настоящее время научно доказано существование двух силовых полей – гравитационного и электромагнитного. Силы, создаваемые этими полями (из-за чего их и называют силовыми), действуют на расстоянии между покоящимися и движущимися частицами или телами.
Заметим, что начиная с 1905 года, благодаря Альберту Эйнштейну, ученые стали пересматривать свои взгляды на мир и постепенно отказываться от механистических взглядов на Вселенную, начало которым положил Ньютон своими законами механики. Они стали объяснять происходящее понятиями полей. Этот новый взгляд на Вселенную с точки зрения теории поля помог ученым продвинуться вперед там, где это было невозможно во времена, когда господствовал механистический подход. Все что считалось силой толчок-тяга, ныне рассматривается как взаимодействие полей. В частности, воздействия типа «тяни – толкай», в первом, весьма грубом приближении, с точки зрения взаимодействия полей можно изложить следующим образом. Вам известно, что атомы состоят из электронов. Когда два атома приближаются друг к другу, окружающие электроны электромагнитные поля взаимно отталкиваются. Сами атомы расходятся, по существу не касаясь друг друга. Поэтому, когда мы толкаем прут или его тянем, то в действительности не соприкасаемся с чем либо твердым. Мы используем эти крошечные электромагнитные поля.
Всю совокупность электромагнитных явлений принято разделять на две группы: электрические и магнитные явления. Взаимодействие заряженных частиц и тел осуществляется через материального посредника, называемого электрическим полем. К подробному изучению свойств стационарного электрического поля мы и приступим.
Эксперимент 1. Изучение посредством моделирования основных понятий, связанных со стационарным электрическим полем.
Электрические свойства тел определяются
их зарядами. Понятие электрического
заряда Вам знакомо из школы. В курсе
физики вам рассказывали о фактах, на
основании которого формируется понятие
электрического заряда. Заряд, как
физическая величина обозначается
![]() и измеряется в кулонах [Кл]. Элементам
микромира присущи, как положительные,
так и отрицательные заряды. Строение
вещества обычно таково, что заряды
уравновешены. Наименьший по абсолютной
величине отрицательный заряд
и измеряется в кулонах [Кл]. Элементам
микромира присущи, как положительные,
так и отрицательные заряды. Строение
вещества обычно таково, что заряды
уравновешены. Наименьший по абсолютной
величине отрицательный заряд
![]() =1,6021892х10-19
Кл, ассоциируется с представлением об
элементарной частице, именуемой
электроном.
=1,6021892х10-19
Кл, ассоциируется с представлением об
элементарной частице, именуемой
электроном.
Вам уже известно, что вокруг заряда существует электрическое поле. Оно окружает заряд даже в вакууме. Если заряд покоится (неподвижен) то говорят, что вокруг него электростатическое электрическое поле. Такое поле еще называют связанным, потому что оно неразрывно связано с электрическим зарядом. Вам демонстрировали, что если к заряженному телу, то есть к телу, содержащему заряды одного знака, поднести так называемый пробный (точечный, очень малой величины, чтобы он не искажал поле) заряд, то на пробный заряд начнет действовать сила, свидетельствующая о том, что в пространстве вокруг заряженного тела существует электрическое поле. Взаимодействие пробного заряда и электрического поля происходит бесконтактно, поэтому сила действует на заряд на расстоянии.
В школе Вам говорили, что сила
взаимодействия двух точечных зарядов
![]() и
и
![]() (простейший случай, когда один заряд
создает электростатическое поле, а
второй рассматривается как пробный)
всегда направлена по линии их соединяющей.
Величина этой силы пропорциональна
произведению зарядов и обратно
пропорциональна квадрату расстояния
(простейший случай, когда один заряд
создает электростатическое поле, а
второй рассматривается как пробный)
всегда направлена по линии их соединяющей.
Величина этой силы пропорциональна
произведению зарядов и обратно
пропорциональна квадрату расстояния
![]() между ними. Это так называемый закон
Кулона:
между ними. Это так называемый закон
Кулона:
![]() .
.
Коэффициент пропорциональности
![]() зависит от того, в какой системе единиц
Вы работаете.
зависит от того, в какой системе единиц
Вы работаете.
Для справедливости приведенной формулы требуется, чтобы среда, в которой находятся взаимодействующие точечные заряды, была однородной изотропной и безграничной.
Однородность среды означает, что ее свойства одинаковы во всех ее точках (в частности, одинаков состав и нет никаких вкраплений).
Изотропность означает, что свойства этой среды в окрестности каждой ее точки одинаковы во всех направлениях.
Понятие безграничности на практике означает, что размеры изучаемого образца, в котором находятся заряды, во много раз превышает расстояние между ними.
Сила взаимодействия заряда с полем
зависит от величины этого заряда. Если
брать различные пробные заряды, то сила
![]() ,
действующая на них в данной точке
электрического поля, будет различной.
Отношение силы, действующей на заряд,
к величине этого заряда называется
напряженностью электрического поля.
,
действующая на них в данной точке
электрического поля, будет различной.
Отношение силы, действующей на заряд,
к величине этого заряда называется
напряженностью электрического поля.
Напряженность поля есть вектор,
поэтому она характеризует поле в каждой
его пространственной точке по величине
и по направлению. Математическая модель
электрического поля в вакууме -
![]() .
Если пространство характеризуют
радиус-вектором
,
то напряженность электрического поля
записывают в виде
.
Если пространство характеризуют
радиус-вектором
,
то напряженность электрического поля
записывают в виде
![]() .
Формула напряженности электрического
поля:
.
Формула напряженности электрического
поля:
 .
.
Из формулы следует, что напряженность
есть действующая на единичный положительный
заряд сила
![]() ,
возникающая в результате бесконтактного
взаимодействия между электрическим
полем и зарядом.
,
возникающая в результате бесконтактного
взаимодействия между электрическим
полем и зарядом.
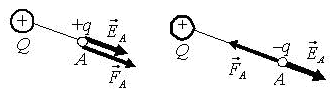
Рис. 3г. Направление вектора напряженности
электрического поля при взаимодействии
двух точечных зарядов
![]() и
(простейший случай, когда заряд Q
создает электростатическое поле, а
второй q
рассматривается как пробный)
и
(простейший случай, когда заряд Q
создает электростатическое поле, а
второй q
рассматривается как пробный)
Часто приходится рассматривать
электрические процессы в атмосфере,
которая по своим свойствам весьма
незначительно отличается от вакуума.
В этом случае для описания электрического
поля достаточно использовать лишь
вектор
![]() ,
который для краткости часто называют
электрическим вектором.
,
который для краткости часто называют
электрическим вектором.
Если требуется описывать электрическое
поле в материальной среде, например,
внутри диэлектрика, то обычно
используют понятие векторного поля
![]() ,
называемое полем электрического
смещения (или электрической индукции).
Вектор
в вакууме связан с вектором
соотношением
,
называемое полем электрического
смещения (или электрической индукции).
Вектор
в вакууме связан с вектором
соотношением
![]() ,
,
где
![]() -
фундаментальная физическая константа,
называемая электрической постоянной.
Значение электрической постоянной
найдено экспериментально; с точностью
вполне достаточной для расчетов
-
фундаментальная физическая константа,
называемая электрической постоянной.
Значение электрической постоянной
найдено экспериментально; с точностью
вполне достаточной для расчетов
![]() =8.842х10-12
Ф/м;
=8.842х10-12
Ф/м;
![]() -диэлектрическая
постоянная среды.
-диэлектрическая
постоянная среды.
Надо иметь в виду, что кроме силового действия поля на заряд, по которому обычно судят о его характеристиках, электростатическое поле обладает и рядом других свойств. В частности можно говорить, что оно обладает определенным запасом энергии, имеет массу. Все процессы, происходящие с участием электрического поля, подчиняются следующим законам: закону сохранения энергии, закону сохранения импульса, закону сохранения момента импульса. Это дает основание говорить о сходстве (внутреннем единстве) вещественных объектов и полей, о присущности этим двум видам материи таких общих черт:
а) вещество и поле обладают энергией;
б) все процессы, происходящие в поле, подчиняются основным законам сохранения.
Но электростатическое поле и вещество обладают и рядом существенных свойств, которые позволяют их различать:
а) поля, в отличие от вещества, не имеют определенной пространственной локализации, точно указать их границу невозможно;
б) один и тот же объем пространства не может быть занят одновременно несколькими вещественными объектами (в частности, вам хорошо известно, что на стоянке в одно то же место нельзя поставить несколько машин). В одном и том же объеме могут существовать несколько электростатических полей.
в) материальные частицы или вещественные объекты могут двигаться с любой скоростью, не превышающей скорости света. Для полей существуют только две скорости: нулевая – для статических полей и скорость света для свободных полей (полей, как бы отрывающихся от заряда и распространяющихся в пространстве в виде электромагнитных волн).
Статическое электрическое поле удобно изображать графически с помощью картины так называемых силовых (векторных) линий или линий напряженности.
Линией напряженности электрического поля называется линия (помеченная стрелочкой), касательная к которой в каждой точке пространства (поля) совпадает с направлением напряженности.
Если поле создается маленьким заряженным шариком или точечным зарядом, то линии напряженности представляют собой прямые помеченные стрелочкой, радиально (по направлению радиуса) расходящиеся от заряда или от центра шарика.
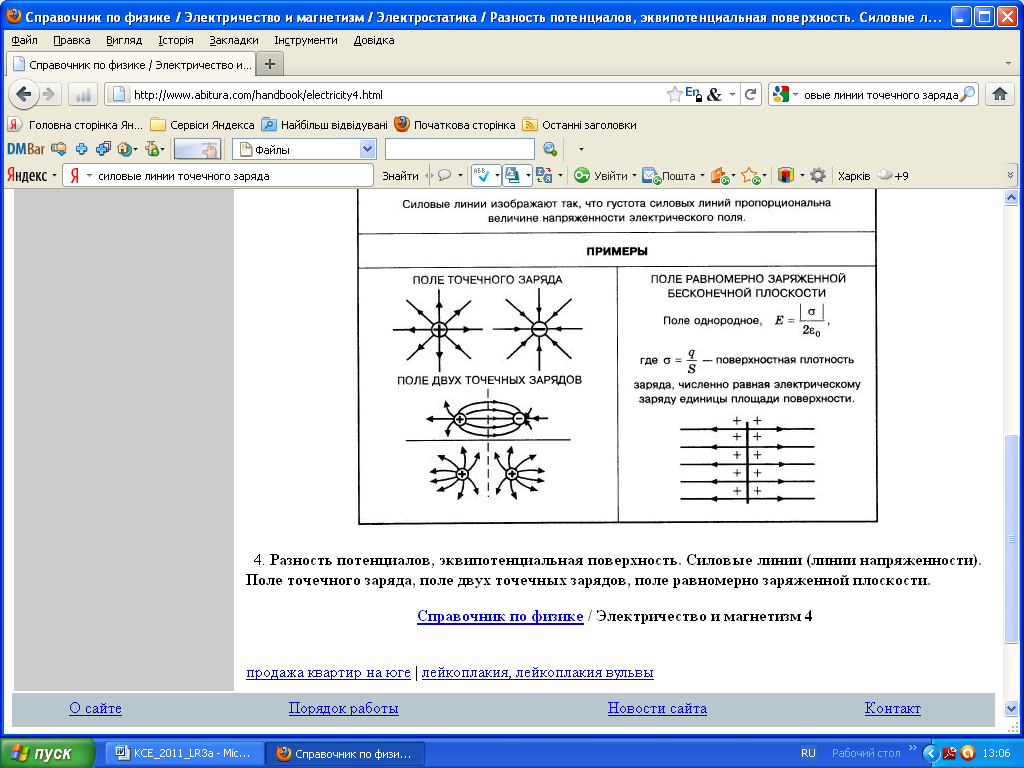
Важно иметь в виду, что силовые линии электростатического поля не должны быть замкнутыми. Действительно, при перемещении заряда вдоль силовой линии силами поля совершается работа, так как сила направлена все время вдоль пути. Если бы силовая линия была замкнутой, то при перемещении заряда вдоль такой линии с возвращением в исходную точку производилась бы работа, тогда как работа, производимая силами консервативного поля на замкнутом пути, равна нулю.
Таким образом, силовые линии электрического поля должны обязательно где-то начинаться или кончаться, либо уходить на бесконечность одним из своих концов.
Точками начала или конца силовой линии являются создающие поле заряды. Что касается бесконечности, то силовая линия не может уходить туда обоими своими концами. В противном случае, при переносе заряда вдоль такой линии из бесконечности в бесконечность производилась бы некоторая работа в противоречии с тем, что на обоих концах пути потенциальная энергия равна нулю. Поэтому одним концом силовой линии должен быть обязательно заряд, другой же ее конец может находиться либо на бесконечности, либо на заряде противоположного знака.
При этом часто более сильное поле изображается более плотно расположенными линиями напряженности. Такой способ удобен и естественен, поскольку в отсутствие поля силовых линий не должно быть совсем. Линия напряженности отрицательного заряда отличается от линии положительного заряда лишь направлением линии (направлением помечающей стрелки).
На рис. 3в изображены силовые линии поля двух зарядов противоположного знака, причем положительный заряд больше отрицательного. Поэтому часть линий исходящих из положительного заряда заканчивается на отрицательном, а часть уходит на бесконечность.
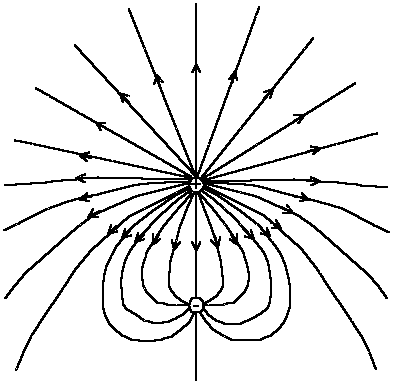
Рис. 3д. Графическое изображение статического электрического поля двух точечных зарядов в виде силовых линий, представляющих линии напряженности электрического поля
Чтобы не возникало недоразумений, сразу же подчеркнем важное обстоятельство: пользуясь картиной линий поля, причем ее плоским изображением, не следует забывать, что линии поля не существуют реально, а являются лишь наглядным средством изображения электрического поля, которое дает лишь качественную картину поля и демонстрирует его структуру. Точное описание электрического поля в пространстве можно получить только с помощью математической теории векторного поля, которая называется векторным анализом.
Если поле создается не одним точечным зарядом, а несколькими, то картина силовых полей будет иметь более сложный вид (рис.4).
Обратите внимание на то обстоятельство, что при компьютерном изображении силовых линий изображение сплошной линии напряженности электрического поля заменяется набором определенной длины стрелок. Длина и направление стрелок в точке, откуда они исходят, зависят от величины напряженности. Поскольку напряженность есть действующая на единичный положительный заряд сила , то стрелки, характеризующие вектор напряженности электрического поля, также представляют совокупность векторов сил, возникающих в результате бесконтактного взаимодействия между электрическим полем и заряженным телом, имеющим положительный заряд. Глядя на картину поля легко представить, как вместо набора стрелок получается сплошная силовая линия напряженности электрического поля, поскольку в каждой точке пространства (поля) вектора напряженности (силы) являются касательными к линии напряженности.

Рис. 4. Графическое изображение статического электрического поля нескольких точечных зарядов с помощью стрелок, представляющих в прерывистом виде силовые линии напряженности электрического поля
На рис.4 имеется несколько выделенных разным цветом характерных типов фрагментов картины силовых линий, которые обычно встречаются при исследовании векторных полей и которые характеризуют структуру поля.
Несложно заметить, что существуют области, в которых линии сил начинаются или оканчиваются (они выделены не светло-зеленым цветом). Кроме того, имеются фрагменты картины, где линии напряженности либо уходят на бесконечность, либо оттуда приходят (участки светло-зеленого цвета). Область картины силовых линий может содержать точку, из которой расходятся силовые линии. Эту точку, в которой линии поля начинаются, называют исток. Точку, в которую сходятся все силовые линии, называют стоком.
К сожалению, рассмотренные способы графического изображения электрического поля дают достаточно полную картину векторного поля только в случае, когда оно плоское, то есть все векторы располагаются в одной плоскости и зависят от двух координат. В общем же случае произвольного пространственного поля приходится дополнять графическое поле неким додуманным пространственным воображением. Охарактеризовать особенности структуры того или иного векторного поля в окрестности заданной точки значительно сложнее, чем в случае скажем скалярного поля, так как векторы могут меняться от точки к точке, не только по абсолютной величине (по длине), но и по направлению.
Кроме того следует иметь в виду, что часто наиболее бросающиеся в глаза отличия оказываются второстепенными, а действительную важность имеют тонкие, но не очевидные особенности структуры. Для того, чтобы глубже уяснить эти особенности, а также понять, что представляют собой истоки и стоки и чем они характеризуются, введем несколько важных понятий.
Всякий вектор можно рассматривать как
сумму трех векторов, параллельных
осям координат. Пусть
![]() ,
и
,
и
![]() - проекции вектора
на оси координат Ох, Оy,
Oz соответственно, то есть
для любой точки М задано векторное поле
- проекции вектора
на оси координат Ох, Оy,
Oz соответственно, то есть
для любой точки М задано векторное поле
![]() ,
,
где
![]() -
единичные орты, с которыми связана
прямоугольная система координат Oxyz
(говорят часто, что система образует
ортонормированный базис).
-
единичные орты, с которыми связана
прямоугольная система координат Oxyz
(говорят часто, что система образует
ортонормированный базис).
Если в некоторой области
![]() ,
ограниченной поверхностью
,
ограниченной поверхностью
![]() векторное поле
векторное поле
![]() таково, что функции
таково, что функции
![]() непрерывны в
вместе с частными производными, то для
такого поля можно ввести понятие
дивергенции.
непрерывны в
вместе с частными производными, то для
такого поля можно ввести понятие
дивергенции.
Дивергенцией векторного поля
называется скалярная функция
![]() ,
определяемая равенством
,
определяемая равенством
 .
.
Роль своеобразного «эталона» структуры поля, когда интересуются не только структурой полей, но и их физической природой, играет обычно поле скоростей несжимаемой жидкости, с которым сравниваются другие поля. Видимо поэтому дивергенцию векторного поля называют еще расходимостью. Она определяет скорость изменения каждой компоненты вектора в своем «собственном» направлении.
Пусть вектор
![]() означает скорость течения несжимаемой
жидкости. Назовем количество жидкости,
вытекающее из замкнутой оболочки
положительным потоком, а втекающий
в нее отрицательным.
означает скорость течения несжимаемой
жидкости. Назовем количество жидкости,
вытекающее из замкнутой оболочки
положительным потоком, а втекающий
в нее отрицательным.
Если векторное поле описывает поток
несжимаемой жидкости, то положительность
дивергенции (![]() )
в данной точке означает, что из такой
точки вытекает больше жидкости, чем в
нее притекает. Говорят, что такая точка
служит источником. Если же
)
в данной точке означает, что из такой
точки вытекает больше жидкости, чем в
нее притекает. Говорят, что такая точка
служит источником. Если же
![]() ,
то наблюдается обратный баланс и точка
служит стоком, то есть в нее притекает
больше, чем вытекает. Если же
,
то наблюдается обратный баланс и точка
служит стоком, то есть в нее притекает
больше, чем вытекает. Если же
![]() ,
то существует баланс – жидкости притекает
столько же, сколько и вытекает. Если
,
то поле бездивергентно, то есть в случае
несжимаемой жидкости полный поток из
любой замкнутой оболочки (говорят также
«через любую замкнутую оболочку») должен
быть равен нулю.
,
то существует баланс – жидкости притекает
столько же, сколько и вытекает. Если
,
то поле бездивергентно, то есть в случае
несжимаемой жидкости полный поток из
любой замкнутой оболочки (говорят также
«через любую замкнутую оболочку») должен
быть равен нулю.
Для изучаемого случая статического электрического поля системы зарядов дивергенция характеризует расходимость или сходимость векторов поля.
Рассмотрим внимательно картину силовых линий электростатического поля (рис. 3).
Для областей, имеющих сине-фиолетовый оттенок, вектора выходят. Следовательно, в данной области имеет место источник и для подобных областей имеет место расходимость векторов, дивергенция положительна .
Для областей, имеющих красно-желтый оттенок, вектора входят («втекают»). Следовательно, для подобных областей имеет место сходимость векторов, дивергенция отрицательна и в данной области имеет место сток.
Источники характеризуются своей величиной или своей так называемой мощностью.
Мысленно представьте, что источник вы окружили некоторой поверхностью (пока не важно, что в плоском представлении она на рис. 1 является в виде прямоугольника). Эту поверхность пересекают несколько силовых линий (подобно жидкости, которая вытекает), которые характеризуются потоком вектора через поверхность.
Потоком через поверхность называется число линий вектора, пересекающих эту поверхность. Мощность источника определяется потоком через замкнутую поверхность окружающую этот источник.
Чтобы стало более понятно, о чем идет
речь, рассмотрим поток напряженности
электрического поля, создаваемого
точечным зарядом, через сферу, в центре
которой он находится. Напряженность
электрического поля на поверхности
сферы радиуса
равна
![]() .
С другой стороны, напряженность равна
количеству линий, проходящих через 1
см2, поэтому поток
.
С другой стороны, напряженность равна
количеству линий, проходящих через 1
см2, поэтому поток
![]() через сферу поверхность которой
через сферу поверхность которой
![]() равен
равен
![]() .
.
Ясно, что если вместо сферы взять другую замкнутую поверхность, то поток останется тем же самым, так как все линии, проходящие через эту сферу, проходят и через эту поверхность.
Итак, электростатическое поле могут создавать физические объекты двух совершенно разных видов: источники и стоки. У источников поток вектора напряженности положителен, поскольку его силовые линии выходят из поверхности наружу. У стоков поток отрицательный, так как линии входят внутрь. При этом, чем больше густота линий, тем больше поток и больше интенсивность поля.
Теорема Остроградского –Гаусса утверждает, что полный поток напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов , находящихся внутри этой поверхности :
![]() .
.
Когда мы рассматривали понятие механической работы, то мы установили, что если поднять груз на некоторую высоту (работа отрицательна), а затем опустить его на прежний уровень (работа та же, но положительная), то полная механическая работа, совершаемая силой тяжести (которая действует благодаря гравитационному полю) будет равна нулю. Тогда же мы ввели очень важное свойство потенциальности.
Установлено, что, кроме гравитационного поля, свойством потенциальности обладает и электростатическое поле, образованное несколькими неподвижными зарядами.
Электрическое поле называется потенциальным, если работа, которую совершает поле над зарядом, при перемещении его по любому замкнутому пути равняется нулю. Кроме этого определения, часто используют и другое эквивалентное определение.
Электрическое поле называется потенциальным, если работа по перемещению заряда между любыми точками 1 и 2 не зависит от формы пути, а зависит только от положения начальной и конечной точек пути.
Для потенциального поля вводят и широко используют понятие электрического потенциала.
Электрическим потенциалом
![]() данной точки поля называется работа,
которую нужно затратить, чтобы переместить
положительный единичный заряд из
бесконечности в данную точку поля. О
потенциале можно сказать и по-другому:
это работа
данной точки поля называется работа,
которую нужно затратить, чтобы переместить
положительный единичный заряд из
бесконечности в данную точку поля. О
потенциале можно сказать и по-другому:
это работа
![]() ,
которую затрачивает поле, перемещая
единичный положительный заряд из данной
точки поля в бесконечность.
,
которую затрачивает поле, перемещая
единичный положительный заряд из данной
точки поля в бесконечность.
Заметим, что указанная работа положительна, если заряд перемещаем против сил поля, и отрицательна в противоположном случае.
Под «бесконечностью» понимается область пространства, столь далекая от всех электрических зарядов, что в этой области поле можно считать равным нулю.
При данной точке зрения на определение
потенциала бесконечность это некая
абстрактная точка отсчета, в которой
потенциал равен нулю
![]() .
Однако такой подход, используемый в
физике, не является обязательным. В ряде
технических наук, в частности в
электротехнике и электронике, нулевым
потенциалом считают потенциал Земли.
.
Однако такой подход, используемый в
физике, не является обязательным. В ряде
технических наук, в частности в
электротехнике и электронике, нулевым
потенциалом считают потенциал Земли.
Любая система неподвижных зарядов создает потенциальное электростатическое поле, которое можно характеризовать электрическим потенциалом.
Можно показать, что для одного точечного заряда потенциал равен
![]() .
.
Следовательно, точечный заряд на расстоянии создает потенциал . При этом потенциал может быть положительным или отрицательным, в зависимости от знака заряда, который его создает.
Если быть точным, то следует отметить, что потенциал, это некоторая характеристика состояния - способности (возможности) поля совершать работу. Заряд создает вокруг себя электрическое поле, которое обладает способностью совершить работу. То есть, как мы отмечали ранее это энергия. Эту энергию заряда и характеризует потенциал. Энергия заряда зависит от величины заряда и от точки пространства (расстояния) в которой мы оцениваем эту способность. Только если в данную точку поместить единичный пробный заряд, то на этот заряд начнет действовать сила, которая начнет перемещать заряд и способность (возможность) совершить работу перейдет в действительность, то есть в процесс совершения работы. Без пробного заряда полю не над чем совершать работу. Если нет пробного заряда, то потенциал характеризует состояние (энергию), как говорят, потенциальную возможность поля совершить работу.
Следует иметь в виду, что напряженность
электрического поля – величина векторная,
а потенциал – скалярная. В каждой точке
поля потенциал
имеет одно определенное численное
значение. Напряженность же задается в
каждой точке тремя величинами – тремя
проекциями на оси координат
![]() .
.
В этой связи удобно поле, создаваемое заряженным телом (зарядом) или несколькими телами наглядно представлять в виде потенциальной диаграммы – графика зависимости потенциала (или потенциальной энергии) от координат.
Точки, в которых потенциал имеет заданное
фиксированное значение, располагаются
на поверхностях, называемых
эквипотенциальными поверхностями.
Из формулы
![]() следует, что эквипотенциальные поверхности
поля точечного заряда представляют
собой систему сфер с радиусом
следует, что эквипотенциальные поверхности
поля точечного заряда представляют
собой систему сфер с радиусом
![]() или
на плоскости – систему кругов разных
радиусов.
или
на плоскости – систему кругов разных
радиусов.
Введение понятия потенциала чрезвычайно упрощает решение электростатических задач. Оказалось, что зная потенциал, можно относительно просто найти напряженность электрического поля. Вы вправе спросить, а верно ли утверждение о том, что по одной величине можно определить три. Нельзя, конечно, если они не связаны. Но дело все в том, что величины связаны между собой. Эта связь обусловлена условиями потенциальности, согласно которому работа поля на замкнутом пути равна нулю.
Для определения потенциала любой системы
заряженных тел можно записать и
относительно просто решить уравнения
(Пуассона, Лапласа). Если потенциал вдоль
одной координаты известен, например,
вдоль х, то величина
![]() ,
имеющая смысл падения потенциала,
приходящегося на единицу длины координаты
х, и будет напряженностью. Несложно
догадаться, что напряженность и сила,
действующая на пробный заряд больше
там, где график потенциала (потенциальная
диаграмма) изменяется быстрее. Там
где график не меняется вдоль координаты,
напряженность равна нулю.
,
имеющая смысл падения потенциала,
приходящегося на единицу длины координаты
х, и будет напряженностью. Несложно
догадаться, что напряженность и сила,
действующая на пробный заряд больше
там, где график потенциала (потенциальная
диаграмма) изменяется быстрее. Там
где график не меняется вдоль координаты,
напряженность равна нулю.
Градиентом скалярной величины называется вектор, имеющий направление наиболее быстрого возрастания этой величины, а по модулю равный ее изменению на единицу длины. Формулу читают так: напряженность есть минус градиент потенциала.
Изменение потенциала при переходе от одной эквипотенциальной поверхности к другой наиболее быстро меняется в направлении, соединяющем эти поверхности. То есть самым коротким из всех направлений является тот путь, который нормален (перпендикулярен) к эквипотенциальной поверхности. Следовательно, наиболее быстро потенциал меняется вдоль линии, которая определяет напряженность. Для эквипотенциальных поверхностей электрического поля точечного заряда, которые представляют сферы (круги), потенциал быстрее всего меняется вдоль прямых исходящих из центра сферы (круга). Поэтому линии напряженности электрического поля – исходящие из центра лучи.
Известное из механики понятие потенциальной энергии относится и потенциальному электростатическому полю.
Потенциальной энергией тела
![]() называют ту работу, которую нужно
затратить, чтобы переместить это тело
из бесконечности в данную точку. При
этом работа не зависит от формы пути.
называют ту работу, которую нужно
затратить, чтобы переместить это тело
из бесконечности в данную точку. При
этом работа не зависит от формы пути.
Потенциальная энергия заряда простым образом связана с потенциалом той точки поля, где заряд находится. Поскольку потенциал есть работа перенесения единичного заряда, то потенциальная энергия равна произведению заряда на потенциал . То есть, потенциальная энергия заряда в электростатическом потенциальном поле равна
![]() .
.
Обладают потенциальной энергией и взаимодействующие между собой электрические заряды. Потенциальная энергия взаимодействия двух точечных зарядов, находящихся на расстоянии в пустоте, равна
 .
.
При бесконечно большом расстоянии между
зарядами
![]() .
.
Если заряды отталкиваются, то есть имеют одинаковый знак, то потенциальная энергия зарядов положительна. Если заряды притягиваются, то есть имеют разные знаки, то потенциальная энергия их взаимодействия отрицательна.
Обратите внимание на то, что силы электрического поля всегда направлены в сторону уменьшения потенциальной энергии. Отталкивающиеся одноименные заряды стремятся увеличить взаимное расстояние, то есть уменьшить их положительную энергию. Притягивающиеся разноименные заряды стремятся сблизится, а сближение приводит снова-таки к уменьшению потенциальной энергии.
Отметим, что выделение потенциальных полей в отдельный класс очень важно.
Если силовое поле имеет однозначный потенциал, то вычисление работы сил поля сводится к определению разности потенциалов в начальной и конечной точках пути. Это намного упрощает многие расчеты статического электрического поля.
Введите в командное окно MATLAB програму 1.
Изучите, какой вид будут иметь картина силовых линий в случае, когда электрическое поле создается несколькими зарядами.
Програма 1.
x = -3:.2:3;
y = -3:.2:3;
[xx,yy] = meshgrid(x,y);
zz = peaks(xx,yy);
hold on
pcolor(x,y,zz);
axis([-3 3 -3 3]);
colormap((jet+white)/2);
shading interp
[px,py] = gradient(zz,.2,.2);
quiver(x,y,px,py,2,'k');
axis off
hold off
Введите в командное окно MATLAB програму 2.
Изучите, какой вид будут иметь потенциальная диаграмма (фигура 1), семейство эквипотенциальных линий (фигура 2) и картина линий напряженности поля (фигура 3), в случае, когда электростатическое поле создается одним положительным зарядом.
Програма 2.
clear;
e=1.6*10^-16;
R0=10^-8;
N=1;
i=1:N;
q(1)=e;
x1=-0.1*R0;
x2=5*R0;
xq(i)=x1+(x2-x1)*i/N;
yq(i)=0;
N1=23;
Xmin=-4*R0;
Ymin=-6*R0;
Xmax=8*R0;
Ymax=10*R0;
i=1:N1+1;
X(i)=Xmin+(Xmax-Xmin)/N1*(i+1);
j=1:N1+1;
Y(j)=Ymin+(Ymax-Ymin)/N1*(j+1);
e0=8.85*10^-12;
Nq=length(q);
Nx=length(X);
Ny=length(Y);
for i=1:Ny
for j=1:Nx
s=0;
for k=1:Nq
s=s+q(k)./((X(j)-xq(k)).^2+(Y(i)-yq(k)).^2).^0.5;
end;
M(i,j)=s./(4*pi*e0);
end;
end;
[X1,Y1]=meshgrid(X,Y);
[px,py]=gradient(-M,0.1,0.1);
px1=px./(px.^2+py.^2).^0.5;
py1=py./(px.^2+py.^2).^0.5;
surf(X1,Y1,M);
figure(2);
[C,h]=contour(X1,Y1,M);
clabel(C,h)
colormap cool
figure(3);
quiver(X1,Y1,px1,py1,0.6)
Кратко опишите, какие типичные фрагменты структуры электрического поля имеются в картине силовых линий точечного положительного заряда (является ли везде поле однородным)?
Сформулируйте, что представляют собой линии напряженности электрического поля?
На основании картины линий напряженности электрического поля и знака у потока силовых линий, сделайте заключение о том, является точечный положительный заряд источником или стоком.
Представьте, что в полученное графически электростатическое поле в какую-то его точку попадает пылинка (или молекула газа), имеющая положительный заряд. Объясните, что будет происходить с пылинкой имеющей положительный заряд в электростатическом поле.
Представьте, что в какую-то точку исследуемого электростатического поля попадает пылинка (или молекула газа), имеющая отрицательный заряд. Объясните, что будет происходить с пылинкой имеющей отрицательный заряд в электростатическом поле.
Сделайте вывод о том, что происходит с потенциалом по мере увеличения расстояния от точки нахождения заряда; выполняется ли условие, что потенциал точечного заряда на бесконечности стремиться к нулю.
Какую форму на плоскости представляет семейство эквипотенциальных линий? (Имейте при этом в виду, что из-за погрешностей расчетов отдельные кривые в точке расположения заряда состоят из прямоугольных отрезков и лишь по мере отдаления от него приближаются к системе кругов разных радиусов).
Анализируя потенциальную диаграмму (фигура 1) и семейство эквипотенциальных линий, определите, в каком направлении наиболее быстро меняется потенциал.
Рассмотрите снова случаи, когда сначала положительная, а затем отрицательно заряженная пылинка (или молекула газа), попадает в какую-то точку электростатического поля. Объясните, что будет происходить с пылинками с точки зрения того, как меняться потенциал и потенциальная энергия при их перемещении. Проведите аналогию с упругим мячиком, оказавшимся на склоне горы. Сделайте заключение о том, какой вид движения будет у пылинок (равномерный, равноускоренный, равнозамедленный).
Введите в командное окно MATLAB програму 3.
Изучите, какой вид будут иметь потенциальная диаграмма (фигура 1), семейство эквипотенциальных линий (фигура 2) и картина линий напряженности поля (фигура 3), в случае, когда электростатическое поле создается одним отрицательным зарядом.
Програма 3.
clear;
e=1.6*10^-16;
R0=10^-8;
N=1;
i=1:N;
q(1)=-e;
x1=-0.1*R0;
x2=5*R0;
xq(i)=x1+(x2-x1)*i/N;
yq(i)=0;
N1=23;
Xmin=-4*R0;
Ymin=-6*R0;
Xmax=8*R0;
Ymax=10*R0;
i=1:N1+1;
X(i)=Xmin+(Xmax-Xmin)/N1*(i+1);
j=1:N1+1;
Y(j)=Ymin+(Ymax-Ymin)/N1*(j+1);
e0=8.85*10^-12;
Nq=length(q);
Nx=length(X);
Ny=length(Y);
for i=1:Ny
for j=1:Nx
s=0;
for k=1:Nq
s=s+q(k)./((X(j)-xq(k)).^2+(Y(i)-yq(k)).^2).^0.5;
end;
M(i,j)=s./(4*pi*e0);
end;
end;
[X1,Y1]=meshgrid(X,Y);
[px,py]=gradient(-M,0.1,0.1);
px1=px./(px.^2+py.^2).^0.5;
py1=py./(px.^2+py.^2).^0.5;
surf(X1,Y1,M);
figure(2);
[C,h]=contour(X1,Y1,M);
clabel(C,h)
colormap cool
figure(3);
quiver(X1,Y1,px1,py1,0.6)
Кратко опишите, какие типичные фрагменты структуры электрического поля имеются в картине силовых линий точечного отрицательного заряда (является ли везде поле однородным)?
Сформулируйте, что представляют собой линии напряженности электрического поля?
На основании картины линий напряженности электрического поля и знака у потока силовых линий, сделайте заключение о том, является точечный отрицательный заряд источником или стоком.
Представьте, что в полученное графически электростатическое поле в какую-то его точку попадает пылинка (или молекула газа), имеющая положительный заряд. Объясните, что будет происходить с пылинкой имеющей положительный заряд в электростатическом поле.
Представьте, что в какую-то точку исследуемого электростатического поля попадает пылинка (или молекула газа), имеющая отрицательный заряд. Объясните, что будет происходить с пылинкой имеющей отрицательный заряд в электростатическом поле.
Сделайте вывод о том, что происходит с потенциалом по мере увеличения расстояния от точки нахождения заряда; выполняется ли условие, что потенциал точечного заряда на бесконечности стремиться к нулю.
Какую форму на плоскости представляет семейство эквипотенциальных линий? (Имейте при этом в виду, что из-за погрешностей расчетов отдельные кривые в точке расположения заряда состоят из прямоугольных отрезков и лишь по мере отдаления от него приближаются к системе кругов разных радиусов).
Анализируя потенциальную диаграмму (фигура 1) и семейство эквипотенциальных линий, определите, в каком направлении наиболее быстро меняется потенциал.
Рассмотрите снова случаи, когда сначала положительная, а затем отрицательно заряженная пылинка (или молекула газа), попадает в какую-то точку электростатического поля. Объясните, что будет происходить с пылинками с точки зрения того, как меняться потенциал и потенциальная энергия при их перемещении. Проведите аналогию с упругим мячиком, попавшим в яму. Сделайте заключение о том, какой вид движения будет у пылинок (равномерный, равноускоренный, равнозамедленный).
Введите в командное окно MATLAB програму 4.
Изучите, какой вид будут иметь потенциальная диаграмма (фигура 1), семейство эквипотенциальных линий (фигура 2) и картина линий напряженности поля (фигура 3), в случае, когда электростатическое поле создается двумя отрицательными и одним положительным зарядами.
Програма 4.
clear;
e=1.6*10^-16;
R0=10^-8;
N=3;
i=1:N;
q(1)=-e;
q(2)=e;
q(3)=-e;
x1=-5*R0;
x2=5*R0;
xq(i)=x1+(x2-x1)*i/N;
yq(i)=0;
N1=23;
Xmin=-9*R0;
Ymin=-9*R0;
Xmax=9*R0;
Ymax=9*R0;
i=1:N1+1;
X(i)=Xmin+(Xmax-Xmin)/N1*(i+1);
j=1:N1+1;
Y(j)=Ymin+(Ymax-Ymin)/N1*(j+1);
e0=8.85*10^-12;
Nq=length(q);
Nx=length(X);
Ny=length(Y);
for i=1:Ny
for j=1:Nx
s=0;
for k=1:Nq
s=s+q(k)./((X(j)-xq(k)).^2+(Y(i)-yq(k)).^2).^0.5;
end;
M(i,j)=s./(4*pi*e0);
end;
end;
[X1,Y1]=meshgrid(X,Y);
[px,py]=gradient(-M,0.1,0.1);
px1=px./(px.^2+py.^2).^0.5;
py1=py./(px.^2+py.^2).^0.5;
surf(X1,Y1,M);
figure(2);
[C,h]=contour(X1,Y1,M);
clabel(C,h)
colormap cool
figure(3);
quiver(X1,Y1,px1,py1,0.4)
Кратко опишите, какие типичные фрагменты структуры электрического поля имеются в картине силовых линий изучаемой системы зарядов (является ли везде поле однородным)?
На основании картины линий напряженности электрического поля и знака у потока силовых линий, сделайте заключение о том, какие заряды являются источниками, а какие стоками.
Картина стрелок, характеризующих электростатическое поле, и указывающих направления действия сил, свидетельствует о том, что положительно заряженная пылинка в зависимости от того, в какую точку пространства она попадет, будет вести себя по-разному. В зависимости от «ландшафта картины» у такой пылинки может быть различные варианты траекторий.
Есть две точки на картине силовых линий, где размещены отрицательные заряды, в которые пылинка будет обязательно притянута (перемещена) окажись она вблизи этих точек. Подобные точки пространства, которые что-то притягивают (в нашем случае пылинку), в настоящее время называют аттракторами (от англ. –to attract - притягивать). Из картины силовых линий видно, что каждый из аттракторов окружен некой четко очерченной областью притяжения. Такая область называется бассейном аттракции (basin, domains of attraction). Граница, отделяющая один бассейн притяжения от другого, называется сепаратриссой (separatrix). То есть, используя новые термины, можно говорить, что в картине изучаемого электростатического поля есть два места, где размещены аттракторы со своими бассейнами.
Представьте, что в полученное графически электростатическое поле в какую-то его точку попадает пылинка (или молекула газа), имеющая положительный заряд. Отметьте на картине силовых линий два аттрактора, их бассейны и сепаратриссы. Объясните, что будет происходить с пылинкой имеющей положительный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Представьте, что в какую-то точку исследуемого электростатического поля попадает пылинка (или молекула газа), имеющая отрицательный заряд. Объясните, что будет происходить с пылинкой имеющей отрицательный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Сделайте вывод о том, какой вид имеет потенциальная диаграмма изучаемой системы зарядов; выполняется ли условие, что потенциал системы зарядов на бесконечности стремиться к нулю.
Какую форму на плоскости представляет семейство эквипотенциальных линий? (Имейте при этом в виду, что из-за погрешностей расчетов отдельные кривые в точке расположения заряда состоят из прямоугольных отрезков и лишь по мере отдаления от него приближаются к системе кругов разных радиусов).
Анализируя потенциальную диаграмму (фигура 1) и семейство эквипотенциальных линий, определите, в каком направлении наиболее быстро меняется потенциал.
Рассмотрите снова случаи, когда сначала положительная, а затем отрицательно заряженная пылинка (или молекула газа), попадает в какую-то точку электростатического поля. Объясните, что будет происходить с пылинками с точки зрения того, как меняться потенциал и потенциальная энергия при их перемещении. Проведите аналогию с упругим мячиком, попавшим в яму. Сделайте заключение о том, какой вид движения будет у пылинок (равномерный, равноускоренный, равнозамедленный).
Введите в командное окно MATLAB програму 5.
Изучите, какой вид будут иметь потенциальная диаграмма (фигура 1), семейство эквипотенциальных линий (фигура 2) и картина линий напряженности поля (фигура 3), в случае, когда электростатическое поле создается двумя положительными и одним отрицательным зарядами.
Програма 5.
clear;
e=1.6*10^-16;
R0=10^-8;
N=3;
i=1:N;
q(1)=e;
q(2)=-e;
q(3)=e;
x1=-5*R0;
x2=5*R0;
xq(i)=x1+(x2-x1)*i/N;
yq(i)=0;
N1=23;
Xmin=-9*R0;
Ymin=-9*R0;
Xmax=9*R0;
Ymax=9*R0;
i=1:N1+1;
X(i)=Xmin+(Xmax-Xmin)/N1*(i+1);
j=1:N1+1;
Y(j)=Ymin+(Ymax-Ymin)/N1*(j+1);
e0=8.85*10^-12;
Nq=length(q);
Nx=length(X);
Ny=length(Y);
for i=1:Ny
for j=1:Nx
s=0;
for k=1:Nq
s=s+q(k)./((X(j)-xq(k)).^2+(Y(i)-yq(k)).^2).^0.5;
end;
M(i,j)=s./(4*pi*e0);
end;
end;
[X1,Y1]=meshgrid(X,Y);
[px,py]=gradient(-M,0.1,0.1);
px1=px./(px.^2+py.^2).^0.5;
py1=py./(px.^2+py.^2).^0.5;
surf(X1,Y1,M);
figure(2);
[C,h]=contour(X1,Y1,M);
clabel(C,h)
colormap cool
figure(3);
quiver(X1,Y1,px1,py1,0.4)
Кратко опишите, какие типичные фрагменты структуры электрического поля имеются в картине силовых линий изучаемой системы зарядов (является ли везде поле однородным)?
На основании картины линий напряженности электрического поля и знака у потока силовых линий, сделайте заключение о том, какие заряды являются источниками, а какие стоками.
Представьте, что в полученное графически электростатическое поле в какую-то его точку попадает пылинка (или молекула газа), имеющая положительный заряд. Отметьте на картине силовых линий аттрактор, его бассейн и сепаратриссу. Объясните, что будет происходить с пылинкой имеющей положительный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Представьте, что в какую-то точку исследуемого электростатического поля попадает пылинка (или молекула газа), имеющая отрицательный заряд. Объясните, что будет происходить с пылинкой имеющей отрицательный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Сделайте вывод о том, какой вид имеет потенциальная диаграмма изучаемой системы зарядов; выполняется ли условие, что потенциал системы зарядов на бесконечности стремиться к нулю.
Какую форму на плоскости представляет семейство эквипотенциальных линий? (Имейте при этом в виду, что из-за погрешностей расчетов отдельные кривые в точке расположения заряда состоят из прямоугольных отрезков и лишь по мере отдаления от него приближаются к системе кругов разных радиусов).
Анализируя потенциальную диаграмму (фигура 1) и семейство эквипотенциальных линий, определите, в каком направлении наиболее быстро меняется потенциал.
Рассмотрите снова случаи, когда сначала положительная, а затем отрицательно заряженная пылинка (или молекула газа), попадает в какую-то точку электростатического поля. Объясните, что будет происходить с пылинками с точки зрения того, как меняться потенциал и потенциальная энергия при их перемещении. Проведите аналогию с упругим мячиком, попавшим в яму. Сделайте заключение о том, какой вид движения будет у пылинок (равномерный, равноускоренный, равнозамедленный).
Введите в командное окно MATLAB програму 6.
Изучите, какой вид будут иметь потенциальная диаграмма (фигура 1), семейство эквипотенциальных линий (фигура 2) и картина линий напряженности поля (фигура 3), в случае, когда электростатическое поле создается линейной системой (расположены на линии) положительных зарядов.
Програма 6.
clear;
e=1.6*10^-16;
R0=10^-6;
N=50;
i=1:N;
q(i)=e;
x1=-5*R0;
x2=5*R0;
xq(i)=x1+(x2-x1)/N*i;
yq(i)=0;
N1=23;
Xmin=-10*R0;
Ymin=-10*R0;
Xmax=10*R0;
Ymax=10*R0;
i=1:N1+1;
X(i)=Xmin+(Xmax-Xmin)/N1*(i+1);
j=1:N1+1;
Y(j)=Ymin+(Ymax-Ymin)/N1*(j+1);
M(i,j)=Potential(q,xq,yq,X,Y);
[X1,Y1]=meshgrid(X,Y);
[px,py]=gradient(-M,0.1,0.1);
px1=px./(px.^2+py.^2).^0.5;
py1=py./(px.^2+py.^2).^0.5;
surf(X1,Y1,M);
figure(2);
[C,h]=contour(X1,Y1,M);
clabel(C,h)
colormap cool
figure(3);
quiver(X1,Y1,px1,py1,0.6)
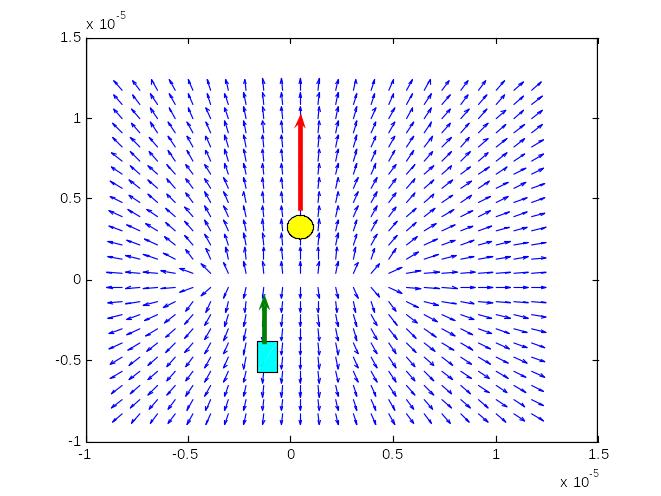
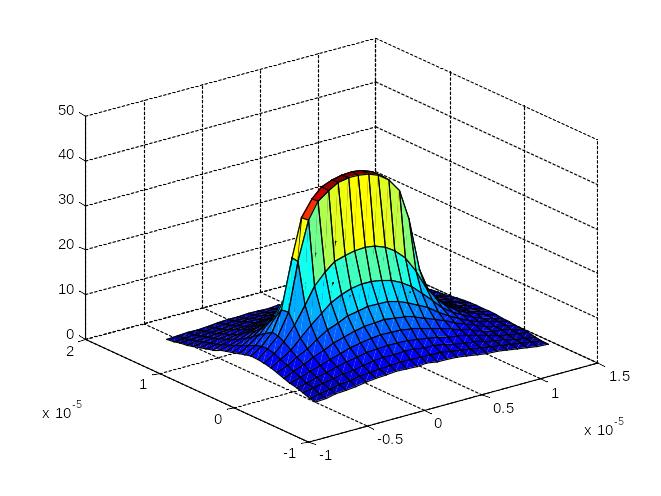
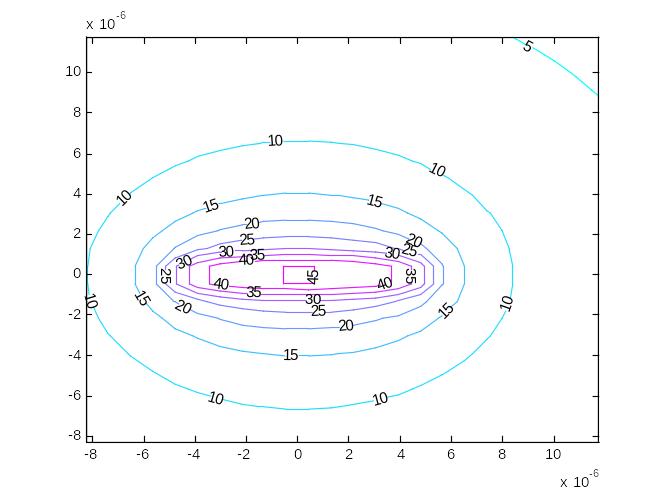
Кратко опишите, какие типичные фрагменты структуры электрического поля имеются в картине силовых линий изучаемой системы зарядов (является ли везде поле однородным)?
На основании картины линий напряженности электрического поля и знака у потока силовых линий, сделайте заключение о том, какие заряды являются источниками, а какие стоками.
Представьте, что в полученное графически электростатическое поле в какую-то его точку попадает пылинка (или молекула газа), имеющая положительный заряд. Отметьте на картине силовых линий аттрактор, его бассейн и сепаратриссу. Объясните, что будет происходить с пылинкой имеющей положительный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Представьте, что в какую-то точку исследуемого электростатического поля попадает пылинка (или молекула газа), имеющая отрицательный заряд. Объясните, что будет происходить с пылинкой имеющей отрицательный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Сделайте вывод о том, какой вид имеет потенциальная диаграмма изучаемой системы зарядов; выполняется ли условие, что потенциал системы зарядов на бесконечности стремиться к нулю.
Фигура 1 позволяет понять, что значит термин– потенциальный барьер. Потенциальная диаграмма представляет собой некое возвышение, распределенное вдоль одной координаты. Его и называют барьером. Согласно наших обычных представлений, можно говорить о том, что всякая положительно заряженная частица, подходя к барьеру со стороны его широкой части сможет преодолеть его, если ей удастся «перепрыгнуть» через него. Если полная энергия такой частицы меньше энергии гребня потенциального барьера, то, если судить по расположению стрелок, характеризующих действие силы на пробный единичный положительный заряд, положительно заряженная частица остановится и повернет обратно. То есть она не сможет пройти сквозь барьер. Преодолеть барьер («перепрыгнуть» его) может лишь та частица, которая обладает достаточно большой энергией (движется выше гребня барьера).
Несколько позже мы познакомимся с тем, что вопреки нашим представлениям, обусловленным классической механикой, в квантовой механике если барьер очень узок, то частица сможет с определенной вероятностью пройти сквозь барьер (как бы по туннелю). Это явление преодоления узкого потенциального барьера называют туннельным эффектом. Причины такого парадоксального поведения заряженной частицы – в волновых свойствах частиц малой массы (микрочастиц).

Какую форму на плоскости представляет семейство эквипотенциальных линий? (Имейте при этом в виду, что из-за погрешностей расчетов отдельные кривые в точке расположения заряда состоят из прямоугольных отрезков и лишь по мере отдаления от него приближаются к системе кругов разных радиусов).
Анализируя потенциальную диаграмму (фигура 1) и семейство эквипотенциальных линий, определите, в каком направлении наиболее быстро меняется потенциал.
Введите в командное окно MATLAB програму 7.
Изучите, какой вид будут иметь потенциальная диаграмма (фигура 1), семейство эквипотенциальных линий (фигура 2) и картина линий напряженности поля (фигура 3), в случае, когда электростатическое поле создается линейной системой (расположены на линии) отрицательных зарядов.
Програма 7.
clear;
e=1.6*10^-16;
R0=10^-6;
N=50;
i=1:N;
q(i)=-e;
x1=-5*R0;
x2=5*R0;
xq(i)=x1+(x2-x1)/N*i;
yq(i)=0;
N1=23;
Xmin=-10*R0;
Ymin=-10*R0;
Xmax=10*R0;
Ymax=10*R0;
i=1:N1+1;
X(i)=Xmin+(Xmax-Xmin)/N1*(i+1);
j=1:N1+1;
Y(j)=Ymin+(Ymax-Ymin)/N1*(j+1);
M(i,j)=Potential(q,xq,yq,X,Y);
[X1,Y1]=meshgrid(X,Y);
[px,py]=gradient(-M,0.1,0.1);
px1=px./(px.^2+py.^2).^0.5;
py1=py./(px.^2+py.^2).^0.5;
surf(X1,Y1,M);
figure(2);
[C,h]=contour(X1,Y1,M);
clabel(C,h)
colormap cool
figure(3);
quiver(X1,Y1,px1,py1,0.6)
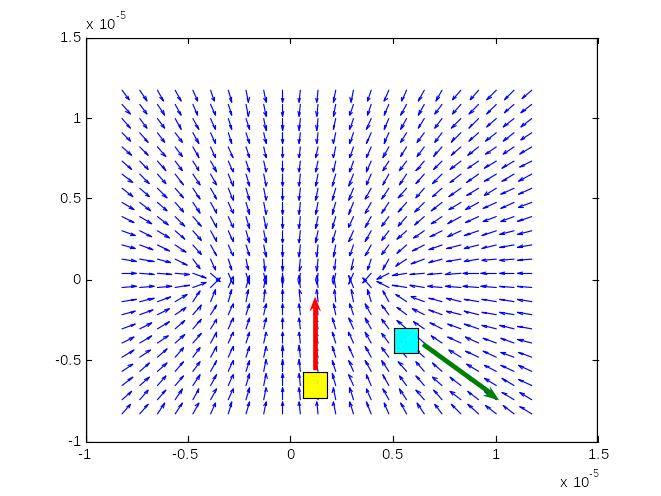

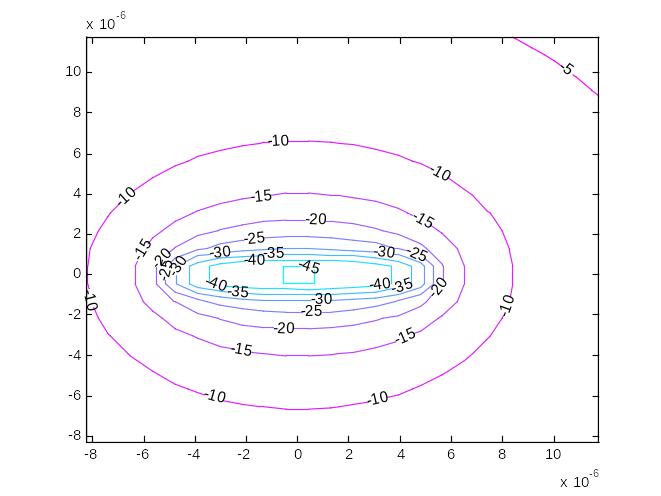
Кратко опишите, какие типичные фрагменты структуры электрического поля имеются в картине силовых линий изучаемой системы зарядов (является ли везде поле однородным)?
На основании картины линий напряженности электрического поля и знака у потока силовых линий, сделайте заключение о том, какие заряды являются источниками, а какие стоками.
Представьте, что в полученное графически электростатическое поле в какую-то его точку попадает пылинка (или молекула газа), имеющая положительный заряд. Отметьте на картине силовых линий аттрактор, его бассейн и сепаратриссу. Объясните, что будет происходить с пылинкой имеющей положительный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Представьте, что в какую-то точку исследуемого электростатического поля попадает пылинка (или молекула газа), имеющая отрицательный заряд. Объясните, что будет происходить с пылинкой имеющей отрицательный заряд в электростатическом поле с точки зрения попадания и непопадания ее в бассейн аттракции.
Сделайте вывод о том, какой вид имеет потенциальная диаграмма изучаемой системы зарядов; выполняется ли условие, что потенциал системы зарядов на бесконечности стремиться к нулю.
Фигура 1 позволяет понять, что означает термин– потенциальная яма.
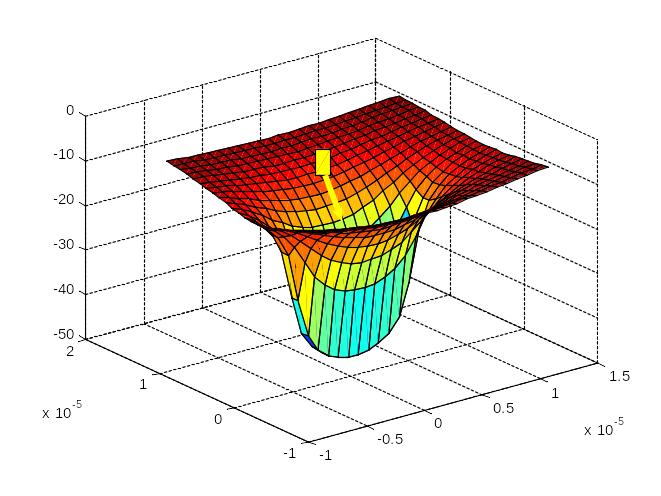
Потенциальная диаграмма в этом случае представляет собой некое углубление, распределенное вдоль одной координаты. Его и называют потенциальной ямой. Происхождение названия ясно из рисунка. Пока единичный положительный заряд находится вблизи системы линейно расположенных зарядов на него действуют силы, возвращающие его АО внутреннюю область. Если заряженная отрицательно пылинка, находящаяся в «яме», попытается «выбраться наружу», то силы будут отталкивать ее внутрь. Если полная энергия такой частицы меньше энергии, достаточной для того, чтобы «подняться из ямы» то положительно заряженная частица, даже обладающая начальной скоростью «вылета» остановится и повернет обратно в яму. То есть она не сможет выйти и потенциальной ямы. Выйти из ямы может лишь та частица, которая обладает достаточно большой энергией (имела достаточно высокую начальную скорость).
Какую форму на плоскости представляет семейство эквипотенциальных линий? (Имейте при этом в виду, что из-за погрешностей расчетов отдельные кривые в точке расположения заряда состоят из прямоугольных отрезков и лишь по мере отдаления от него приближаются к системе кругов разных радиусов).
Анализируя потенциальную диаграмму (фигура 1) и семейство эквипотенциальных линий, определите, в каком направлении наиболее быстро меняется потенциал.
Надо иметь в виду, что в широко используемых в настоящее время flash-накопителях информации, называемых просто «флэшками» запись единицы информации осуществляется за счет того, что заряд проникает через потенциальный барьер и «оседает» в потенциальной яме. Эти устройства конструируются таким образом. Что заряд может хранится в «яме» сроком до 10 лет.
В заключение отметим, что изученные свойства электростатического поля находят широкое применение в практической жизни и в промышленности. В частности, воздействие электростатического поля на заряженные тела позволяет решать ряд насущных технологических задач.
Широкое развитие получили технологии, которые включают три основных процесса: электризацию вещества, формирование движения в электрическом поле и распределение готового продукта. Взаимодействие заряженных частиц с электрическим полем используют.
1. В электрогазоочистке, для выделения из газового (воздушного) потока твердых тел или жидких частиц.
Например, в электрофильтрах на пылинки запыленного газа предварительно за счет ионизации «наносят» отрицательный заряд. Во время движения в электростатическом поле вблизи положительно заряженного электрода отрицательно заряженные пылинки движутся к положительному электроду и оседают на нем. Осадительный электрод периодически встряхивается и осевшая пыль ссыпается в бункер, а затем удаляется.
Созданы и успешно применяются электрофильтры для улавливания пыли, которая содержит серебро, медь, никель, цинк, свинец, магний и другие металлы. Трудно переоценить экологический эффект от использования электрофильтров для улавливания частиц в дымовых газах тепловых электростанций, котелен, предприятий металлургической промышленности, которые выбрасывают в воздух огромное количество всевозможных газов, загрязняющих атмосферу и окружающую среду. Созданы и успешно применяются электрофильтры для очистки воздуха в животноводческих помещениях и на птицефабриках с большой запыленностью и бактерицидностью. Некоторые агрегаты улавливаю 90 % пылевых частиц и 80 % микроорганизмов при потребляемой мощности всего 0,7 Вт.
2. Для электросепарации – разделения многокомпонентных частиц на составные части.
Например, в зерноочистительных машинах семена заряжаются и ориентируются вдоль силовых линий поля. Имея различную массу, семена при перемещении в электростатическом поле отклоняются (отрываются) в разных местах и «направляются» по различным ячейкам приемного бункера, поскольку степень перемещения их зависит от вида семян и их электрофизических свойств. Это позволяет из одной и той же партии семян выделить фракции с однородными качественными показателями.
3. Для электроокраски – нанесения твердых и жидких покрытий (красок) на изделия.
Например, в установках электростатической окраски вдуваемые пневматическим распылителем частицы краски заряжаются и превратившись в отрицательные ионы, движутся к положительно заряженным изделиям. Заряженные частицы попадают на изделие со всех сторон и равномерно плотным слоем краски окрашивают всю его поверхность.
Эксперимент 2. Изучение посредством моделирования основных понятий, связанных со стационарным магнитным полем.
Вы уже имеете опыт общения с магнитными полями. Наверняка Вы проводили простейший эксперимент, когда берут два постоянных магнита и сближают (или удаляют) их полюсы. Этот опыт демонстрировал, что в пространстве между полюсами имеется силовое поле, позволяющее магнитам бесконтактно взаимодействовать. Вы убедились в том, что какие-то невидимые глазу силы притягивали или отталкивали два твердых тела.
Надо заметить, что, вообще говоря, люди давно имели представление о магнитах и наличии у них силовых полей, позволяющих осуществлять телам бесконтактное взаимодействие. История магнетизма изобилует многими любопытными сюжетами.
Так еще Тит Лукреций Кар в своей книге «О природе вещей» писал:
«Мне остается сказать, по какому закону природы
Может железо к себе притягивать камень, который
Греки «магнитом» зовут по названию месторождения,
Ибо находится он в пределах отчизны магнетов…»
Считается, что китайцы использовали компас с магнитами уже около 2500 г. до н.э. Возможно это и не так, но то, что Фалесу Милетскому в шестом столетии до нашей эры было известно о притяжении магнитного железняка к железу, не вызывает сомнения. Уильям Гильберт написал в 1600 г., что «по счастливой случайности плавильщики железа или рудокопы открыли магнетизм еще в 800 г. до н. э.».
В школе вы достаточно подробно знакомились с магнитами и полями, которые ими создаются. В частности, наглядным является опыт с металлическими опилками, который свидетельствует о том, что есть некие силы, которые ориентируют опилки строго определенным образом (рис.5).

Рис. 5. Графическое изображение картины магнитного поля, полученное при помощи железных опилок
Вам также известно, что магнитное поле может быть создано не только постоянными магнитами, но и движущимися электрическими зарядами.
По аналогии с основной характеристикой
электрического поля – напряженностью
,
которая определяется через силу,
действующую на заряд, для описания
магнитного поля используют тоже
действующий на заряд вектор
![]() ,
который называют магнитной индукцией.
Подчеркнем, что количественная
характеристика магнитного поля
,
который называют магнитной индукцией.
Подчеркнем, что количественная
характеристика магнитного поля
![]() аналогична напряженности электрического
поля
только в том смысле, что, как напряженность
,
так и магнитная индукция
определяют силу, действующую на заряд.
аналогична напряженности электрического
поля
только в том смысле, что, как напряженность
,
так и магнитная индукция
определяют силу, действующую на заряд.
Хотя вводимые для описания полей векторы и формально сходны, Вам говорили, что магнитное поле действует на заряд совсем не так, как электрическое. Магнит не притягивает и не отталкивает электрический заряд, а действует на него в направлении перпендикулярном к полю и к скорости заряда.
Кроме того, как показывает опыт, магнитное поле на неподвижные заряды вообще не действует. Для того, чтобы на заряд со стороны магнитного поля действовала сила, требуется, чтобы он двигался (и притом не параллельно вектору ,как это было в случае электрического поля, иначе сила снова-таки обращается в нуль).
Действие магнитного поля на движущийся заряд определяется формулой магнитной силы Лоренса
![]() ,
,
где – коэффициент пропорциональности, зависящий от выбора системы единиц;
-величина заряда;
![]() -
магнитная индукция;
-
магнитная индукция;
![]() -
скорость заряда;
-
скорость заряда;
![]() - угол между направлением скорости
заряда и вектором магнитной индукции
.
- угол между направлением скорости
заряда и вектором магнитной индукции
.
Сила Лоренса направлена перпендикулярно
к плоскости, в которой находятся вектор
и скорости заряда![]() .
При этом максимального значения сила
Лоренца достигает тогда, когда вектор
скорости заряда перпендикулярен вектору
магнитной индукции
.
.
При этом максимального значения сила
Лоренца достигает тогда, когда вектор
скорости заряда перпендикулярен вектору
магнитной индукции
.
Статическое магнитное поле удобно изображать графически с помощью картины так называемых силовых магнитных линий.
Линией вектора магнитной индукции (магнитной силовой линией) называется линия (помеченная стрелочкой), касательная к которой в каждой точке пространства (поля) совпадает с направлением магнитной индукции .
Магнитное поле может быть также создано электрическими зарядами, которые движутся в проводнике, создавая электрический ток (вспомните: ток это есть упорядоченное движение зарядов).
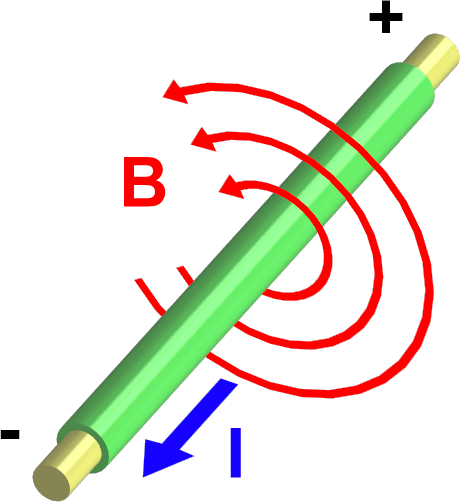
Рис. 5. Графическое изображение картины магнитного поля для тонкого прямого провода с током. Ток (I), протекая через провод, создаёт магнитное поле вокруг провода, которое можно характеризовать в виде замкнутых линий магнитной индукции В
Заметим, что наглядно демонстрировать в пространстве картину магнитного поля , даже представляемую замкнутыми магнитными линиями, весьма сложно. Поэтому, чтобы получить наглядное и удобное для анализа графическое изображение, замкнутые магнитные линии чаще всего проецируют на плоскость так, чтобы получались наглядные плоские картины.
Вам демонстрировали, что если на листе картона вокруг проводника, перпендикулярно пронизывающего плоскость картона, разместить маленькие магнитные стрелки, то при включении сильного электрического тока стрелки расположатся по касательным к окружности с центром в точке, где проводник пересекает картон. Это свидетельствует о том, что силовые линии вектора прямого проводника с током являются окружностями.
В частности, если ток, создающий магнитное поле, течет по очень тонкому прямому проводнику, пересекающему перпендикулярную к нему плоскость, то оставшийся в виде точки след на плоскости будут окружать замкнутые в виде окружностей линии магнитного поля , что является весьма наглядным.
Данный факт очень важен. Оказывается, что линии вектора магнитной индукции всегда замкнуты. Замкнутые линии нигде не начинаются и нигде не кончаются. Этим они отличаются от линий напряженности электрического поля, создаваемого источниками или стоками.
Замкнутость линий вектора
означает, что в природе не существует
магнитных зарядов. А поскольку
магнитных зарядов нет, (в отличие от
существующих в природе электрических),
то вектор
не имеет ни источников ни стоков. Если
Вы вспомните, как мы определяли понятия
стока и истока, то, несомненно, сразу
определите, что для магнитного поля
имеет место дивергенция равная нулю
![]() .
.
Поля, имеющие структуру, когда векторные линии нигде не начинаются и не кончаются, а замыкаются вокруг электрических токов, называют соленоидальными.
Соленоидальные поля создаются вихрями. В частности, можно говорить, что электрические токи служат вихрями вектора . В случае с проводником тока вихрем поля будет линия, по которой протекает ток и вокруг которой замыкаются линии поля.
Обратим внимание, что вихри, создающие магнитное поле, характеризуются свое величиной и направлением (например, проводник с током может быть по-разному ориентирован в пространстве и иметь различное направление протекания тока). Источники, как Вы помните, характеризуются только своей величиной; направления они, разумеется, не имеют. Иными словами, источники являются скалярными величинами, а вихри – векторными. Элементарным источником естественно считать точечный заряд, а элементарным вихрем - тонкий проводник в виде прямой линии.
Вихри могут быть линейными, поверхностными или объемными. Примером линейного вихря магнитного поля может служить тонкий проводник с током. Макротоки и микротоки, текущие по поверхности проводника различной формы являются поверхностными вихрями вектора . Проводник с током, имеющий большое сечение представляет собой объемный вихрь вектора .
Соленоидальность поля и равенство нулю дивергенции требует по-новому взглянуть на свойства магнитного поля.
Во-первых, оказывается, что никак нельзя утверждать, что работа на любом замкнутом пути равна нулю, если силовые линии имеют вид окружности. В вихревом поле существуют такие замкнутые пути, на которых работа (циркуляция) не равна нулю. Следовательно, вихревое поле не является потенциальным.
В осмыслении последнего факта нам поможет введение нескольких понятий из векторного анализа.
Пусть , и - проекции вектора на оси координат Ох, Оy, Oz соответственно, то есть задано векторное поле
![]() .
.
Будем считать также, что в этой области
расположена гладкая или кусочно-гладкая
кривая
![]() .
Выберем на кривой
одно из двух направлений движения и
обозначим через
.
Выберем на кривой
одно из двух направлений движения и
обозначим через
![]() вектор, имеющий в каждой точке направление,
совпадающее с направлением движения
по кривой в этой точке, а по модулю равный
дифференциалу длины дуги:
вектор, имеющий в каждой точке направление,
совпадающее с направлением движения
по кривой в этой точке, а по модулю равный
дифференциалу длины дуги:
![]() .
.
Тогда криволинейный интеграл от
скалярного произведения векторов
![]() и
и
![]()
называется циркуляцией векторного поля вдоль кривой . В силовом поле циркуляция выражает работу силового поля при перемещении материальной точки вдоль пути .
Итак, первое, мерой мощности полного вихря (заключенного в контуре) принято считать величину циркуляции вектора по данному контуру (работу силового поля, а не дивергенцию, как это было в случае электростатического поля).
Во-вторых, важным свойством соленоидального поля является его ротация.
Пусть опять , и - проекции вектора на оси координат Ох, Оy, Oz соответственно, и опять задано векторное поле
.
Тогда мерой ротации является векторная
величина называемая ротором и
обозначаемая символом
![]() .
Величина ротора векторного поля равна
.
Величина ротора векторного поля равна
 .
.
Ротор называют еще вихрем. Это
название еще связано с тем, что он как
бы «смешивает» производные и компоненты.
Он как бы «следит» за тем, как меняются
компоненты векторного поля
![]() в «чужих» направлениях. Таким образом,
ротор – это некая мера вращения
векторного поля.
в «чужих» направлениях. Таким образом,
ротор – это некая мера вращения
векторного поля.
Если Вы взглянете на картину
электростатического поля электрического
заряда, то увидите, что вращение поля
отсутствует. Следовательно, не делая
громоздких математических преобразований,
можно утверждать, что для всякого
потенциального поля
![]() .
Другими словами – потенциальное поле
является безвихревым. С другой стороны,
мы уже отмечали, что у соленоидального
стационарного магнитного поля
.
.
Другими словами – потенциальное поле
является безвихревым. С другой стороны,
мы уже отмечали, что у соленоидального
стационарного магнитного поля
.
Если плотность протекающего тока
![]() заданная величина, где
-
сечение проводника то стационарное
магнитное поле может быть определено
из решения системы уравнений
заданная величина, где
-
сечение проводника то стационарное
магнитное поле может быть определено
из решения системы уравнений

где
![]() -вектор напряженности магнитного поля.
-вектор напряженности магнитного поля.
Заметим, что вектор определяет магнитное поле, создаваемое только токами проводимости, а вектор - магнитное поле, создаваемое, как токами проводимости, так и имеющимися намагниченными телами.
Решение этой системы уравнений дает
так называемый обобщенный закон
Био-Савара, который позволяет вычислить
магнитную индукцию, создаваемую
элементом постоянным тока
![]() ,
расположенным в точке с радиус-вектором
,
в точке наблюдения с радиус – вектором
,
расположенным в точке с радиус-вектором
,
в точке наблюдения с радиус – вектором
![]()
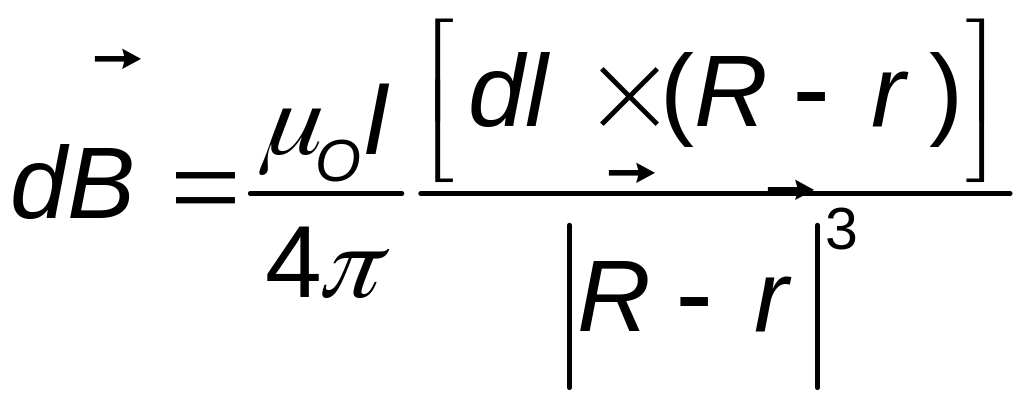 ,
,
где
![]() -
величина тока,
-
величина тока,
![]() -магнитная
проницаемость.
-магнитная
проницаемость.
Вычислить магнитное поле аналитически (то есть получить результат в виде формулы) оказывается возможным для структур, имеющих достаточно высокую степень симметрии (прямой провод, поле кольца на оси симметрии). Для большинства структур расчет может быть проведен только численно.
Удобно для расчетов ввести векторную
величину
,
называемую векторным потенциалом,
которая связана с вектором магнитной
индукции
следующим образом
![]() .
То есть величину, ротор которой дает
возможность определить магнитное поле.
Это позволяет находить магнитное поле
в два приема. Сначала находится векторный
потенциал
,
а затем определяется
.
Для целого класса задач и в ряде случаев
такой путь анализа оказывается менее
трудоемким, чем непосредственное
применение закона Био- Савара.
.
То есть величину, ротор которой дает
возможность определить магнитное поле.
Это позволяет находить магнитное поле
в два приема. Сначала находится векторный
потенциал
,
а затем определяется
.
Для целого класса задач и в ряде случаев
такой путь анализа оказывается менее
трудоемким, чем непосредственное
применение закона Био- Савара.
Если силовая магнитная линия, есть линия
на которой
![]() ,
то для построения такой линии достаточно
вычислить модуль векторного потенциала
в узлах координатной сетки и затем
построить карту магнитных эквипотенциалей.
,
то для построения такой линии достаточно
вычислить модуль векторного потенциала
в узлах координатной сетки и затем
построить карту магнитных эквипотенциалей.
Введите в командное окно MATLAB програму 8.
Изучите, какой вид будут иметь картина магнитного поля в случае если его вихрем является петля с постоянным током (круговой ток в плоскости ху).
Програма 8.
clear;
N1=21;
i=1:N1+1;
Ymin=-5;
Ymax=5;
Zmin=-5;
Zmax=5;
Y(i)=Ymin+(Ymax-Ymin)/N1*(i-1);
Z(i)=Zmin+(Zmax-Zmin)/N1*(i-1);
a=1;
Nstep=100;
X=0;
Ny=length(Y);
Nz=length(Z);
deltaphi=2*pi/Nstep;
n=1:Nstep+1;
phi(n)=deltaphi*(n-1);
for i=1:Nz
for j=1:Ny
s=[0 0 0];
for n=1:Nstep+1
dL=[-a*sin(phi(n))*deltaphi a*cos(phi(n))*deltaphi 0];
r=[a*cos(phi(n)) a*sin(phi(n)) 0];
R=[X Y(j) Z(i)];
s=s+cross(dL,(R-r))./((R-r)*(R-r)').^(3/2);
end
by(i,j)=s(2);
bz(i,j)=s(3);
end;
end;
By=by;
Bz=bz;
mp1=(by.^2+bz.^2).^0.5;
by1=by./mp1;
bz1=bz./mp1;
quiver(Y,Z,by1,bz1,0.6);
Nstep=100;
X=0;
Ny=length(Y);
Nz=length(Z);
deltaphi=2*pi/Nstep;
n=1:Nstep+1;
phi(n)=deltaphi*(n-1);
for i=1:Nz
for j=1:Ny
s=[0 0 0];
for n=1:Nstep+1
dL=[-a*sin(phi(n))*deltaphi a*cos(phi(n))*deltaphi 0];
r=[a*cos(phi(n)) a*sin(phi(n)) 0];
R=[X Y(j) Z(i)];
s=s+dL./((R-r)*(R-r)').^(1/2);
end
bx(i,j)=s(1);
by(i,j)=s(2);
bz(i,j)=s(3);
end;
end;
mp=(bx.^2+by.^2+bz.^2).^0.5;
yi=Ymin:(Ymax-Ymin)/1000:Ymax;
zi=Zmin:(Zmax-Zmin)/1000:Zmax;
[y1 z1]=meshgrid(Y,Z);
[y2 z2]=meshgrid(yi,yi);
zi3=interp2(y1,z1,mp,y2,z2,'bicubic');
figure (2)
contour (yi,zi,zi3,55);
Чтобы было легче ориентироваться в получаемых изображениях, следует иметь в виду, что круговой виток, по которому протекает ток, расположен в горизонтальной плоскости хОу при z=0. Ось Оz проходит через центр кругового тока. Фигуры, получаемые в результате компьютерного расчета, представляют изображение в плоскости yOz при х =0 (в этом случае магнитные силовые линии лежат в плоскости, перпендикулярной плоскости витка). Виток при таком рассмотрении на фигурах будет представлять две точки, расположенные на оси Оу на удалении от центра на величину, равную радиусу витка. Магнитное поле визуализируется (представляется в виде изображения) так, что мы видим составляющие вектора магнитной индукции, расположенные в плоскости yOz.
На
фигуре 1 изображен набор векторов
![]() ,
характеризующих в деталях расположение
векторов
,
то есть структуру магнитного поля. Эти
векторы являются касательными к силовым
линиям магнитного поля.
,
характеризующих в деталях расположение
векторов
,
то есть структуру магнитного поля. Эти
векторы являются касательными к силовым
линиям магнитного поля.
Фигура 2 демонстрирует карту силовых линий магнитного поля. Направление силовых линий кругового поля зависит от направления электрического тока в проводнике и определяется так называемым правилом «буравчика». Если буравчик мысленно ввинчивать по направлению тока, то направление вращения его ручки будет совпадать с направлением магнитных силовых линий поля. Применяя это правило, можно узнать направление тока в проводнике, если известно направление силовых линий поля, созданного этим током.
Если
в магнитное поле
попадает движущаяся со скоростью
заряженная частичка
,
то на нее будет воздействовать сила
![]() .
Эта сила перпендикулярна векторам
и
,
которая будет искривлять траекторию
движения частицы.
.
Эта сила перпендикулярна векторам
и
,
которая будет искривлять траекторию
движения частицы.
На основании анализа изображений, получаемых путем визуализации структуры магнитного поля и его магнитных силовых линий, сделайте выводы о следующем.
Какую форму на плоскости имеет семейство замкнутых силовых линий магнитной напряженности, характеризующих вектор магнитной индукции? Имеет ли магнитное поле кругового витка с током стоки и истоки?
Имеются в картине силовых линий ротация, свидетельствующая о наличии вихрей магнитного поля. Сформулируйте, является ли исследуемое магнитное поле кругового витка с током потенциальным или соленоидальным.
На основании картины линий напряженности магнитного поля сделайте заключение о том, что будет происходить, если слева в представленное графически магнитное поле влетает пылинка (или молекула газа), имеющая положительный заряд.
Объясните, что будет происходить в статическом магнитном поле с пылинкой (или молекулой газа), имеющей отрицательный заряд, если она влетает слева в представленное графически магнитное поле.
Измените радиус витка,
сделав его, вместо
![]() ,
равным
,
равным
![]() .
Опишите, в главных чертах, как изменилась
картина магнитного поля.
.
Опишите, в главных чертах, как изменилась
картина магнитного поля.
В реальной жизни чаще приходится иметь дело не с одним круговым витком, а их набором, с различного рода катушками, состоящими из ряда витков (рис. 6) или так называемыми соленоидами. Так называемый соленоид образует ряд витков, имеющий форму спирали.
Соленоид – это катушка индуктивности в виде намотанного на цилиндрическую поверхность изолированного проводника, по которому течёт электрический ток. Электрический ток в обмотке создает в окружающем пространстве магнитное поле соленоида.

Рис. 6. Катушки, состоящие из набора круговых витков
Сила магнитного поля катушки с током зависит от числа витков катушки, от силы тока в цепи и от наличия сердечника в катушке. Чем большее число витков в катушке и чем больше сила тока, тем сильнее магнитное поле. Железный сердечник (рис. 7), введенный внутрь катушки с током, усиливает магнитное поле катушки.
Рис. 7. Соленоид, внутрь которого введен сердечник
Вокруг соленоида, при прохождении через него тока, образуется магнитное поле (рис.8). Несмотря на то, что ток в соленоиде движется по спирали можно считать соленоид эквивалентным пачке плотно примкнувших друг к другу токовых колец. Магнитное поле соленоида получается в результате сложения магнитных полей каждого витка и по форме напоминает магнитное поле прямолинейного магнита.
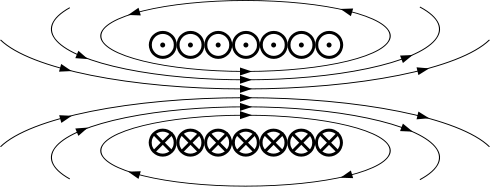
Рис. 8. Соленоид, состоящий из круговых витков: крестики внизу указывают на то, что ток вытекает, а токи вверху – что втекает
Силовые линии магнитного поля соленоида, так же как и в прямолинейном магните, выходят из одного конца соленоида и возвращаются в другой. Внутри соленоида они имеют одинаковое направление. Линии магнитного поля по-прежнему не имеют ни начала, ни конца и проходят сквозь центральную область соленоида, направляясь вне соленоида от северного полюса к южному, а внутри соленоида от южного полюса к северному
Концы соленоида обладают полярностью (рис.9, рис.10). Тот конец, из которого выходят силовые линии, является северным полюсом соленоида, а конец, в который силовые линии входят, — его южным полюсом.

Рис. 9. Подобие магнитных полей соленоида и постоянного магнита

Рис. 10. Полюса соленоида обладают полярностью
Полюса соленоида можно определить по правилу правой руки, но для этого надо знать направление тока в его витках. Если наложить на соленоид правую руку ладонью вниз, так чтобы ток как бы выходил из пальцев, то отогнутый большой палец укажет на северный полюс соленоида. Из этого правила следует, что полярность соленоида зависит от направления тока в нем. В этом нетрудно убедиться практически, поднеся к одному из полюсов соленоида магнитную стрелку и затем изменив направление тока в соленоиде. Стрелка моментально повернется на 180°, т. е. укажет на то, что полюсы соленоида изменились.
Изученные свойства стационарного магнитного поля находят широкое применение в практической жизни и в промышленности.
1. В частности, соленоид обладает свойством втягивать в себя легкие железные предметы. Если внутрь соленоида поместить стальной брусок, то через некоторое время под действием магнитного поля соленоида брусок намагнитится. Этот способ применяют при изготовлении электромагнитов. Полюсы электромагнита, как и соленоида, определяются по правилу правой руки. Если в обмотке электромагнита изменить направление тока, то в соответствии с этим изменится и полярность электромагнита.
Электромагнит представляет собой устройство (соленоид с помещенным внутрь нее железным сердечником), создающее магнитное поле при прохождении электрического тока, предназначенное для создания механического усилия.
Формы и размеры электромагнитов разнообразны, однако общее устройство всех их одинаково. Обычно электромагнит состоит из обмотки (катушки) и магнитопровода (ферромагнитного сердечника), который приобретает свойства магнита при прохождении по обмотке тока. В электромагнитах, предназначенных, прежде всего, для создания механического усилия также присутствует якорь (подвижная часть), передающий усилие. Обмотку электромагнитов изготавливают из изолированного алюминиевого или медного провода.
Катушка электромагнита представляет собой каркас имеющий различные формы в зависимости от назначения электромагнита. На каркас намотана в несколько слоев медная изолированная проволока — обмотка электромагнита. Она имеет различно число витков и изготовляется из проволоки различного диаметра, в зависимости от назначения электромагнита. Для предохранения изоляции обмотки от механических повреждений обмотку покрывают одним или несколькими слоями бумаги или каким-либо другим изолирующим материалом. Начало и конец обмотки выводят наружу и присоединяют к выводным клеммам, укрепленным на каркасе, или к гибким проводникам с наконечниками на концах.
Катушка электромагнита насажена на магнитопровод, который изготавливают из магнитно-мягких материалов — обычно из электротехнической или качественной конструкционной стали, литой стали и чугуна, железоникелевых и железокобальтовых сплавов. Для снижения потерь на вихревые токи (токи Фуко) магнитопроводы выполняют делают составными из тонких листов, изолированных друг от друга. Формы сердечников могут быть различными, в зависимости от назначения электромагнита.
Если по обмотке электромагнита пропустить электрический ток, то вокруг обмотки образуется магнитное поле, которое намагничивает сердечник. Так как сердечник сделан из мягкого железа, то он намагнитится мгновенно. Если затем выключить ток, то магнитные свойства сердечника также быстро исчезнут, и он перестанет быть магнитом (рис.11).

Рис. 11. Простейшая конструкция электромагнита. При прохождении тока скрепка будет притянута к сердечнику, выполненному в виде винта
Сила же притяжения электромагнита не является величиной постоянной. Один и тот же электромагнит может обладать различной силой притяжения.
Сила притяжения электромагнита зависит от величины тока, проходящего через обмотку этого электромагнита. Чем больше ток, тем больше сила притяжения электромагнита, и, наоборот, чем меньше ток в обмотке электромагнита, тем с меньшей силой он притягивает к себе магнитные тела.
Кроме того, сила его притяжения электромагнита будут тем больше, чем большее количество витков имеет обмотка. Если, например, взять два электромагнита одинакового устройства и размеров, но один с небольшим числом витков обмотки, а другой — с гораздо большим, то нетрудно убедиться, что при одном и том же токе сила притяжения последнего будет гораздо больше. Действительно, чем больше число витков обмотки, тем большее при данном токе создается вокруг этой обмотки магнитное поле, так как оно слагается из магнитных полей каждого витка. Значит, магнитный поток электромагнита, а, следовательно, и сила его притяжения будут тем больше, чем большее количество витков имеет обмотка.
Есть еще одна причина, влияющая на величину магнитного потока электромагнита. Это — качество его магнитной цепи. Магнитной цепью называется путь, по которому замыкается магнитный поток. Магнитная цепь обладает определенным магнитным сопротивлением. Магнитное сопротивление зависит от магнитной проницаемости среды, через которую проходит магнитный поток. Чем больше магнитная проницаемость этой среды, тем меньше ее магнитное сопротивление. Так как магнитная проницаемость ферромагнитных тел (железа, стали) во много раз больше магнитной проницаемости воздуха, поэтому выгоднее делать электромагниты так, чтобы их магнитная цепь не содержала в себе воздушных участков. Произведение силы тока на число витков обмотки электромагнита называется магнитодвижущей силой. Магнитодвижущая сила измеряется числом ампер-витков. Например, по обмотке электромагнита, имеющего 1200 витков, проходит ток силой 50 мА. Магнитодвижущая сила такого электромагнита равна 0,05 х 1200 = 60 ампер-витков.
Число витков обмотки и магнитное сопротивление для каждого электромагнита есть величина постоянная. Поэтому магнитный поток данного электромагнита изменяется только с изменением тока, проходящего по обмотке. Так как сила притяжения электромагнита обусловливается его магнитным потоком, то, чтобы увеличить (или уменьшить) силу притяжения электромагнита, надо соответственно увеличить (или уменьшить) ток в его обмотке.
Большинство технических применений магнитов основывается на их способности притягивать и удерживать железные предметы. И в этих применениях электромагниты имеют огромные преимущества перед постоянными магнитами, ибо изменение силы тока в обмотке электромагнита позволяет быстро изменять его подъемную силу.
Сила, с которой магнит притягивает железо, резко убывает по мере увеличения расстояния между магнитом и железом. Поэтому для определенности подъемной силой магнита условились называть силу, с которой магнит удерживает железо, расположенное в непосредственной близости к нему; другими словами, подъемная сила магнита равна той силе, которая необходима, чтобы оторвать от магнита притянутый к нему кусок чистого мягкого железа.
Чтобы получить электромагнит с возможно большей подъемной силой, нужно увеличить площадь соприкосновения полюсов магнита с притягиваемым железным предметом и добиться того, чтобы линии магнитного поля проходили только в железе. Этим требованиям хорошо удовлетворяет конструкция так называемого горшкообразного магнита, изображенного на рис. 12. Такой электромагнит, питаемый аккумулятором или батареей от карманного фонаря, удерживает груз массы 80— 100 кг.
Рис. 12. Горшкообразный электромагнит в разобранном виде (а) и в разрезе (б): 1 — тело электромагнита, на выступ которого надевается обмотка 2, 3 — зажимы обмотки, 4 — якорь
Электромагниты с большой подъемной силой (рис.13) применяются в технике для весьма различных целей.
На заводах применяются электромагнитные подъемные краны, которые могут переносить огромные грузы без их крепления. Например, электромагнитный подъемный кран (рис.14) применяется на металлургических и металлообрабатывающих заводах для переноски железного лома (рис.15) и готовых изделий.

Рис. 13. Внешний вид электромагнитов с большой подъемной силой

Рис. 14. Внешний вид крана для транспортировки железного лома

Рис. 15. Внешний вид электромагнита для переноски железного лома
На металлообрабатывающих заводах часто применяют также станки с так называемыми магнитными столами, на которых обрабатываемое железное или стальное изделие закрепляется притяжением сильных электромагнитов. Достаточно включить ток, чтобы надежно закрепить изделие в любом положении на столе; достаточно выключить ток, чтобы освободить его.
При отделении магнитных материалов от немагнитных, например, при отделении кусков железной руды от пустой породы (обогащение руды), применяют магнитные сепараторы, в которых очищаемый материал проходит через сильное магнитное поле электромагнитов, вытягивающее из него все магнитные частицы.
Чтобы избежать несчастных случаев, связанных с отключением тока, а также с целью сэкономить потребление электрической энергии, при электромагнитах стали устраивать особые приспособления. После того как переносимые предметы подняты магнитом, сбоку опускаются и плотно закрываются прочные стальные подхватки, которые затем сами поддерживают груз, ток же во время транспортировки прерывается (рис.13).
В морских портах для перегрузки металлолома используются , наверное, самые мощные круглые грузоподъемные электромагниты. Их масса достигает 10 тонн, грузоподъемность до 64 тонн, а отрывное усилие до 128 тонн.
Перспективно использование электромагнитов на скоростных транспортных средствах для создания " магнитной подушки" (рис.15).
 или
или
Рис. 15. Использование электромагнита для создания транспортных средств
2. Широкое применение в практической жизни и в промышленности находят реле, использующие также свойства магнитных полей
Реле — электромагнитный аппарат (переключатель), предназначенный для коммутации электрических цепей (скачкообразного изменения выходных величин) при заданных изменениях электрических или не электрических входных величин. Реле широко используется в различных автоматических устройствах.
Работа электромагнитных реле основана на использовании электромагнитных сил, возникающих в металлическом сердечнике при прохождении тока по виткам его катушки. В конструкцию реле входят: электромагнит, якорь и переключатель (рис.16).
Электромагнит представляет собой электрический провод, намотанный на катушку с сердечником из магнитного материала. Якорь — пластина из магнитного материала, через толкатель управляющая контактами.

Рис. 15. Конструктивное исполнение реле
В исходном положении якорь удерживается пружиной. При пропускании электрического тока через обмотку электромагнита возникающее магнитное поле притягивает к сердечнику якорь, преодолевая усилие пружины, который через толкатель смещает и тем самым переключает контакты (замыкает или размыкает контакты в зависимости от конструкции реле). После отключения управляющего напряжения пружина возвращает якорь в исходное положение. Переключатели могут быть замыкающими, размыкающими, переключающими.
3. Для специальных целей строят электромагниты и других типов.
Врачи, например, применяют электромагниты для удаления из глаза случайно попавших в него железных опилок.
Для обжатия тонкостенных металлических труб с образованием резьбы, изготовления многогранных торцевых ключей из цилиндрических заготовок, соединения деталей напресовкой используются магнитоимпульсные установки для пластической деформации металлов и их сплавов непосредственно в установке.
Для транспортировки жидких металлов используются кондукционные насосы, которые предназначены для перекачивания проводящей жидкости под действием силы, возникающей при взаимодействии магнитного поля насоса и электрическим током, проходящим через находящуюся в насосе проводящую жидкость.
Магнитные поля используются в большом адронном коллайдере (англ. Large Hadron Collider, LHC; сокр. БАК) — ускорителе заряженных частиц на встречных пучках, предназначенном для разгона протонов и тяжёлых ионов (ионов свинца) и изучения продуктов их соударений. Коллайдер построен в научно-исследовательском центре Европейского совета ядерных исследований (фр. Conseil Européen pour la Recherche Nucléaire, CERN), на границе Швейцарии и Франции, недалеко от Женевы (рис.16). БАК является самой крупной экспериментальной установкой в мире. Большим назван из-за своих размеров: длина основного кольца ускорителя составляет 26 659 м; адронным — из-за того, что он ускоряет адроны, то есть частицы, состоящие из кварков; коллайдером (англ. collide — сталкиваться) — из-за того, что пучки частиц ускоряются в противоположных направлениях и сталкиваются в специальных точках столкновения
На глубине 100 метров по кольцу диаметром примерно 27 километров заряженные частицы будут разгоняться почти до скорости света. Будет воссоздана модель Большого взрыва, благодаря которому и появилась наша вселенная. Протонам предстоит столкнуться с невиданной доселе энергией – 14 терраэлектронвольт – в миллион раз больше, чем при единичном термоядерном синтезе. Сталкиваясь, они образуют миллионы осколков, которые и предстоит исследовать.
Рис. 16. Размещение адронного коллайдера на карте
С помощью БАК ученые надеются значительно продвинуться в понимании, откуда появилась материя и время. В большом андронном коллайдере физики хотят поймать бозон Хиггса, именуемый также «частицей Бога». На теоретическом обосновании ее существования строятся все современные теории происхождения вселенной. Если «частицу Бога» не найдут, все аккуратно выведенные физиками законы окажутся всего лишь неверными гипотезами.
Принцип работы большого андронного коллайдера состоит в следующем. Два луча субатомных частиц (андроны) будут двигаться навстречу друг другу, набирая с каждым кругом всё больше энергии. При этом для удержания и коррекции частиц используются 1624 сверхпроводящих магнита, которые работают при температуре -271 °C . Когда энергии будет достаточно, частицы столкнутся тем самым учёные создадут модель Большого взрыва. Появившиеся после взрыва частицы будут проанализированы учеными со всего мира. На рис. 17,18 показано конструктивное исполнение электромагнитов, которые используются для удержания частиц на заданной траектории.

Рис. 17. Фотография конструктивного исполнения сверхпроводящих магнита снаружи

Рис. 18. Фотография конструктивного исполнения сверхпроводящих магнита внутри
Эксперимент 3. Изучение посредством моделирования основных понятий, связанных полями, возникающими при движении жидкостей и газов.
Большинство процессов в технике и технологии связано с переносом в пространстве конкретных физических субстанций, в том числе жидкостей и газов. Тысячи лет люди наблюдают вечно изменчивое течение воды, газа (дыма) и пытаются разгадать их тайну. Первоклассные физики и математики ломали и продолжают ломать головы, стараясь понять природу и прихотливое поведение потоков воды и газа. Но вступив в XXI век, мы с сожалением должны констатировать, что в вопросах гидродинамики в случае жидкости и аэродинамики в случае газа мы относительно немного продвинулись в понимании природы этих вечно меняющихся течений.
Современному человеку для понимания в деталях характера процессов, происходящих в природе, для планирования жизни надо знать, как распространяются воздушные потоки, как протекает жидкость, как происходит осаждение пыли, очистка газов и пр. Большинство стандартных методов исследования жидкостных или газовых потоков основано на моделировании полей. Поэтому в настоящее время представляет значительный интерес изучение и моделирование скалярных и векторных полей, имеющих место в потоке жидкости или газа. При этом необходима визуализация распределения жидкости и газа, которая позволяет лучше представить, что происходит.
Исследование полей, возникающих в жидкостях и газах, представляет также огромный интерес для промышленности, в частности для химической технологии, так как подавляющее число процессов в химической промышленности основано на течении жидкофазной или газофазной смеси реагентов через различные среды.
Понимание структуры полей жидкостей и газов важно при создании технических средств пожаротушения для того, чтобы создавать наилучшие способы подачи огнетушащего вещества (воды или водяных растворов поверхностно активных веществ) в очаг пожара, на охлаждаемую поверхность или в защищаемую зону, чтобы создавать водяные завесы, полученные путем использования специального противопожарного оборудования.
При анализе процесса переноса субстанций (газов, жидкостей и пр.) различают конвективный (или молярный) и диффузионный (или молекулярный) перенос.
Конвективный перенос физической
субстанции связан с движением сплошной
среды, определяемым векторным полем ее
скорости
![]() в момент времени
.
Интенсивность переноса физической
субстанции определяется плотностью
потока, равной количеству субстанции,
переносимой в единицу времени через
единичную площадку, перпендикулярную
направлению переноса. Для физической
субстанции, выражаемой скалярной
величиной, плотность потока конвективного
переноса является вектором, коллинеарным
вектору скорости
и равным произведению
и объемной плотности этой субстанции.
Так направление и интенсивность
конвективного переноса массы газа или
жидкости определяет вектор плотности
потока массы
в момент времени
.
Интенсивность переноса физической
субстанции определяется плотностью
потока, равной количеству субстанции,
переносимой в единицу времени через
единичную площадку, перпендикулярную
направлению переноса. Для физической
субстанции, выражаемой скалярной
величиной, плотность потока конвективного
переноса является вектором, коллинеарным
вектору скорости
и равным произведению
и объемной плотности этой субстанции.
Так направление и интенсивность
конвективного переноса массы газа или
жидкости определяет вектор плотности
потока массы
![]() .
.
Диффузионный перенос физических
субстанций может происходить и при
отсутствии направленного движения
среды (например, при хаотическом
молекулярном движении в жидкости, газе).
При неравномерном пространственном
распределении в среде некоторой
физической субстанции объемной плотностью
![]() хаотическое движение микрочастиц среды
постепенно приводит к выравниванию
этого распределения.
хаотическое движение микрочастиц среды
постепенно приводит к выравниванию
этого распределения.
В изотропной среде, свойства которой
одинаковы во всех направлениях,
диффузионный перенос физической
субстанции, вызванный неравномерным
пространственным распределением
скалярной величины
,
происходит в направлении убывания
объемной плотности, то есть в направлении,
противоположном направлению градиента
![]() скалярного поля, заданного в пространстве
в текущий момент времени
функцией
скалярного поля, заданного в пространстве
в текущий момент времени
функцией
![]() .
.
Как известно, ключевыми параметрами для описания течения жидкостей и газов в среде являются величины скоростей потока.
Атмосфера – это сильно подвижная физическая субстанция, в которой всегда происходит различные по масштабам, направлениям и скорости движения.
Эти движения в редких случаях могут быть ламинарными. Ламинарными называют такие движения, при которых частички атмосферы имеют плавные траектории, которые распределяются параллельно одна другой. В этом случае взаимодействие между отдельными частичками потока происходит только благодаря тепловому движению молекул.
Напротив, намного чаще движения в атмосфере есть турбулентными. Турбулентным называют движение субстанции, характеристики которого упорядоченно сменяются в пространстве и во времени при неизменных внешних условиях. При таком движении возникают вихри различных размеров. В турбулентных потоках можно выделить элементарные массы воздуха, которые возникнув, отрываются от общего потока, некоторое время двигаются самостоятельно, потом распадаются или смешиваются с общим потоком воздуха. Все это приводит до интенсивного перемешивания между разными частицами среды и к сильному их взаимодействию.
О характере движения воздуха в атмосфере свидетельствует форма распространения дыма, который выходит из трубы. При малых скоростях ветра (отсутствии конвективного движения) дым тонкой струйкой за счет диффузионного и теплового движения поднимается вверх, что свидетельствует о ламинарном движении. При возрастании скорости ветра дым завихряется, его движение становится турбулентным
Опыты, демонстрируемые Вам в школе, показывают, что могут быть разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела.
Посмотрим, как происходит переход ламинарного потока в турбулентный. Откроем кран и пустим воду сначала тоненькой струйкой, а потом все сильнее и сильнее. Тоненькая струйка движется плавно и спокойно. По мере того, как увеличивается напор воды, скорость струи растет, и, начиная с некоторого момента, вода в ней начинает закручиваться - возникают вихри. Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение - оно становится турбулентным.
Рис. 19. Фотография турбулентной струи воды, образующейся в кране
Оценить скорость течения жидкости или газа, при которой возникает турбулентность, можно при помощи так называемого числа Рейнольдса
Re = ρvl/μ,
где ρ - плотность жидкости или газа,
μ - их вязкость (вязкость воздуха, например, 18,5.10-6 Па.с; воды - 8,2.10-2 Па.с),
v - скорость потока, l - характерный линейный размер (диаметр трубы, длина обтекаемого тела и пр.).
Для каждого вида течений существует такая критическая величина Reкр, что при Re<Reкр возможно только ламинарное течение, а при Re>Reкр оно может стать турбулентым.
Если в массе движущейся жидкости взять какую-либо частицу жидкости и проследить ее путь за какой-то промежуток времени (конечный, достаточно большой), то можно получить некоторую линию, выражающую геометрическое место этой точки в пространстве за время.
Если в массе движущейся жидкости в данный момент времени t взять какую-либо точку (рис. 12), то можно в этой точке построить векторы скорости, выражающие мгновенную величину и направление скорости движения частицы жидкости в данной точке в этот момент времени.
Установившимся стационарным движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и гидродинамическое давление р не изменяются с течением времени, т.е. зависят только от координат точки. Неустановившимся (нестационарным) движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и гидродинамическое давление р – постоянно изменяются, то есть зависят не только от положения точки в пространстве, но и от времени.
Примером установившегося движения может быть: движение жидкости в канале, в реке при неизменных глубинах, истечение жидкости из резервуара при постоянном уровне жидкости в нем и др. Неустановившееся движение – это движение жидкости в канале или реке при переменном уровне или при опорожнении резервуара, когда уровень жидкости в нем непрерывно изменяется. Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.
Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются. В этом случае средние скорости по длине потока также не изменяются. Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.
Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и постоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.
Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).
Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное. Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.
Введите в командное окно MATLAB програму 9.
Изучите, какой вид будут иметь картина поля потока воды. Обратите внимание, что для визуализации потоков и жидкостных струй используются маленькие конусы. Вы вероятнее всего еще в детстве по наитию исследовали течение ручейков, пуская по ним маленькие кораблики. Конусы – это нечто подобное при компьютерном моделировании.
Програма 9.
cla
load wind
[cx cy cz] = meshgrid(linspace(71,134,10),linspace(18,59,10),3:4:15);
daspect([1 1 1])
h=coneplot(x,y,z,u,v,w,cx,cy,cz,y,3);
set(h,'EdgeColor', 'none');
colormap(hsv);
box on;
axis tight
camproj perspective;
camva(35);
campos([175 10 85]);
camtarget([105 40 0])
camlight left;
lighting gouraud
На полученном изображении в движущейся жидкости можно взять некоторые точки, в которых также можно построить векторы скоростей, выражающие скорость движения частиц жидкости в один тот же момент. Скорость, направление и отображают конусы. Можно, используя конусы провести через них плавную кривую, к которой векторы скоростей будут всюду касательны. Эта линия и называется линией тока.
Таким образом, линией тока называется линия, проведенная через ряд точек в движущейся жидкости так, что в данный момент времени векторы скорости частиц жидкости, находящихся в этих точках, направлены по касательной к этой линии. В отличие от траектории, которая показывает путь движения одной частицы жидкости за определенный промежуток времени, линия тока соединяет разные частицы и дает некоторую мгновенную характеристику движущейся жидкости в момент времени t. Через заданную точку в данный момент времени можно провести только одну линию тока.
Если в данных точках движущейся жидкости величина и направление скорости и гидродинамическое давление с течением времени не изменяются (такое движение называется установившимся), то и линия тока, и траектория частицы, оказавшейся на ней, совпадают и со временем не изменяются. В этом случае траектории частиц являются и линиями тока.
На основании анализа изображений, получаемых путем визуализации структуры поля скоростей в потоке жидкости, сделайте выводы о следующем.
Имеет ли поле скоростей в потоке жидкости стоки и истоки?
Имеются в картине турбулентность, свидетельствующая о наличии вихрей в потоке жидкости. Сформулируйте, является ли исследуемое поле скоростей в потоке жидкости потенциальным или соленоидальным.
Введите в командное окно MATLAB програму 10.
Изучите, какой вид будут иметь картина визуального представления струи в пространстве.
Програма 10.
[x y z v] = flow;
p = patch(isosurface(x,y,z,v,-3));
isonormals(x,y,z,v,p);
set(p,'facecolor','red','edgecolor','none');
daspect([1 1 1]);
view(3); axis tight; grid on;
camlight;
lighting gouraud;
alpha(.5)
Если в движущейся жидкости выделить весьма малую элементарную площадку, перпендикулярную направлению течения, и по контуру ее провести линии тока, то полученная поверхность называется трубкой тока, а совокупность линий тока, проходящих сплошь через площадку, образует так называемую элементарную струйку (рис.20).

Рис. 20. Фотография элементарной струйки
Элементарная струйка характеризует состояние движения жидкости в данный момент времени t. При установившемся движении элементарная струйка имеет следующие свойства: 1. форма и положение элементарной струйки с течением времени остаются неизменными, так как не изменяются линии тока; 2. приток жидкости в элементарную струйку и отток из нее через боковую поверхность невозможен, так как по контуру элементарной струйки скорости направлены по касательной; 3. скорость и гидродинамическое давление во всех точках поперечного лечения элементарной струйки можно считать одинаковым ввиду малости площади.
Совокупность элементарных струек движущейся жидкости, проходящих через площадку достаточно больших размеров, называется потоком жидкости.
Введите в командное окно MATLAB програму 11.
Изучите, какой вид будут иметь картина визуального представления совокупности элементарных струек движущейся жидкости в пространстве.
Програма 11.
cla
[sx sy sz] = meshgrid(80, [20 30 40], [5 10]);
daspect([1,1,1]);
h=streamtube(x,y,z,u,v,w,sx,sy,sz);
set(h,'facecolor','cyan','edgecolor','none');
box on;
camproj perspective;
axis([70 138 17 60 2.5 16]);
axis tight
camva(28);
campos([175 10 95]);
camtarget([105 40 0])
camlight left;
lighting gouraud
Введите в командное окно MATLAB програму 12.
Изучите, какой вид будут иметь совместная картина визуального представления совокупности элементарных струек и потоков движущейся жидкости с помощью конусов в пространстве.
Програма 12.
cla
spd = sqrt(u.*u + v.*v + w.*w);
p = patch(isosurface(x,y,z,spd, 40));
isonormals(x,y,z,spd, p)
set(p, 'FaceColor', 'red', 'EdgeColor', 'none');
p2 = patch(isocaps(x,y,z,spd, 40));
set(p2, 'FaceColor', 'interp', 'EdgeColor', 'none')
daspect([1 1 1]);
[f verts] = reducepatch(isosurface(x,y,z,spd, 30), .2);
h=coneplot(x,y,z,u,v,w,verts(:,1),verts(:,2),verts(:,3),2);
set(h, 'FaceColor', 'cyan', 'EdgeColor', 'none');
[sx sy sz] = meshgrid(80, 20:10:50, 0:5:15);
h2=streamline(x,y,z,u,v,w,sx,sy,sz);
set(h2, 'Color', [.4 1 .4]);
colormap(jet)
box on
axis tight
camproj perspective;
camva(34);
campos([165 -20 65]);
camtarget([100 40 -5])
camlight left;
lighting gouraud
Введите в командное окно MATLAB програму 13.
Изучите, какой вид будут иметь совместная картина визуального представления развития такого сложного явления как развитие атмосферных вихрей (типа смерча) в пространстве.
Сложные атмосферные явления, такие, как вихри, торнадо и смерчи нередко поднимают не только пыль с земли, но и различные предметы – от камней до автомобилей и деревянных домов.
Програма 13.
load wind;
[sx sy sz]=meshgrid (100,20:2:50,5);
verts=stream3(x,y,z,u,v,w,sx,sy,sz);
s1=streamline(verts);
view(-10.5,18);
daspect([2 2 0.125]);
axis tight;
box on;
iverts=interpstreamspeed(x,y,z,u,v,w,verts,0.05);
set(gca,'drawmode','fast');
streamparticles(iverts,15,'Animate',10,'ParticleAlignment','on' ...
,'MarkerEdgeColor','none','MarkerFaceColor','red','Marker','o');
Введите в командное окно MATLAB програму 14.
Изучите, какой вид будут иметь картина визуального представления развития смерча в ограниченном пространстве.
Програма 14.
load wind;
[sx sy sz]=meshgrid (80,20:1:50,5);
verts=stream3(x,y,z,u,v,w,sx,sy,sz);
s1=streamline(verts);
iverts=interpstreamspeed(x,y,z,u,v,w,verts,0.025);
axis tight;
view(30,30);
daspect([1 1 0.125]);
camproj perspective;
camva(8)
set(gca,'DrawMode','fast');
box on;
streamparticles(iverts,35, ...
'animate',10,'ParticleAlignment','on')
