1. Численные методы решения нелинейных уравнений
Численные методы решения нелинейных уравнений
1-ый этап решения – локализация корней
Реализация 1-го этапа в MS Exсel
2-ой этап - уточнение корня
Метод касательных. Реализация метода
Метод хорд. Реализация метода
Метод половинного деления. Реализация метода
Решение нелинейного уравнения с помощью надстройки «Поиск решения»
1.1 Численные методы решения нелинейных уравнений
Решение некоторых строительных задач сводится к решению достаточно сложных нелинейных уравнений, которые могут представлять собой самостоятельную задачу. Корни таких уравнений сравнительно редко удается найти точными методами. Кроме того, в некоторых случаях и коэффициенты уравнения, полученные в процессе эксперимента или как результаты предварительных расчетов, известны лишь приблизительно. Следовательно, сама задача о точном определении корней уравнения теряет смысл и важное значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.
Нелинейными (трансцендентными) уравнениями называют уравнения, содержащие всевозможные элементарные функции (алгебраические, логарифмические, тригонометрические или показательные).
В общем виде нелинейное уравнение с одним неизвестным можно представить в виде
f (x) = 0, (1.1)
где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале a < x < b .
|
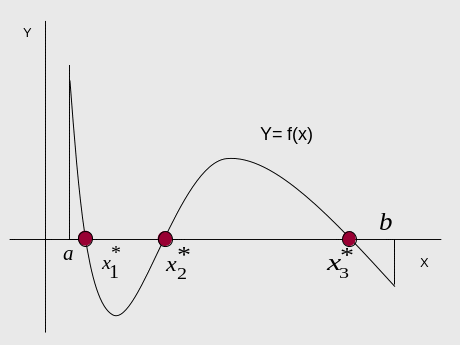
Всякое значение x*, обращающее уравнение y=f(x) в тождество, называется корнем этого уравнения, т.е. f(x*) 0. С геометрической точки зрения задача нахождения корней уравнения эквивалентна задаче нахождения нулей функции у=f(x) или абсцисс точек пересечения графика функции c осью Х, т.е. значений xi , для которых выполняется условие f (xi) = 0 (для i=1, 2,……). Исходя из специфики строительных задач, будем рассматривать только действительные корни уравнения. |
Убедится в том, что на данном отрезке x [a, b] (например, грубо определенном графическим способом) действительно имеется единственный корень уравнения f(x)= 0 , можно аналитическим способом, в основе которого лежит известная теорема1 математического анализа.
Теорема1 |
Если функция у=f(x) удовлетворяет на отрезке [a, b] следующим условиям:
то уравнение f (x) = 0 имеет единственный корень x* на интервале [а, b]. |
Методы решения нелинейных уравнений делятся на 2 группы:
точные (прямые) и
итерационные (приближенные).
Точные методы позволяют записать корни уравнения в аналитическом виде, т.е. в виде некоторой формулы. Однако, многие уравнения не имеют аналитического решения.
Итерационные (приближенные) методы - это методы последовательных приближений, алгоритм которых состоит из двух этапов.
1-ый этап - отделение или локализация корней.
2-ой этап - уточнение приближенного значения корня до заданной точности .
1-ый этап решения – локализация корней
На этом этапе необходимо решить следующие задачи:
исследовать количество и расположение корней;
найти начальное значение корня (нулевая итерация –х0) или выделить из области допустимых значений (ОДЗ) функции f(x) отрезок, на котором существует единственный корень.
Принимая во внимание, что для функции общего вида не существует универсальных методов решения задачи локализации корней, рассмотрим некоторые из этих способов.
1. Строится таблица значений функции у=f(x) на некотором отрезке x [А, В] (табулирование функции). Отыскивается отрезок, на концах которого функция имеет разные знаки, тогда на этом отрезке находится хотя бы один корень уравнения.
2. Графический метод. Принимая во внимание, что действительные корни уравнения f(x)=0 — это абсциссы точек пересечения графика функции y=f(x) с осью Х, достаточно построить график этой функции и отметить точки её пересечения с осью Ох.
3. Убедится в том, что на данном отрезке x [a, b], определенным 1 или 2-ым способом действительно имеется единственный корень уравнения f(x)= 0 , можно аналитическим способом, в основе которого лежит известная теорема1 математического анализа.