3. Релаксационные безызлучательные переходы.

Кроме переходов, связанных с поглощением и излучением квантов электромагнитного поля (фотонов) возможен иной путь изменения энергии системы, при котором избыточная, а иногда – недостающая энергия отдается или принимается в результате тепловых процессов – столкновений с другими атомами/молекулам/ионами или отдается фононам – квантам колебаний кристаллической решетки твердого тела.

4. Ширина и форма спектральной линии.

При первом рассмотрении нами принималось, сто разрешенные уровни энергии в атомах и молекулах являются бесконечно узкими, а процесс излучения кванта не подвержен каким-либо возмущениям. Соответственно, квантовым переходам соответствует бесконечно узкая спектральная линия излучения (поглощения) то есть идеально монохроматическая волна. Это приводит к тому, что при любой конечной интегральной мощности излучения его спектральная плотность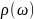 неограниченно возрастает. В реальной ситуации этого не происходит, поскольку существует набор факторов увеличивающий ширину спектральной линии до конечной величины. В этом случае распределение интенсивности излучения по частотам в пределах линии описывается функцией q(ω), называемой форм-фактором линии. Нормировка форм-фактора производится из условия

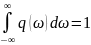
1. Естественное уширение спектральной линии.

Естественное уширение спектральной линии фундаментально, то есть присутствует всегда и избавиться от него невозможно. Оно связано с конечностью времени жизни системы в возбужденном состоянии. Вытекает из соотношения неопределенностей Гейзенберга и имеет вид узкого Лоренцевского контура:

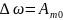
Если есть возможность спонтанного перехода на несколько нижних уровней, то ширина линии численно равна сумме коэффициентов Эйнштейна для переходов на эти уровни:

Расчет формы естественно-уширенной линии в приближении квантовой электродинамики и в модели классического осциллятора показывают абсолютно одинаковый результат. Чем меньше время жизни в возбужденном состоянии, т.е. чем больше вероятность спонтанного перехода, тем больше уширение линии.

Типовое значение естественной ширины линии для видимой области составляет 20 МГц при основной частотеν₀=5*10¹⁴Гц для рарешенных переходов и 200-1000 Гц для запрещенных переходов. В случае аммиачного мазера ν₀=24870 МГц ширина линии составляет 10^-3 Гц.

4.2 Доплеровское уширение.

Как следует из названия, в основе лежит эффект Доплера, заключающийся при взаимном сближении или удалении источника и приемника излучения. В случае их сближения воспринимаемая приемником частота сигнала возрастает, в случае удаления – падает. В общем виде выражение для изменения частоты записывается в следующем виде:

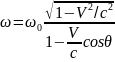
Для случая малых скоростей данное выражение может быть записано как

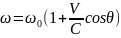
Скорость считается положительной при взаимном сближении источника и приемника.

В случае теплового движения мы имеем хаотическое движение атомов или молекул, являющимися как приемниками, так и источниками излучения. При этом происходит сдвиг резонансной линии каждой микрочастицы, причем индивидуально, в зависимости от скорости и направления движения.

Вследствие большого количества таких частиц в системе происходит статистическое усреднение, в результате которого мы получаем уширенный контур как бы «набитый» линиями отдельных атомов (молекул). Статистика различных частот в пределах контура соответствует тепловому распределению по направлениям и скоростям движения. В соответствии с вышесказанным характерная ширина доплеровски уширенного контура определяется наиболее вероятной скоростью частиц в ансамбле, т.е. его температурой.

Распределение частиц по скоростям описывается кривой Максвелла:

При этом

В этом случае форма контура описывается функцией

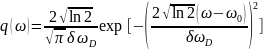
сводящейся к Гауссовому распределению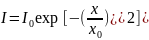

А доплеровская полуширина контура

При этом

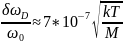
Оценим уширение для условий газового разряда в легком газе:

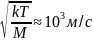
В видимой области Гц Доплеровская ширина контура ГГц.

Для аммиачного мазера 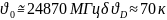Гц, т.е. Доплеровское уширение в миллионы раз превышает естественное уширение.