2. Теорема сложения вероятностей.

Рассмотрим теоремы, позволяющие вычислить вероятность появления события А или В в результате одного испытания, т.е. вероятность суммы этих событий А+В. Возможны два случая: события совместны и несовместны.

 Теорема1: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).

Доказательство:

Число всех исходов N, число исходов благоприятствующих событию  А- К, событию В- L. Так как А и В несовместны, то ни  один из этих исходов не может благоприятствовать А и В одновременно, т.е. А и В взаимно исключающие, следовательно число благоприятствующих исходов для события А+В равно К+L. Тогда вероятность равна

  

 Теорема2: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ).

Доказательство:

Всего исходов N, благоприятствующих событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L-M. Откуда вероятность события А+В:

Решим задачи:

Пример1. Найти вероятность суммы противоположных событий.

Решение: События А и А  несовместны, следовательно Р( А +А ) = Р(А) + Р( А). Сумма двух противоположных событий есть событие достоверное, поэтому Р( А +А )= 1. Тогда Р(А) + Р( А ) =1. Отсюда следует :

Р( А) = 1 - Р(А).

Пример2. В урне 3 красных, 5 синих и 2 белых шара. Наудачу вынимают один шар. Какова вероятность того, что шар окажется цветным?

Решение:

Пусть событие А- вынут синий шар, событие В- красный шар. Эти события несовместны. Интересующее событие- вынут цветной шар, означает, что вынут красный или синий, т.е. событие А+В. используем теорему о сумме несовместных событий Р(А+В)=Р(А)+Р(В). вычислим вероятности событий А и В:

Р(А)=5/10=1/2;   Р(В)=3/10.  Тогда искомая вероятность равна Р(А+В) = 1/2+3/10= 8/10=0,8.

Пример3. В посевах пшеницы на поле 95% здоровых растений. Берут любые два растения. Найти вероятность того, что хотя бы одно из них здоровое.

Решение:

Пусть событие- здорово первое растение - А, здорово второе растение - В. Тогда событие- здорово хотя бы одно из них, т. е. А или В-  А+В. События А и В совместны, следовательно применим  теорему о сумме двух совместных событий Р(А+В)= Р(А)+Р(В)-Р(АВ). Вероятность того, что растение здорово равна 0,95 и одинакова для обоих растений. Вероятность Р(АВ) вычислим по теореме о произведении двух независимых событий, т.е. Р(АВ)=Р(А)Р(В). получим:

Пример4. По мишени стреляют три стрелка. Вероятности попадания соответственно равны 0,7; 0,8 и 0,9. Найти вероятность того, что  попадут какие – либо два стрелка.

Решение: Пусть события А- попал 1-ый стрелок, В – попал 2- ой, С – попал 3- ий. События независимые . Событие  D– попадут только два стрелка выразим через А, В и С: 

  

 Применяя теоремы умножения независимых событий и сложения несовместных событий получим:

   

3. Вероятность наступления хотя бы одного из нескольких попарно независимых событий.

 При решении некоторых задач событие, вероятность которого необходимо найти, приходится представлять в виде суммы нескольких событий. Это представление может быть громоздким. В этом случае имеет смысл воспользоваться вычислением вероятности противоположного события. Рассмотрим пример.

Три станка работают независимо. Вероятность поломки каждого из них соответственно равна 0,1; 0,2; 0,3. Найти вероятность того, что хотя бы один станок выйдет из строя.

Пусть событие- поломка 1-го станка -А; поломка 2-го- В, поломка 3-го- С. Тогда событие D - поломка хотя бы одного (одного или двух, или трех) запишется следующим образом:

     

Вычислять вероятность  по полученному представлению неудобно из-за большого количества вычислений. Составим противоположное событие событию D. Итак , D - исправны все три станка. Это событие представим в виде произведения- А В С.

Применим теорему  о произведении независимых событий, тогда:

Вероятность события D будет равна:

Обобщим результаты задачи в виде теоремы:

 Вероятность появления хотя бы одного из событий А₁, А₂,…,А_n независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий, т.е.

  Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу   о том, что эта случайная величина подчиняется закону распределения  . Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение  исследуемой случайной величины. Сравнение эмпирического распределения   и теоретического (или, точнее было бы сказать, гипотетического — то есть соответствующего гипотезе  ) распределения   производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Содержание   [убрать]  1 Статистика критерия 2 Правило критерия 3 Литература 4 См. также 5 Ссылки

[править]Статистика критерия

Для проверки критерия вводится статистика:

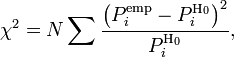
где   — предполагаемая вероятность попадания в  -й интервал,   — соответствующее эмпирическое значение,   — число элементов выборки из  -го интервала,   — полный объём выборки. Также используется расчет критерия по частоте, тогда:

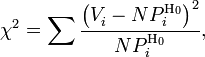
где   — частота попадания значений в интервал. Эта величина, в свою очередь, является случайной (в силу случайности  ) и должна подчиняться распределению  .

[править]Правило критерия

Перед тем как сформулировать правило принятия или отвержения гипотезы, необходимо учесть, что критерий Пирсона обладает правосторонней критической областью.

Правило. Если полученная статистика превосходит квантиль закона распределения   заданного уровня значимости   с   или с   степенями свободы, где   — число наблюдений или число интервалов (для случаяинтервального вариационного ряда), а   — число оцениваемых параметров закона распределения, то гипотеза  отвергается. В противном случае гипотеза принимается на заданном уровне значимости  .

U-критерий Манна — Уитни (англ. Mann — Whitney U-test) — статистический критерий, используемый для оценки различий между двумя независимыми выборками по уровню какого-либо признака, измеренного количественно. Позволяет выявлять различия в значении параметра между малыми выборками.

Другие названия: критерий Манна — Уитни — Уилкоксона (англ. Mann — Whitney — Wilcoxon, MWW), критерий суммы рангов Уилкоксона (англ. Wilcoxon rank-sum test) или критерий Уилкоксона — Манна — Уитни (англ. Wilcoxon — Mann — Whitney test). Реже: критерий числа инверсий^[1].

Содержание   [убрать]  1 История 2 Описание критерия 3 Ограничения применимости критерия 4 Использование критерия 5 Таблица критических значений 6 См. также 7 Примечания 8 Литература

[править]История

Данный метод выявления различий между выборками был предложен в 1945 году Фрэнком Уилкоксоном (F. Wilcoxon). В 1947 году он был существенно переработан и расширен Х. Б. Манном (H. B. Mann) и Д. Р. Уитни (D. R. Whitney), по именам которых сегодня обычно и называется.

[править]Описание критерия

Простой непараметрический критерий. Мощность критерия выше, чем у Q-критерия Розенбаума.

Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.

[править]Ограничения применимости критерия

1. В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было два значения, но во второй тогда не менее пяти.

2. В выборочных данных не должно быть совпадающих значений (все числа — разные) или таких совпадений должно быть очень мало.

[править]Использование критерия

Для применения U-критерия Манна — Уитни нужно произвести следующие операции.

1. Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным:

где   — количество единиц в первой выборке, а   — количество единиц во второй выборке.

2. Разделить единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок. Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определить большую из двух ранговых сумм ( 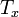), соответствующую выборке с 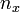  единиц.

3. Определить значение U-критерия Манна — Уитни по формуле:

4. По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных и . Если полученное значение  меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение  больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение .

5. При справедливости нулевой гипотезы критерий имеет математическое ожидание  и дисперсию  и при достаточно большом объёме выборочных данных распределён практически нормально.

[править]

F-тестом или критерием Фишера (F-критерием, φ*-критерием) — называют любой статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение).

Статистика теста так или иначе сводится к отношению выборочных дисперсий (сумм квадратов, деленных на "степени свободы"). Чтобы статистика имела распределение Фишера необходимо, чтобы числитель и знаменатель были независимыми случайными величинами и соответствующие суммы квадратов имели распределение Хи-квадрат. Для этого требуется, чтобы данные имели нормальное распределение. Кроме того, предполагается, что дисперсия случайных величин, квадраты которых суммируются, одинакова.

Тест проводится путем сравнения значения статистики с критическим значением соответствующего распределения Фишера при заданном уровне значимости. Известно, что если , то . Кроме того, квантили распределения Фишера обладают свойством . Поэтому обычно на практике в числителе участвует потенциально большая величина, в знаменателе - меньшая и сравнение осуществляется с "правой" квантилью распределения. Тем не менее тест может быть и двусторонним и односторонним. В первом случае при уровне значимости   используется квантиль , а при одностороннем тесте  ^[1].

Более удобный способ проверки гипотез - с помощью p-значения  - вероятностью того, что случайная величина с данным распределением Фишера превысит данное значение статистики. Если  (для двустороннего теста - )) меньше уровня значимости , то нулевая гипотеза отвергается, в противном случае принимается.

Содержание   [убрать]  1 Примеры F-тестов 1.1 F-тест на равенство дисперсий 1.1.1 Две выборки 1.1.2 Несколько выборок 1.2 Проверка ограничений на параметры регрессии 1.2.1 Замечание 1.3 Проверка значимости линейной регрессии 1.3.1 Пример 1.4 Проверка гетероскедастичности 2 См. также 3 Примечания 4 Внешние ссылки