1.4. Деформації

1.4.1. Що таке деформація тіла?

Деформація пов'язана зі зміною взаємного положення окремих точок тіла, яка призводить до зміни форми та розмірів тіла без зміни його маси. Розглядають переміщення і два види деформацій: лінійна деформація та кутова або зсув. Переміщення - це зміна положення координат точки тіла при його деформації. Переміщення позначається и, v, w по відповідних осях координат х, у, z. Лінійна деформація по відповідних осях визначається через переміщення, як:

Кутова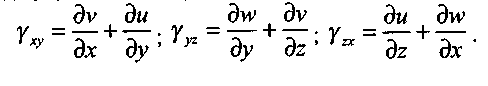 деформація або зсув також визначається через переміщення:

1.4.2. Що таке деформований стан?

• Деформований стан визначається сукупністю деформацій лінійних елементів, спрямованих відповідними осями, які виходять з точки тіла. Отже, деформований стан характеризується трьома лінійними дефор­маціямита трьома кутовими деформаціями(тому що

'. Як і у випадку напружень, загальну картину

деформацій в точці можливо подати у вигляді тензора деформацій:

Якщо за напрямом трьох координатних осей має місце тільки лінійна деформація, а зсув відсутній, то тоді ці осі звуться головними і відповідна лінійна деформація позначається як У випадку, коли

то має місце лінійний деформований стан, при буде плоский деформований стан, а при тіло

знаходиться у об'ємному деформованому стані. Тензори деформац для цих видів деформованого стану ідентичні тензорам відповідного напруженого стану.

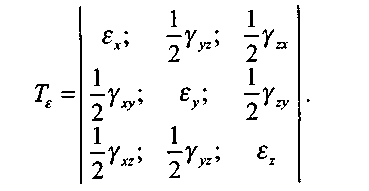
1.5. Напружено-деформований стан

1.5.1. Які існують пружні характеристики матеріалів?

Розрізняють такі пружні характеристики матеріалів: Е - модуль пружності при розтягу, G - модуль пружності при зсуві, [і - коефіцієнт поперечної деформації (коефіцієнт Пуассона). Е і G мають розмірність напружень, - безрозмірний коефіцієнт. Ці постійні характеристики пов'язані між собою залежністю:

Для кожного матеріалу пружні характеристики визначаються експери­ментальним шляхом.

1.5.2. Що собою являє напружено-деформований стан?

Напружено-деформований стан - це сукупність напружень і дефор­мацій в локальному об'ємі (точці) тіла. Залежність між ними в межах теорії пружності визначається законом Гука через пружні характеристики матеріалу, а саме:

- для лінійних деформацій:

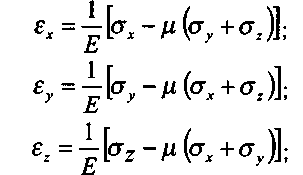
- для кутових дефоимашй:

- для нормальних напружень:

- для дотичних напружень:

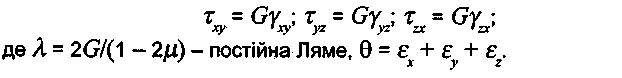
1.6. Геометричні характеристики плоских перерізів

1.6.1. Які основні геометричні характеристики плоских перерізів?

Основними геометричними характеристиками плоских перерізів є:

• статичний момент плоского перерізу відносно осі, що знаходиться в її площині;

• координати центра ваги плоского перерізу;

• моменти інерції плоского перерізу (осьові, полярні);

• радіус інерції плоского перерізу;

• моменти опору плоского перерізу (осьові, полярні).

1.6.2. Що називається статичним моментом плоского перерізу?

Вирази називаються статичними моментами

F F

плоского перерізу відносно осей (рис. 1.5), де z, у - відстань від

центра ваги перерізу відповідно до осі - площа перерізу.

Рис. 1.5. Визначення геометричних характеристик

Якщо площа перерізу має просту форму і положення центра ваги визначене то статичнімоменти визначаються за формулами:

Д ля складної форми перерізу статичний момент визначається як сума статичних моментів складових перерізів простої форми, для яких положення центру ваги відоме, а саме:

де/- площа г'-ої частини перерізу. Статичний момент відносно осей, що проходять через центр ваги (центральні осі), дорівнює нулю.

1.6.3. Як визначається положення центра ваги перерізу?

Координати центра ваги перерізу відносно обраних осей у і z визна­чаються:

де/ - площа і-о'і частини перерізу; у. і z. - координати центру ваги.

1.6.4. Що називається осьовим моментом інерції плоского перерізу?

Осьовими моментами інерції плоского перерізу називаються такі вирази:

Відносно центральних осей (начало координат с в центрі ваги пере­різу) осьові моменти визначаються, як:

При паралельному переносі осей координат:

де а і b - відстань між осями у і у_с; z і z_c.

1.6.5. Як визначається момент інерції плоского перерізу складної форми?

Момент інерції перерізу складної форми визначається як сума моментів інерції фігур простої форми відповідно до обраної осі:

обраної осі:

1.6.6. Що таке полярний момент інерції плоского перерізу?

Полярним моментом інерції плоского перерізу є вираз: .

де р - відстань від початку координатдо центра ваги перерізу

1.6.7. Який зв'язок між осьовими і полярним моментами інерції?

Осьові і полярний моменти інерції пов'язані залежністю:

1.6.8. Як визначаються радіуси інерції перерізу?

Радіуси інерції перерізу відносно осей у і z визначаються формулами:

1.6.9. Що собою являє момент опору плоского перерізу?

Моментом опору плоского перерізу відносно даної осі є відношення моменту інерції, взятого відносно цієї осі, до відстані від осі до найбільш віддаленого волокна перерізу. Тобто:

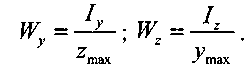
1.6.10. Як визначається полярний момент опору плоского перерізу?

Полярним моментом опору плоского перерізу є сума: