2. Бинарное отношение

Важную роль в анализе различных связей между объектами, изучаемыми гуманитарными науками играет понятие «бинарное отношение».

ПРИМЕР 1

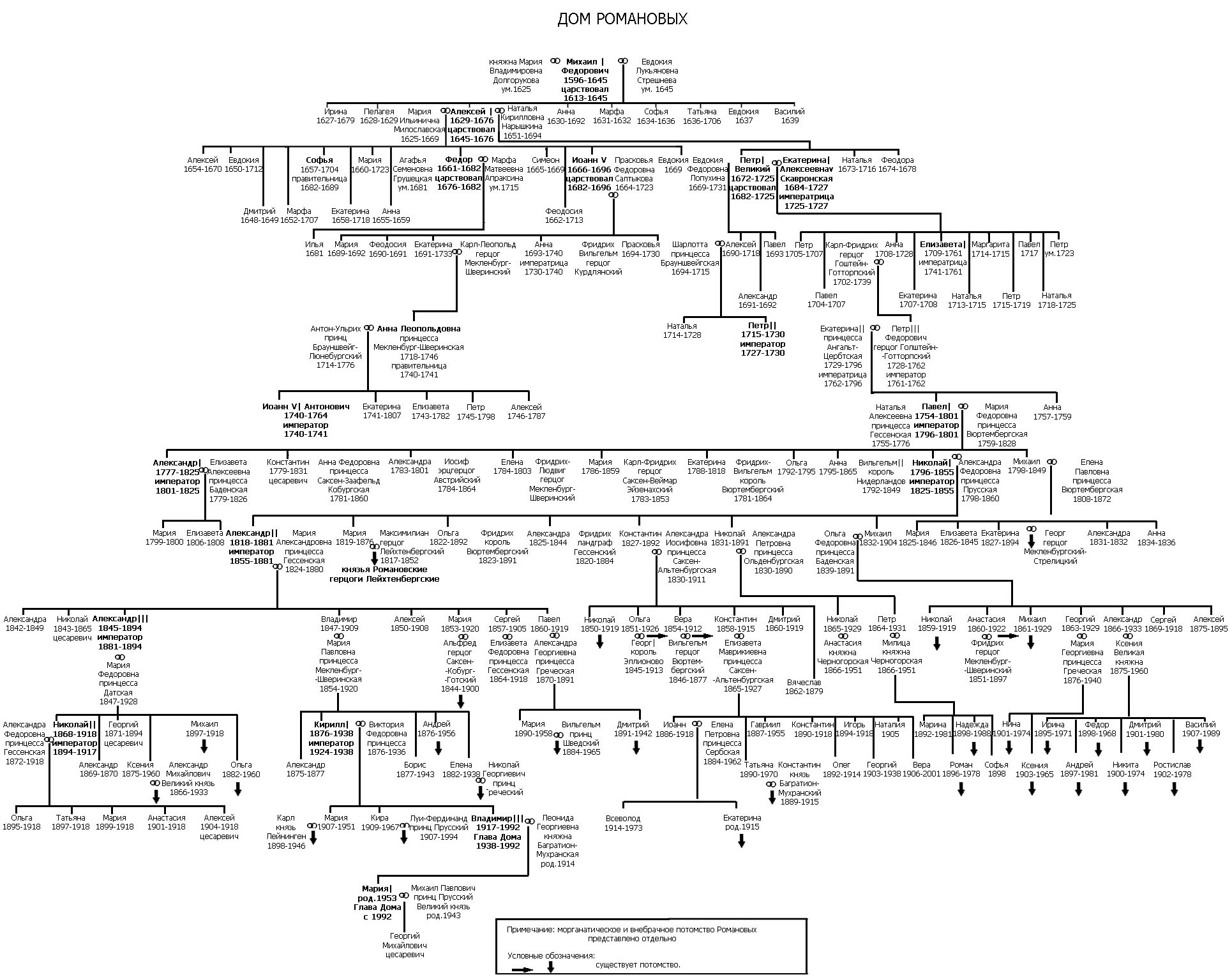
В истории часто используются так называемые генеалогические древа.

Р ис. 1 Древо семьи Павла I

Генеалогическое древо построено на бинарном отношении «Предок-потомок».

ПРИМЕР 2

Формализуем понятие бинарного отношения.

Декартово или прямое произведение:

A X B = {(a,b)|a A  b B}

Говоря простым языком, декартово произведение множеств - это множество всевозможных упорядоченных пар, в которых первый элемент взят из первого множества, а второй – из второго.

Самым известным примером такого произведения является изучаемая в школе координатная плоскость с декартовыми координатами.

Для множеств малой мощности удобным способом наглядного изображения декартова произведение и его подмножеств является таблица (в математике она называется матрицей).

Частным случаем декартова произведения является декартов квадрат

A X A = {(a,b)|a A  b A}

Бинарным отношением на множестве A называется подмножество R декартова квадрата A X A (т. е. подмножество множества всех упорядоченных пар элементов из A). В пределах этого текста xRy будет означать, что (x,y)R.

Для наглядного представления отношений используются таблицы (матрицы). Каждый элемент таблицы соответствует упорядоченной паре элементов из A. Элементы таблицы равны 0 или 1, в зависимости от того, входит ли соответствующая пара в отношение(1) или нет (0).

Пример

А={1,2,3} А состоит из натуральных чисел от 1 до 3.

Таблица его декартова квадрата A² соответствует парам чисел

	1	2	3
1	(1,1)	(1,2)	(1,3)
2	(2,1)	(2,2)	(2,3)
3	(3,1)	(3,2)	(3,3)

Обратите внимание, что, в отличие от привычных из школьного курса декартовых координат на плоскости, первая координата соответствует строкам таблицы, то есть изменяется по вертикали.

О тношение R₁ – строго меньше

	1	2	3
1	0	1	1
2	0	0	1
3	0	0	0

О тношение R₂ – равно

	1	2	3
1	1	0	0
2	0	1	0
3	0	0	1

3. Элементы теории графов

Графом называется бинарное (2-арное) отношение на множестве элементов, называемых вершинами графа. Вершины соединяются дугой (изображается на рисунках стрелкой), если соответствующая упорядоченная пара входит в отношение. Обратите внимание, что исходящая вершина (из которой стрелка выходит) является первой в паре.

Граф называется неориентированным, если стрелки-дуги не имеют направления. В этом случае дуги называются ребрами графа.

Граф называется ориентированным, если все его дуги ориентированы (т.е. имеют исходящую и входящую вершины).

Из определения графа как отношения непосредственно следует естественный способ описания графа в виде матрицы (таблицы) смежности. (Таблица есть отношение.) Матрица квадратная, т.е. числа строк и столбцов совпадают. 1 означает наличие отношения, 0 – отсутствие. Обратите внимание, что номер исходящей вершины

Графы применяются для наглядного изображения бинарных отношений. Этот способ удобен человеку для восприятия таких отношений. Компьютеры же «предпочитают» табличный способ описания отношений. Поэтому мы здесь описываем оба эти способа.

Оба способа дают компактное и наглядное представление об отношениях рассматриваемых элементов (вершин). Многие отчетные данные педагога просят представлять в виде графов. Графы также являются эффективным приемом обеспечения наглядности представления информации в учебном процессе. Владение этими средствами наглядности и программными инструментами, облегчающими их построение — важная компонента компетентности современного учителя.

Пример.

Отношение R – строго меньше на множестве 3 первых натуральных чисел.

Матрица смежности:

	1	2	3
1	0	1	1
2	0	0	1
3	0	0	0

Г раф:

Для наглядности дуги графа помечены теми же цветами, что и соответствующие им элементы матрицы.