
Теория множеств
1. Определение множества и элементарные операции над множествами
Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в информатике.
Мы часто говорим о стае птиц, наборе фломастеров, коллекции минералов, собрании картин и т.д. Обобщая, можно сказать, что речь идет о множестве некоторых предметов. Термин множество широко применяется в математике. Предметы, входящие в рассматриваемое множество, называются его элементами. Кроме основного термина множество, в математике иногда используются его синонимы: система, семейство, класс и др. Однако эти синонимы используются лишь в целях разнообразия языка, и каждый из них может быть заменен универсальным термином «множество».
Множество является первоначальным, базовым математическим понятием, т.е. никакого определения понятия «множество» не предусматривается. А обращение к общеязыковым словам: стая, набор, коллекция, собрание — это не определение, а лишь пояснение смысла этого понятия. Однако есть одно непременное требование к математическому понятию множество: о каждом предмете, каждом элементе должно быть возможно точное выяснение того, принадлежит ли он рассматриваемому множеству или нет.
Обозначим, например, через F множество всех цифр, используемых при десятичной записи чисел. Тогда 5 есть элемент этого множества, 8 тоже его элемент, а 12 и -1 не являются элементами множества F. Но, скажем, множество всех молекул воды, налитой в стакан, не является математически точно определенным вследствие непрерывно происходящих процессов испарения и конденсации.
Пояснения используемых символов:
-символ принадлежности элемента (стоит слева) множеству (стоит справа)
Ø — обозначение пустого множества, не содержащего ни одного элемента.
:= по определению равно
логическое отрицание
логическое «И»
логическое «ИЛИ»
логическое следование (если … то …)
-сокращенно «для всех»
{…} – описание множества
Например:
{1,3,5,8} – описание множества путем перечисления его элементов
{x|логическое выражение-условие} - описание множества путем задания условия, которому должны удовлетворять элементы.
Сравнение множеств
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент B:
A B := { x| x A x B}.
В этом случае A называется подмножеством B, B — надмножеством A. Если A B и (A = B), то A называется собственным подмножеством B. Заметим, что M M M.
Операции над множествами
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями. В результате операций из исходных множеств получаются новые множества.
Два множества называются равными, если они являются подмножествами друг друга: A = B := (A B) (B A)
Операции над множествами
Ниже перечислены основные операции над множествами:
пересечение |
A B := {x|x A x B} |
объединение |
A B := {x|x A x B} |
дополнение |
A_ := {x|(x A)} |
разность |
A \ B := {x|x A (x В)} |
Операция дополнения подразумевает некоторый универсум (множество U, которое содержит A):
A _ :=U \ A
Пример (один из вариантов практического задания на зачете):
А = {2, 3, 4, 7}
B = {3, 4, 5}
A B = {3, 4}
A B = {2, 3, 4, 5, 7}
A \ B = {2,7}
Для лучшего понимания наглядного смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек. Например:
|
|
Диаграмма, иллюстрирующая операцию A B |
Диаграмма, иллюстрирующая операцию A B |
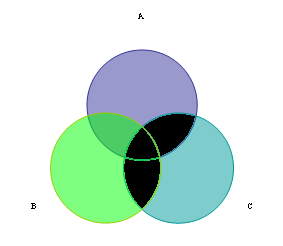
В тесте вам будут встречаться задачи такого типа:
Выбрать формулу, описывающую множество, выделенное на рисунке черным цветом.
В данном случае эта задача решается так:
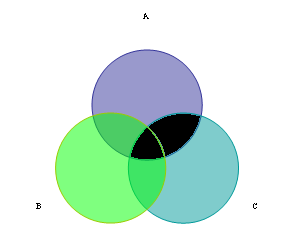
Это – множество А С
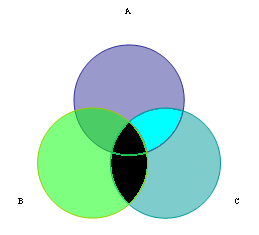
Это – множество C В
Объединение этих двух множеств (C В) (А С) даст нам искомое множество.


