2. Цепи синусоидального тока
2.1. Сведения из теории
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону:
(2.1)
где -
максимальное значение или амплитуда
тока;
- угловая частота;
- фаза;
- начальная фаза.
Угловая частота
,
частота
и период
связаны соотношением:
.
(2.2)
По выражению (2.1)
на рис. 2.1-а построен график функции
,
а на рис.2.1,6 - соответствующая векторная
диаграмма.
Проекция вращающегося
против часовой стрелки с постоянной
угловой скоростью
вектора
(см.рис.2.1,6) на вертикальную ось изменяется
во времени по синусоидальному закону.
Поэтому любая синусоидальная функция
(ток, напряжение, ЭДС) может быть изображена
вектором. На рис.2.1,в изображен вектор
тока с проекциями
и
.
При проведении
расчетов очень удобным оказывается
рассмотрение вращающегося вектора
на комплексной плоскости. В этом случае
вектор
можно представить как комплексную
амплитуду тока
,
а сам синусоидально изменяющийся ток
как мнимую часть произведения комплексной
амплитуды на
тогда при t=0 можно записать:
(2.3)
На практике широкое распространение получил символический метод расчета цепей синусоидального тока.
Сущность
символического (комплексного) метода
состоит в том, что при синусоидальном
токе можно перейти от дифференциальных
уравнений, составленных для мгновенных
значений, к алгебраическим, составленным
относительно комплексов амплитудных
значений тока
,
напряжения
,
ЭДС
либо их действующих значений
и
.
Например, если
то комплексное действующее значение напряжения
где
Аналогично осуществляется запись комплексов действующих значений ЭДС и тока. Например, для схемы (рис. 2.2) уравнение для мгновенных значений напряжений, составленное по второму закону Кирхгофа, запишется следующим образом:
или
Переходя к комплексным действующим значениям напряжений, получим:
где - R активное сопротивление цепи;
- комплексное
индуктивное сопротивление цепи;
-комплексное
емкостное сопротивление цепи.
Множитель
свидетельствует о том, что вектор
напряжения
на индуктивности
опережает вектор тока
на
.
Множитель
показывает, что вектор напряжения
на емкости C
отстает от вектора тока
на
.
На активном сопротивлении
векторы напряжения
и тока
совпадают по направлению.
Величина
называется комплексным сопротивлением
цепи (см. рис. 2.2), а
- её комплексной проводимостью, где
-
активная и реактивная составляющие
проводимости цепи.
Комплексные числа записываются в одной из следующих форм:
алгебраическая -
показательная -
тригонометрическая
-
п
олярная
-
Геометрически
любому комплексному числу
можно поставить в соответствие точку
комплексной плоскости
с координатами x=a,
y=jb
или радиус-вектор длиной
единиц, проведенный из начала координат
в точку
и расположенный под углом
к оси абсцисс (рис. 2.3). Из рисунка очевидны
формулы перехода от одной формы записи
комплексного числа к другой:
Алгебраическая
форма применяется при сложении и
вычитании комплексных чисел, а
показательная - при умножении, делении,
возведении в степень и извлечении корня.
Умножение числа на мнимую единицу
сводится к повороту вектора на угол
против
часовой стрелки, умножение на
- к повороту на угол
по часовой стрелке (рис.2.4), а умножение
на -1 соответствует повороту на
.
Полное комплексное
сопротивление цепи
(см.рис. 2.2) и сопротивления ее участков
(
и
)
геометрически связаны треугольником
сопротивлений (рис.2.5,а,б):
а) если
,
то
б) если
то
Где
;
Р
асчет
электрической цепи в комплексной форме
требует записи одного и того же
комплексного числа в алгебраической и
показательной формах.
Рассмотрим несколько примеров.
Пример 1 иллюстрирован рис.2.6.
=40
Примечания:
1. Аргумент
всех комплексных чисел отсчитывается
от действительной полуоси +1 против
часовой стрелки,
-по часовой стрелке.
2. При вычислении
аргумента
комплексных чисел,
радиус-вектор которых находится во
второй и третьей четвертях комплексной
плоскости, к полученному после операции
числу необходимо прибавить
:
либо из этого числа вычесть :
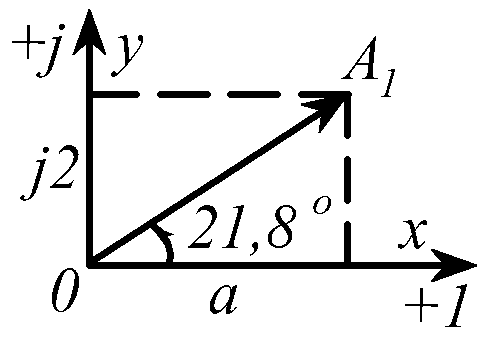
Для расчета электрических цепей переменного тока символическим методом применяются все методы, описанные выше для цепей постоянного тока.
Рис.2.6