1.3. Задачи для самостоятельного решения

1.3.1. Определение входного сопротивления

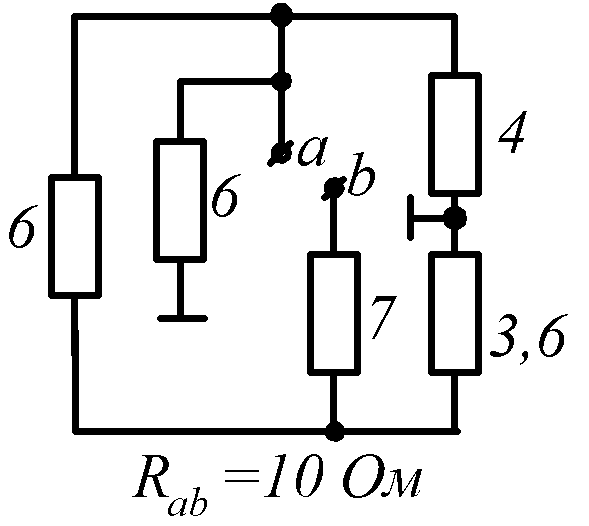
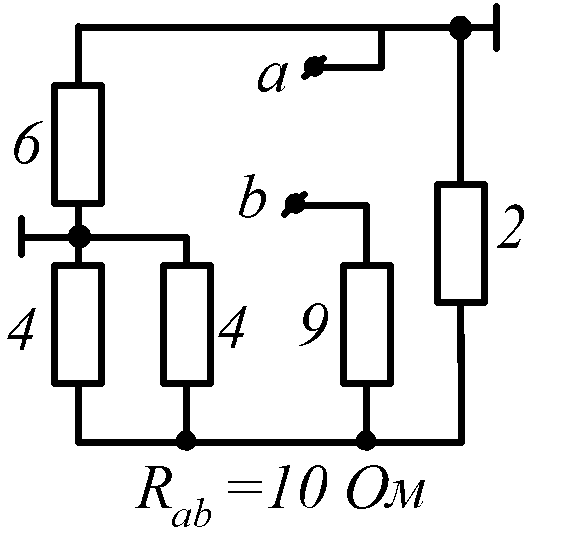
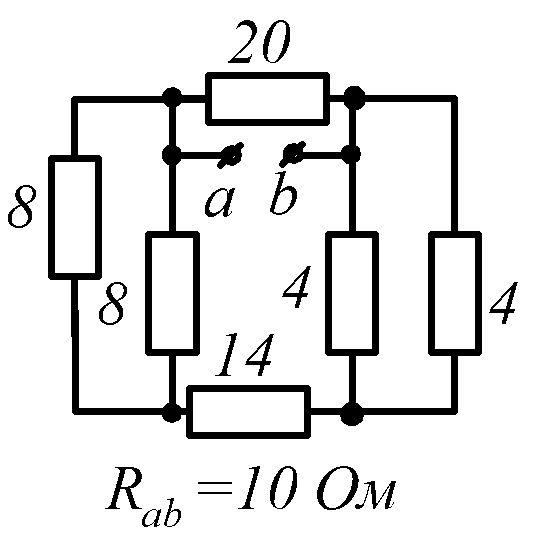
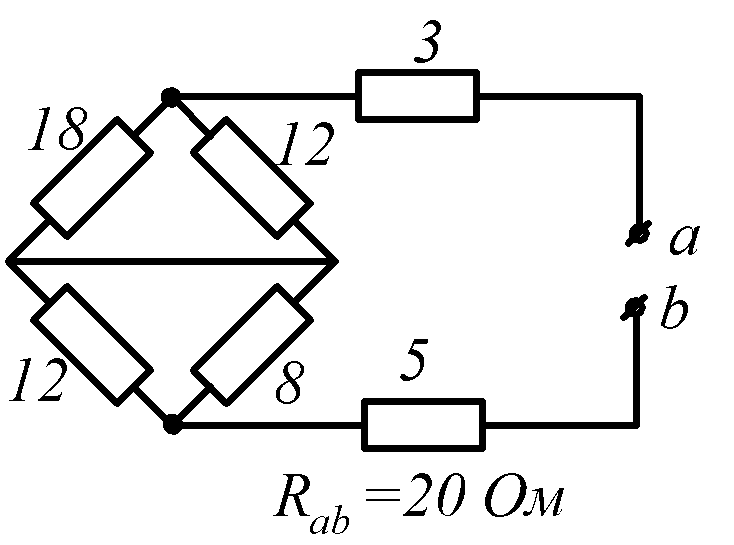
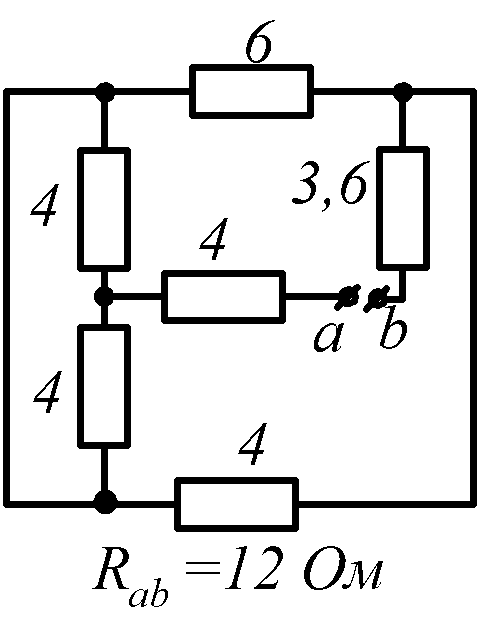
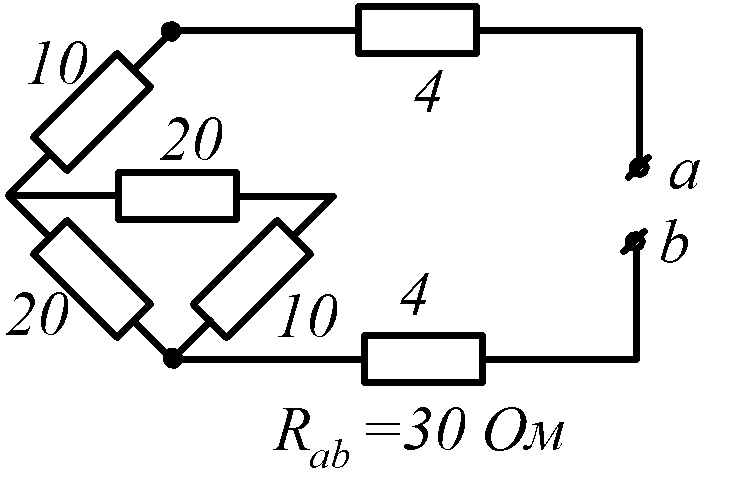
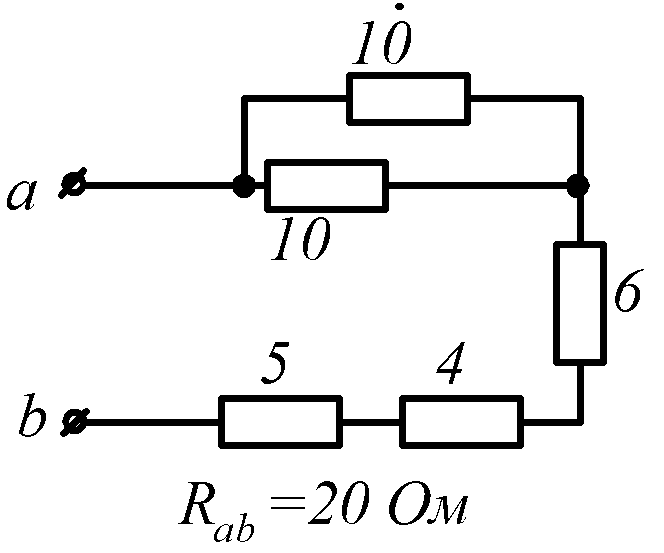
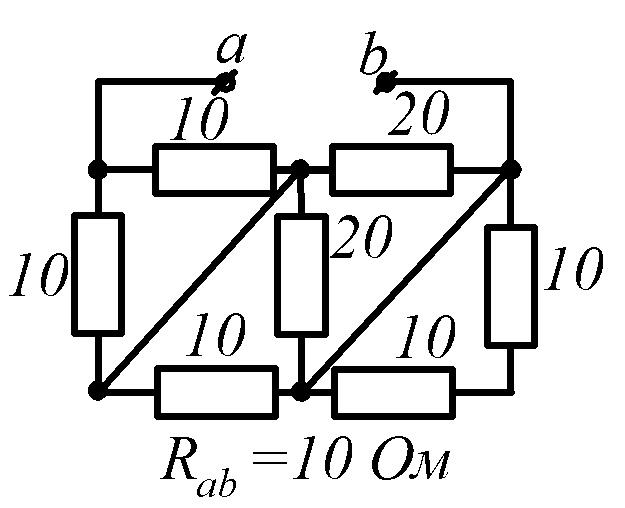
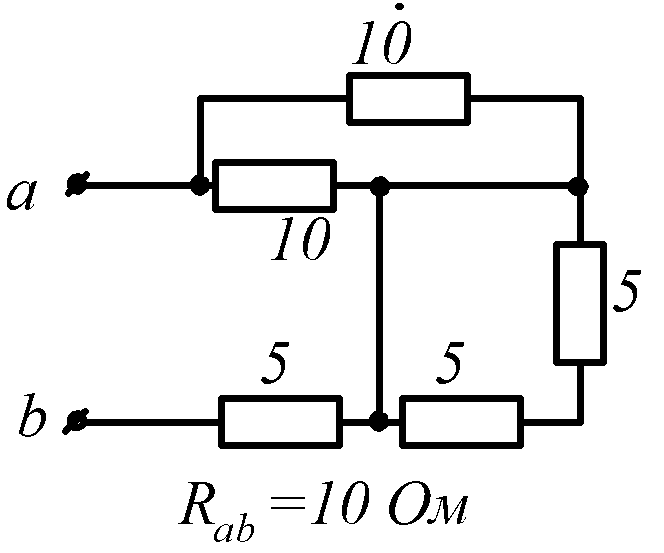
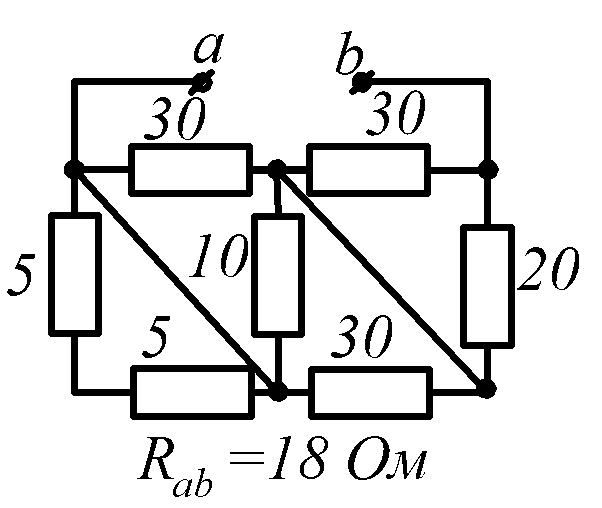
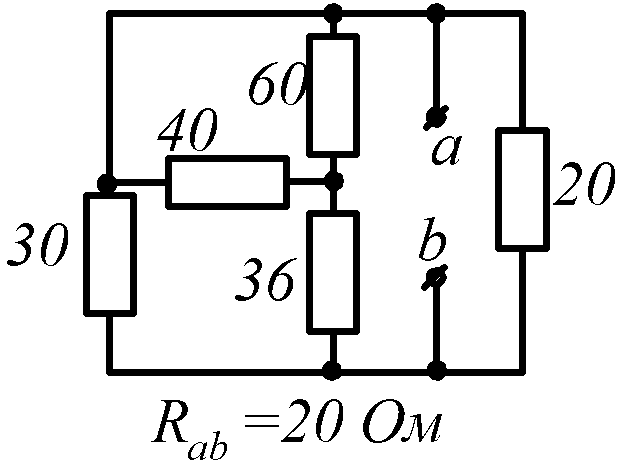
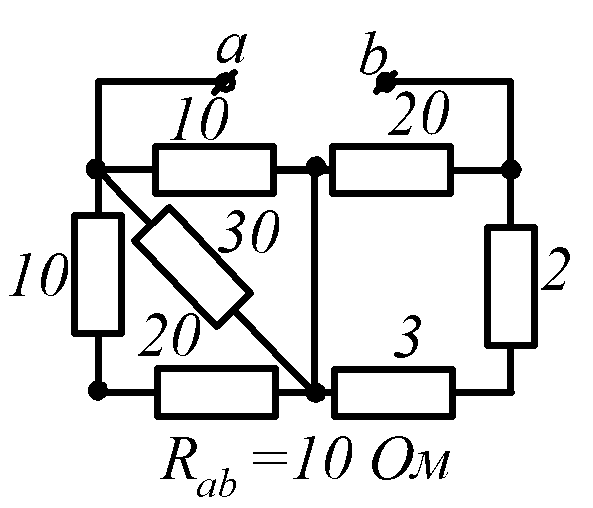
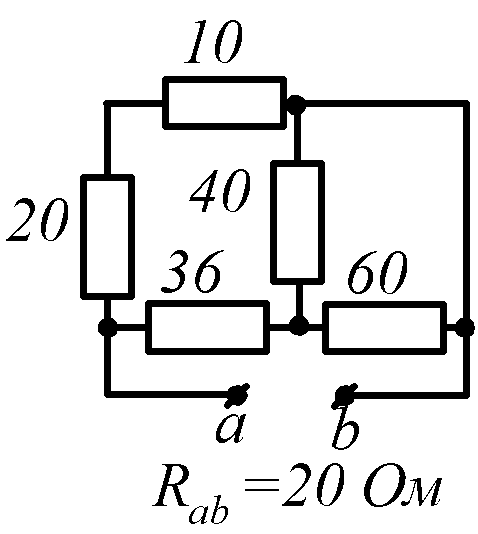
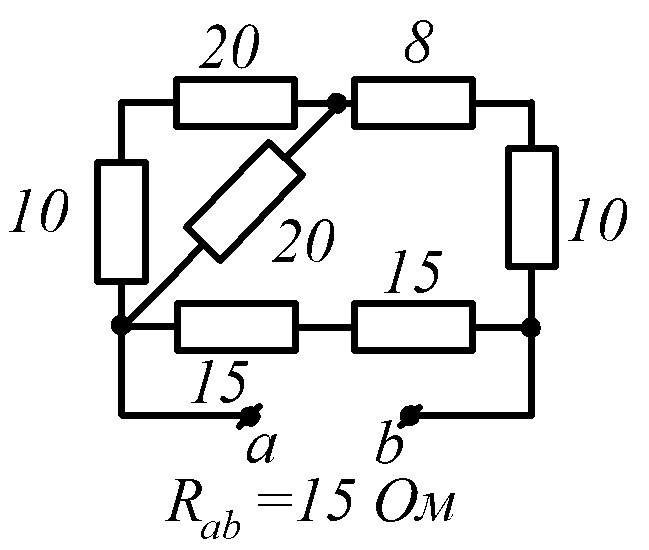
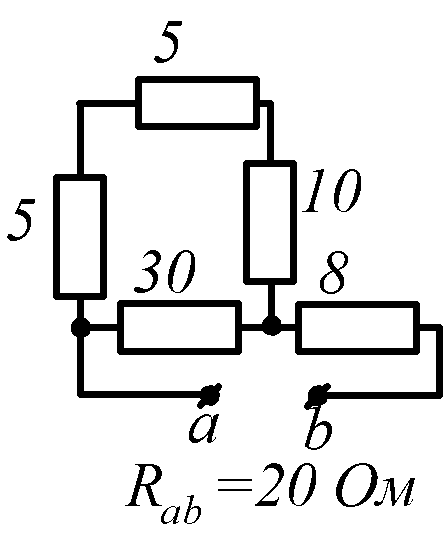
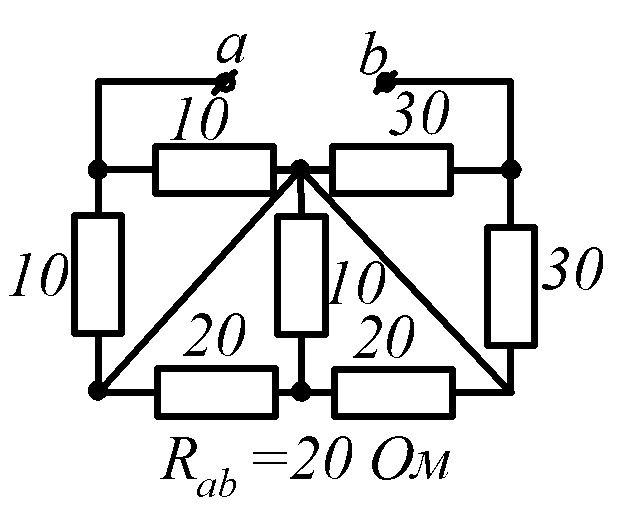
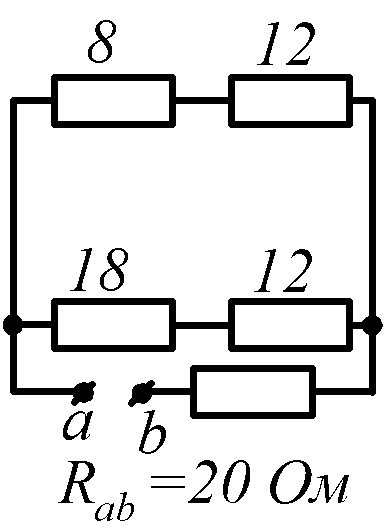
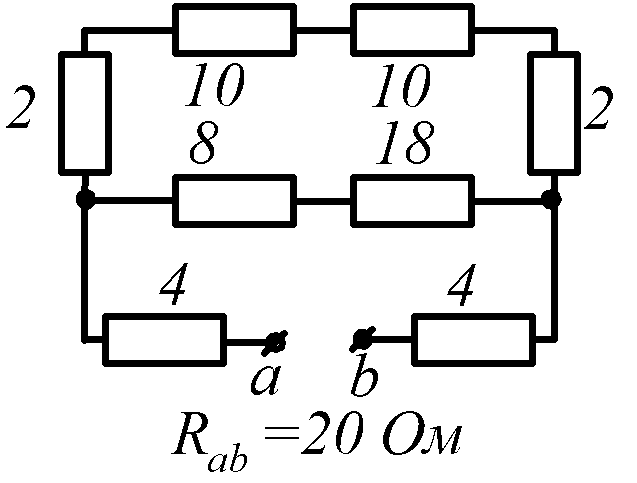
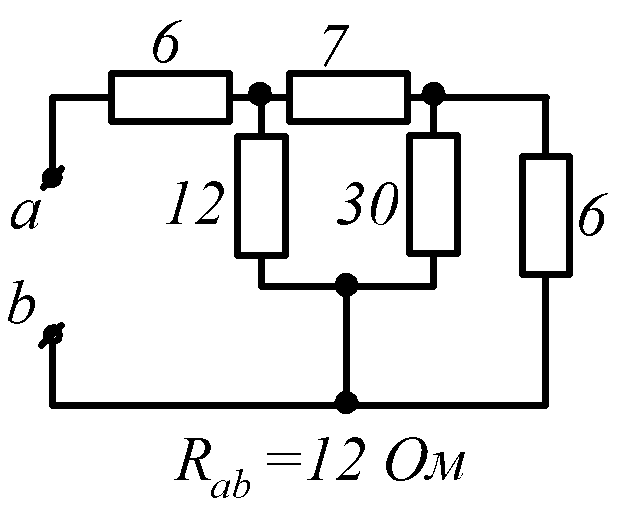
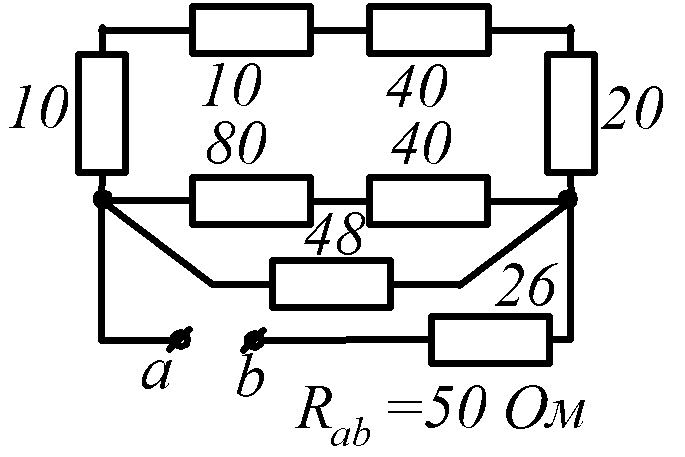
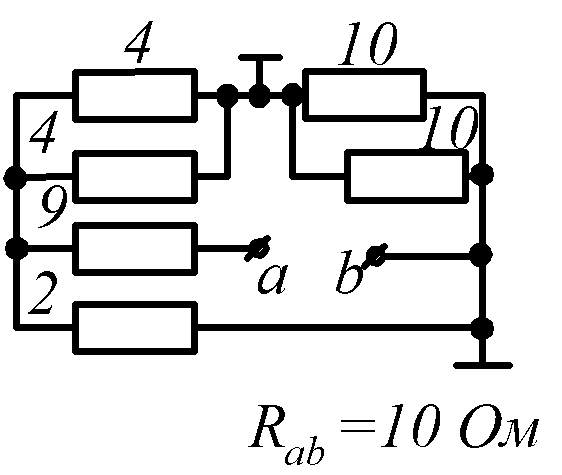
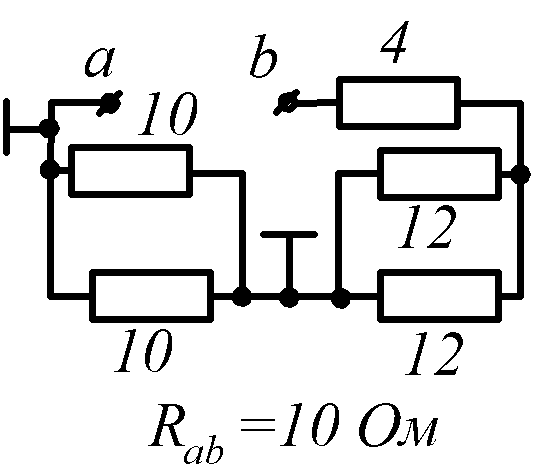
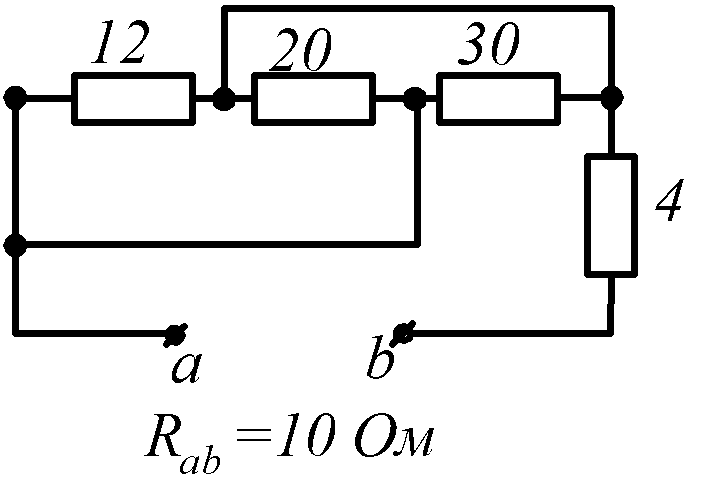
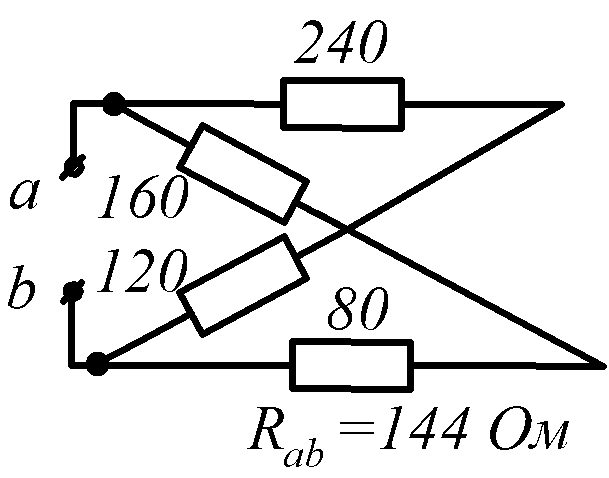
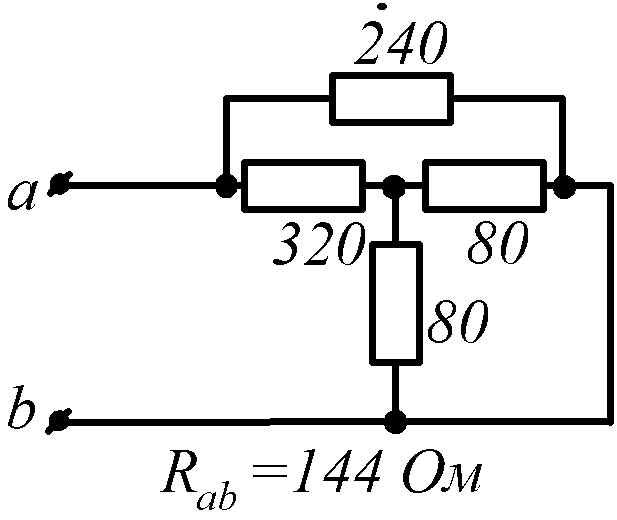
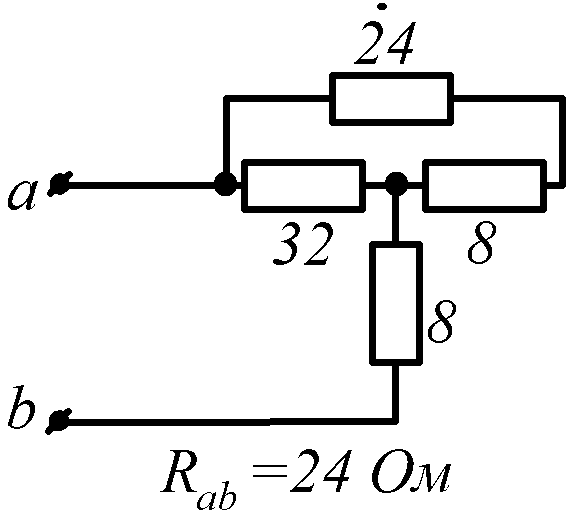
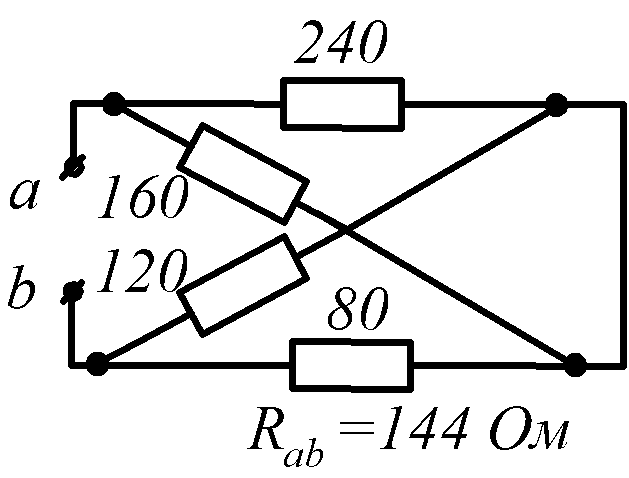
Условие задачи. Определить входное сопротивление цепи (рис.1.32, схемы 1-30). Параметры сопротивлений заданы в Омах. Ответ приведен под схемой.

Знаком обозначена общая точка схемы.

1		6
2		7
3		8
4		9
5		10
Рис. 1.32, лист 1
11		16
12		17
13		18
14		19
15		20
Рис. 1.32, лист 2
21		26
22		27
23		28
24		29
25		30
Рис. 1.32, лист 3

Пример решения. Определить входное сопротивление цепи, приведенной на рис.1.36,а, если Ом, Ом, Ом, Ом, Ом.

Решение. Точки, отмеченные , можно объединить в одну точку общим проводом (показан штриховой линией). Тогда расчетная схема примет вид схемы на рис. 1.36,б, на которой резистор закорочен, а и ; и ; и параллельны между собой:

Ом;

Ом; Ом;

В результате получим схему, приведенную на рис. 1.33-в, на которой и последовательное соединение с эквивалентным сопротивлением

Ом.

Между точками 1 и б - параллельное соединение из и

.

Окончательно и соединены последовательно, что дает входное сопротивление цепи относительно точек а и б

Ом.

1.3.2. Определение токов и напряжений

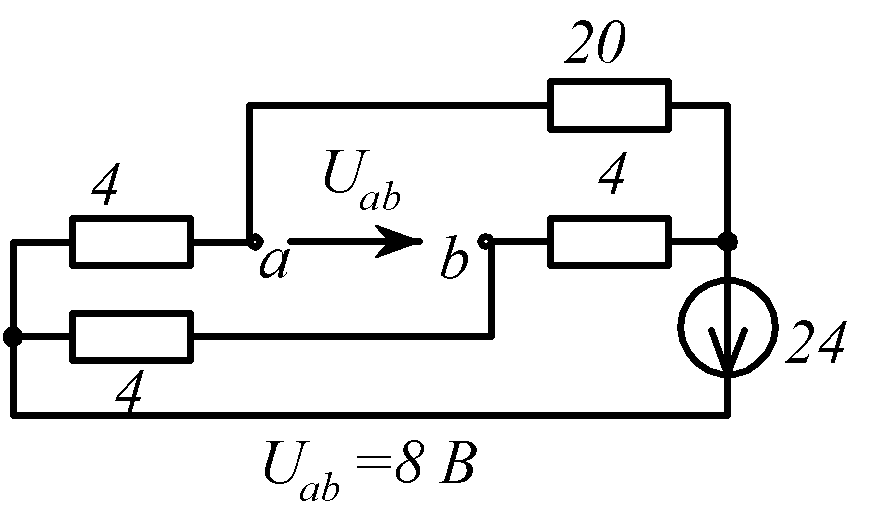
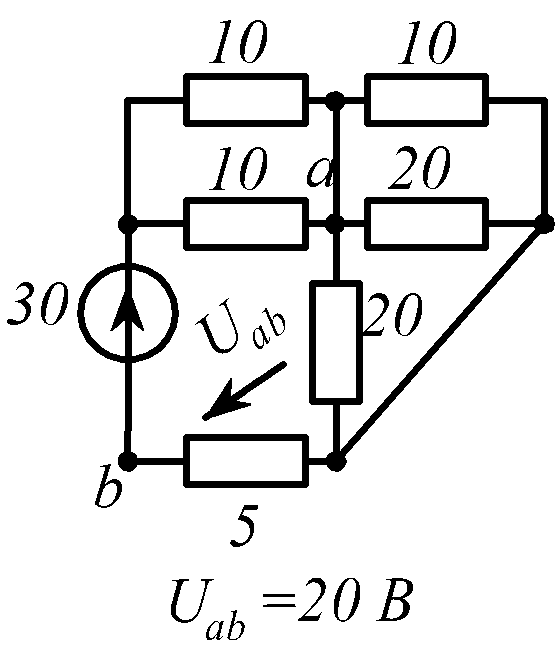
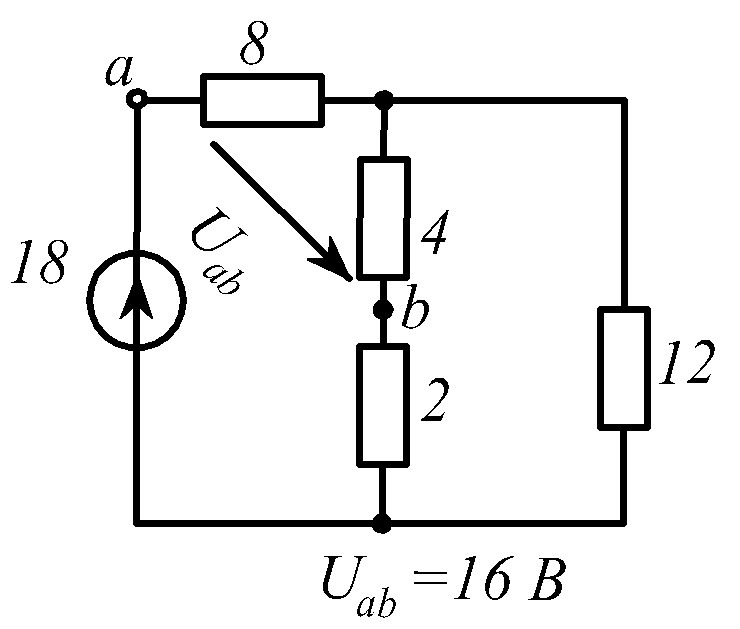
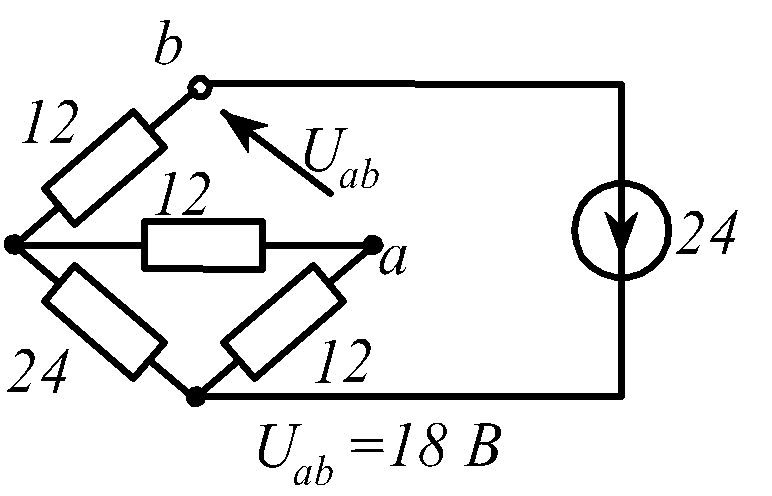
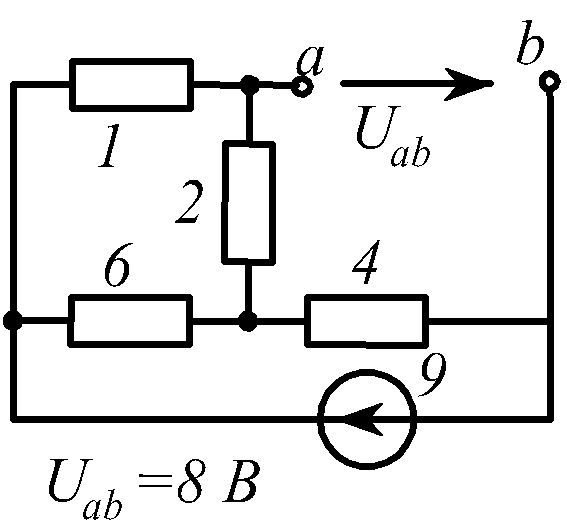
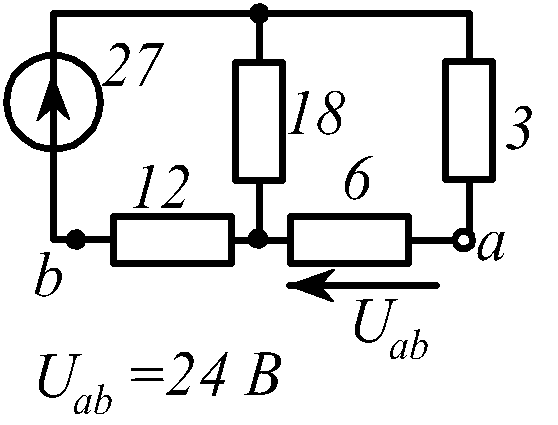
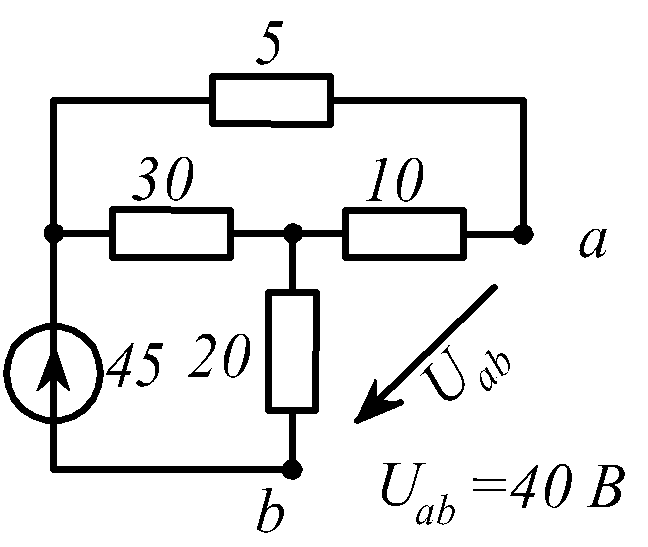
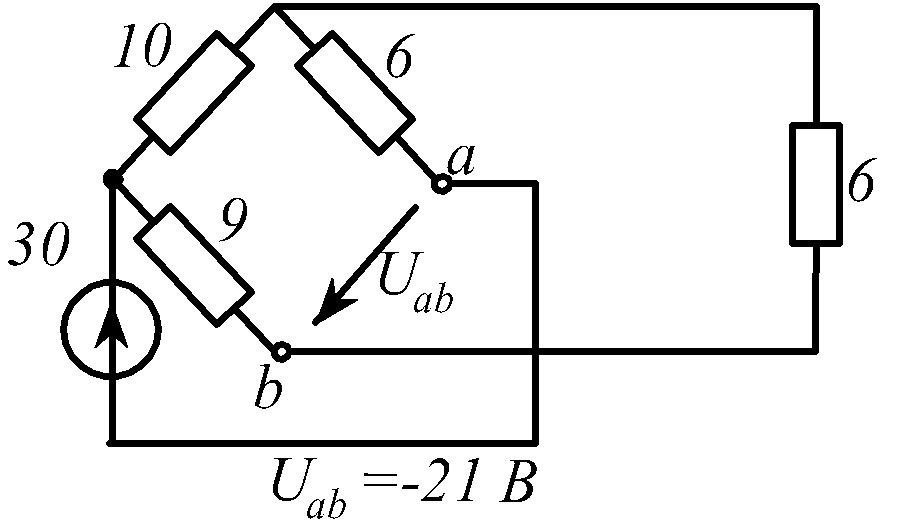
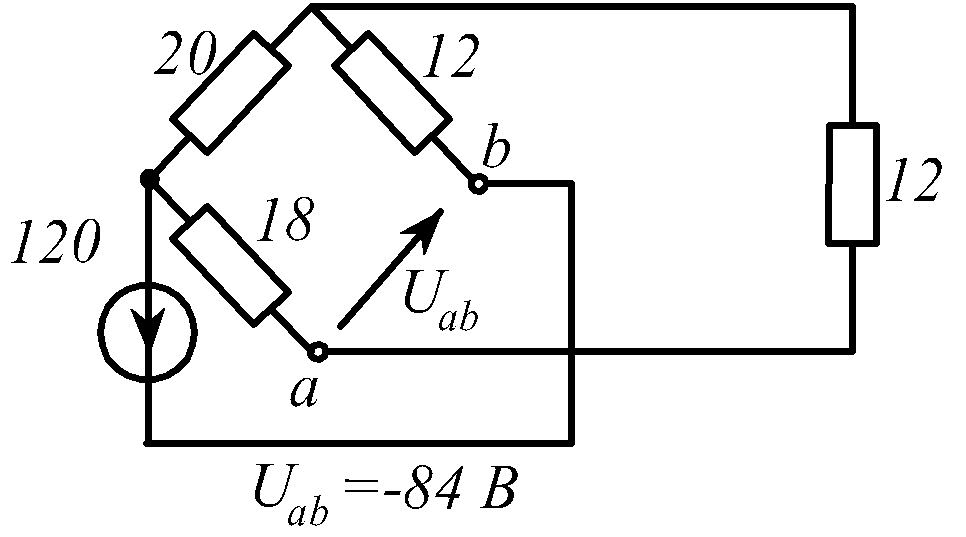
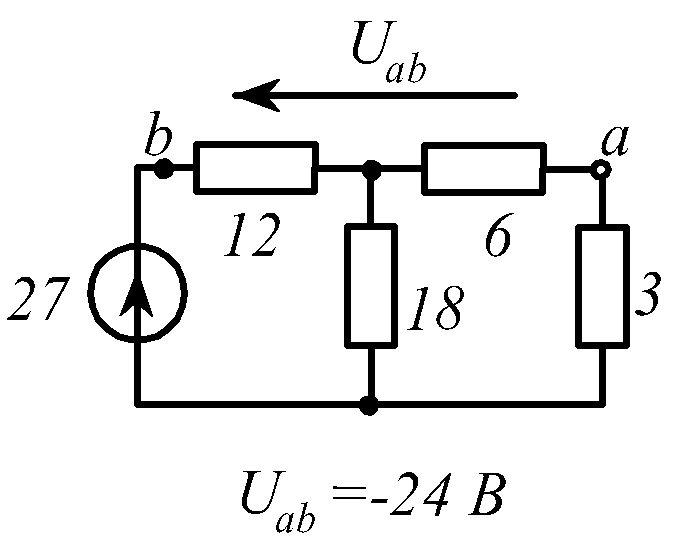
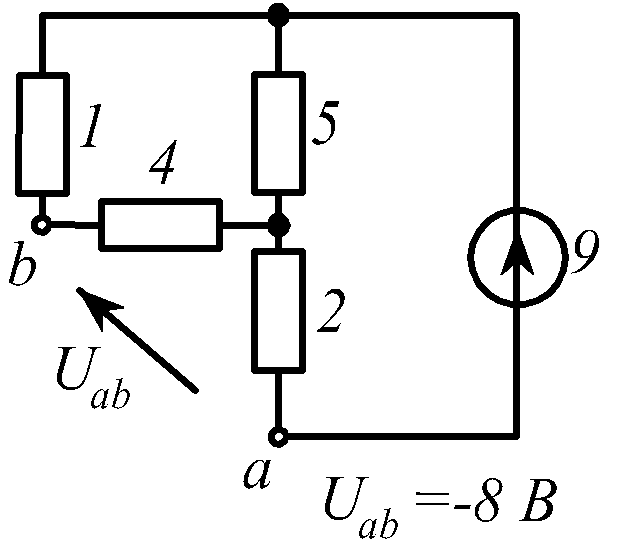
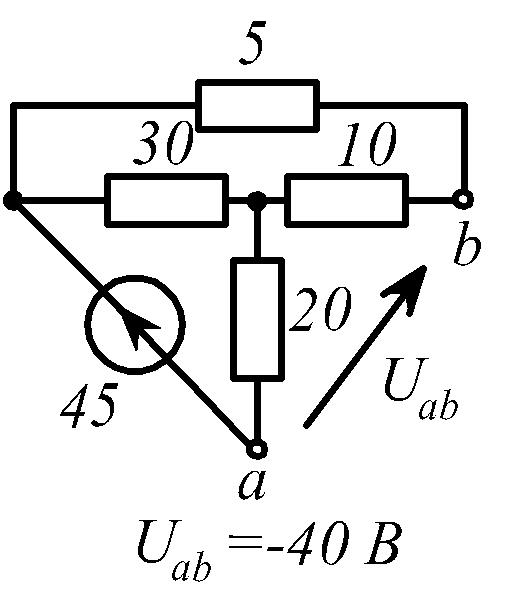
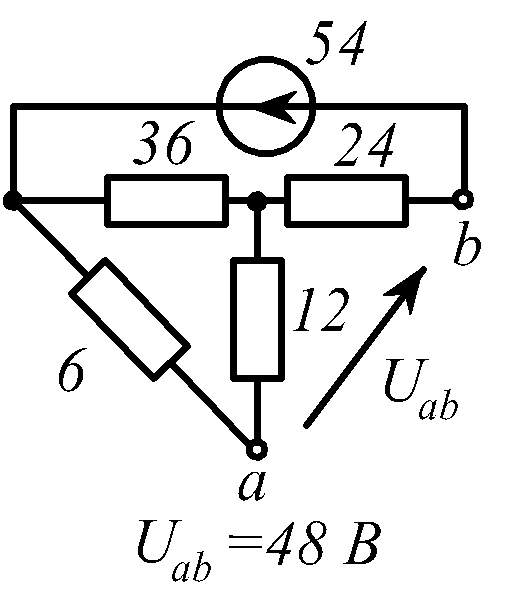
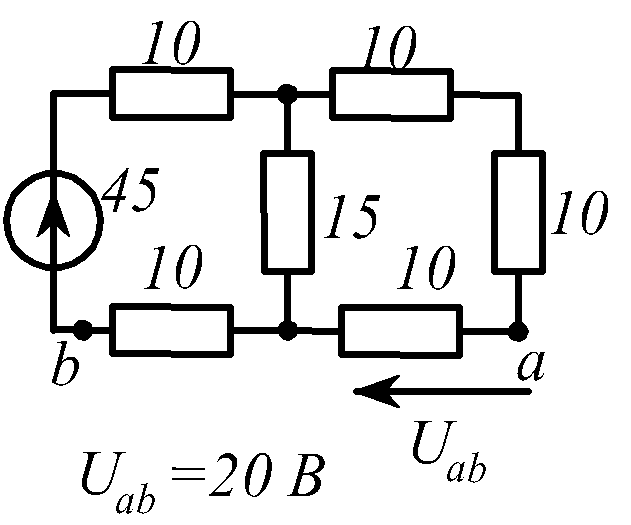
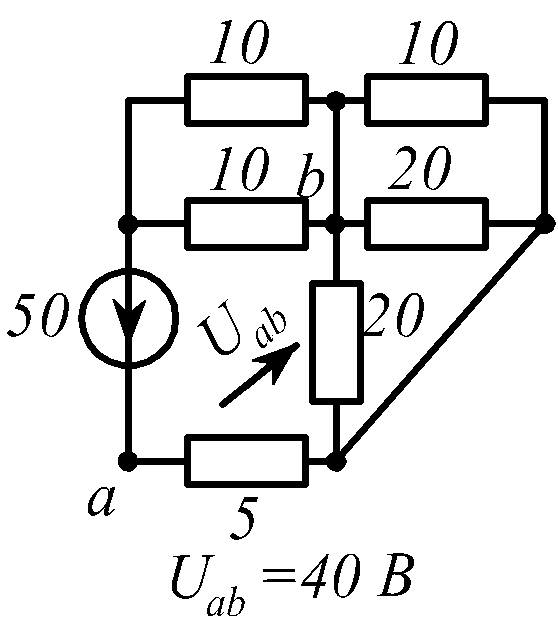
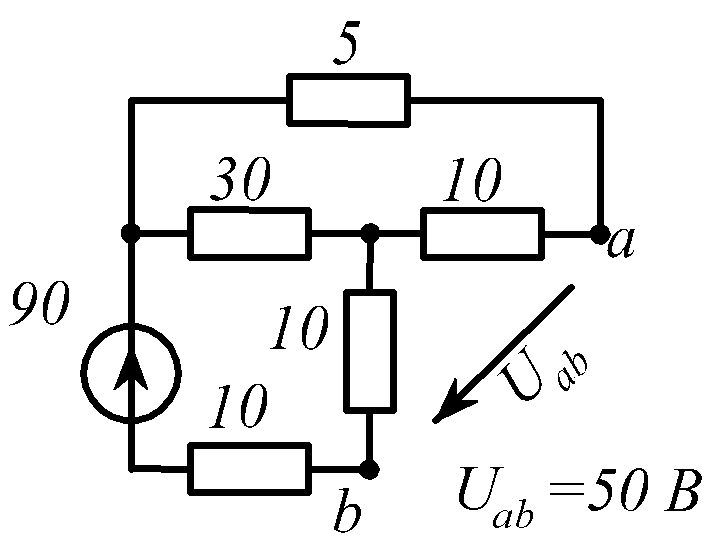
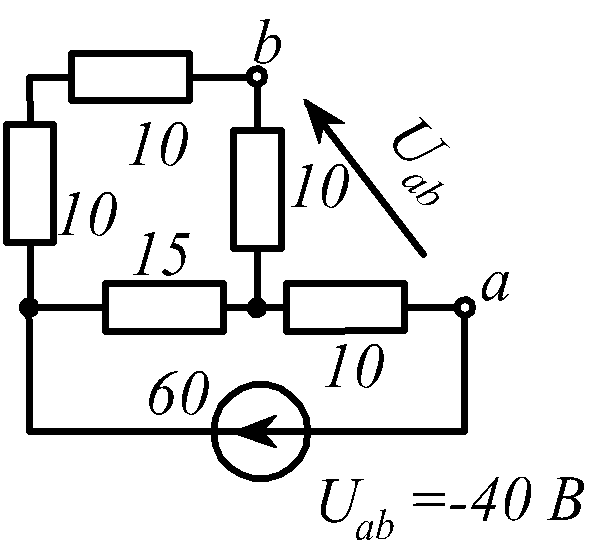
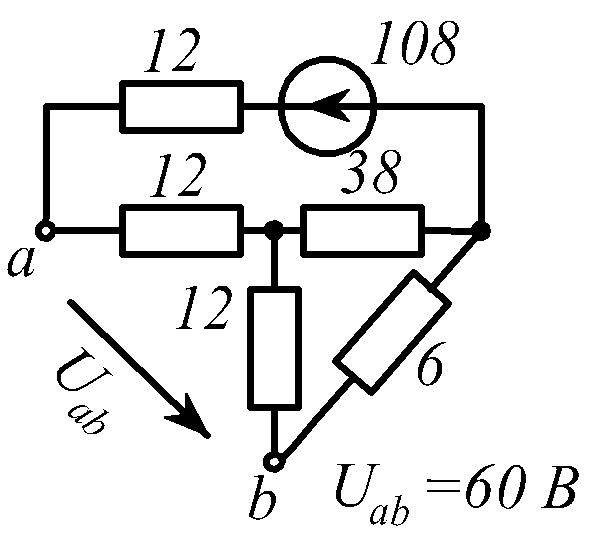
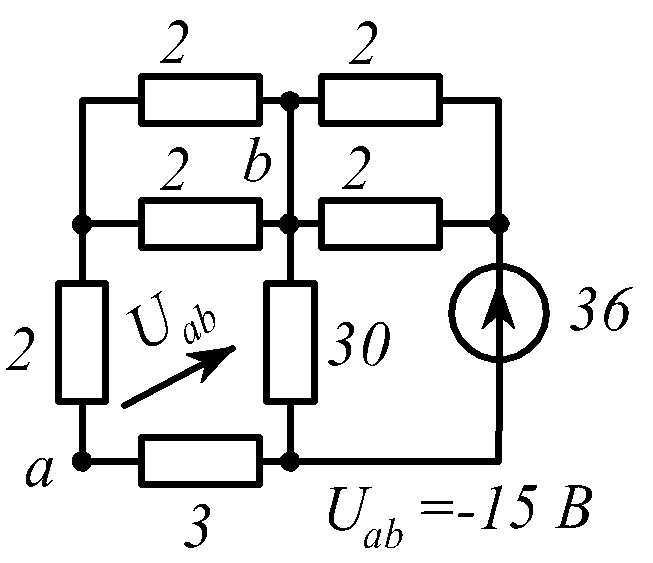
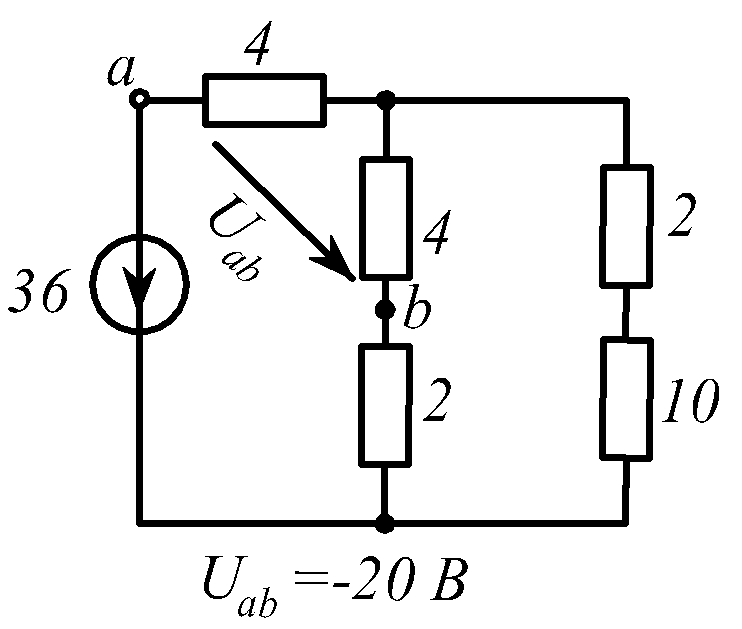
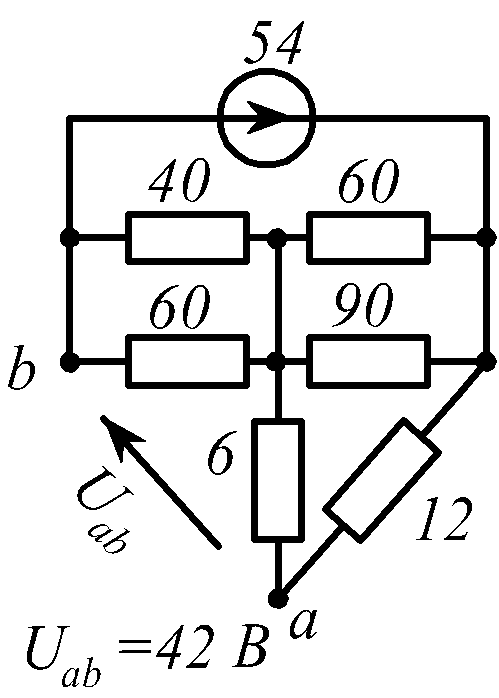
Условие задачи. В заданной цепи (рис. 1.34, схемы 1-30) действует источник постоянной ЭДС E. Определить токи ветвей и напряжение Составить баланс мощностей. ЭДС задана в Вольтах, резисторы - в Омах.

О твет приведен под схемой.

1		3
2		4
Рис. 1.34, лист 1
5		10
6		11
7		12
8		13	◦
9		14
Рис. 1.34, лист2
15		19
16		20	60
17		21
18		22
Рис. 1.34, лист3
23		27
24		28
25		29
26		30
Рис. 1.34, лист 4

Пример решения. В расчетной схеме, приведенной на рис.1.35, заданы Е=120 В, R₁=R₄=40 Oм_, R₂=R₃=60 Oм, R₄=50 Oм.

Определить все токи и напряжение U_ab. Составить баланс мощностей.

Решение.

Ом;

Ом;

Ом;

Ом;

А;

В;

А;

А;

А; А.

Напряжение определим двумя путями:

а) через разность потенциалов

В;

б) по второму закону Кирхгофа, например, для контура abda или для контура abca B.

Проверим расчет балансом мощностей. Отдаваемая источником мощность Вт. Мощность нагрузок Вт.

Так как , то имеет место баланс мощностей.