1.1.8. Баланс мощностей
На основании закона сохранения энергии количество теплоты, выделяющейся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источниками питания.
Уравнение баланса мощностей имеет вид:
(1.6)
В левой части равенства записана алгебраическая сумма произведений ЭДС источников на токи, протекающие через эти источники, и произведений токов источников тока на напряжения на их зажимах.
П
римеры
для определения знаков слагаемых
приведены на рис.1.7.
В правой части уравнения баланса мощностей записана арифметическая сумма произведений сопротивлений на квадраты токов, протекающих по этим сопротивлениям.
1.1.9. Задачи для самостоятельного решения
Задача 1. Предел измерения амперметра - 50 мА. Число делений шкалы - 25. Стрелка отклонилась на 20 делений. Определить показание амперметра.
Ответ: I = 40 мA.
Задача 2. Предел измерения вольтметра - 10 В. Число делений шкалы - 20. Стрелка отклонилась на 17 делений. Определить показание вольтметра.
Ответ: U = 8,5 В.
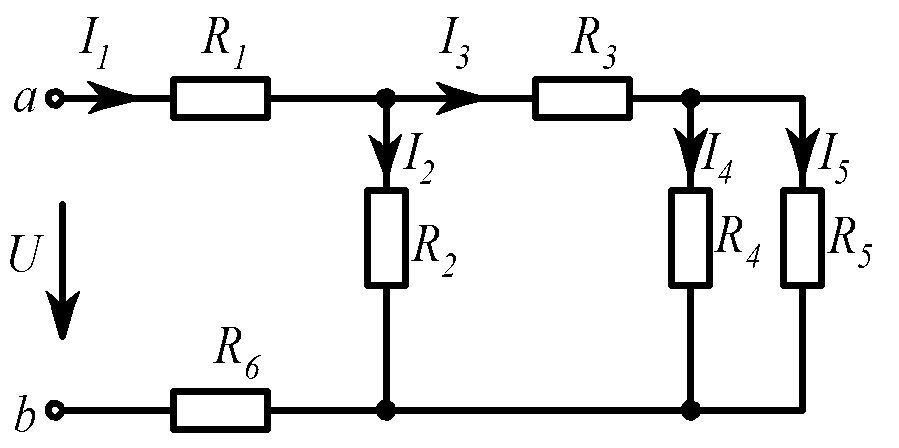
Задача 3(рис. 1.8).
R1 = 4 Ом, |
R2 = 2 Ом, |
|
R3 = 1 Ом, |
R4 = 2 Ом, |
|
R5 = 2 Ом, |
R6 = 5 Ом, |
|
U = 40 B. |
Rab, I1, I2, I3, I4, I5. |
|
Найти: |
||
Ответ: |
Rab = 10 Ом, I1 = 4 А, I2 = 2 А, I3 = 2 А, I4 = 1 А, I5 = 1 А. |
Рис. 1.8 |
|
Задача 4(рис. 1.9).
-
R1 = 3 Ом,
R2 = 3 Ом,
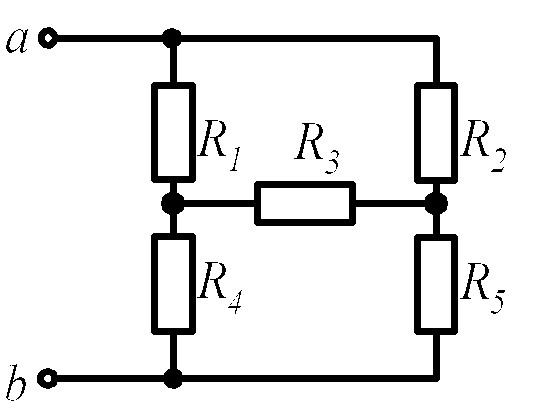
R3 = 3 Ом,
R4 = 1 Ом,
R5 = 1 Ом.
Найти:
Rab.
Ответ:
Rab = 2 Ом.
Рис. 1.9
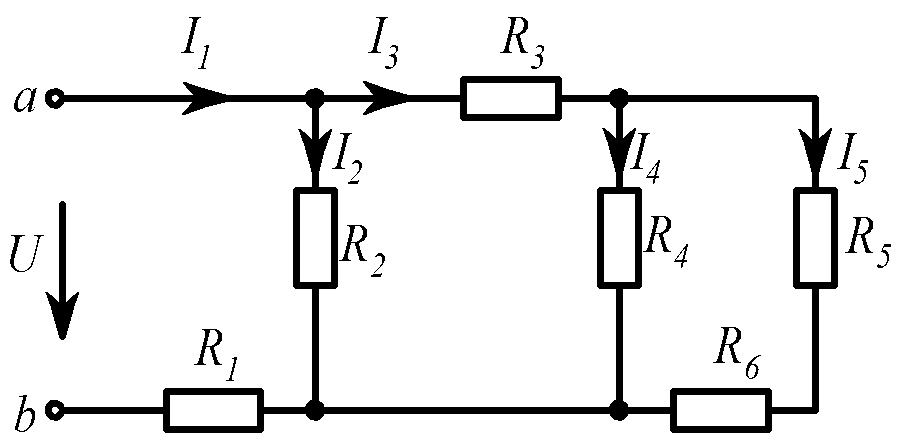
Задача 5 (рис. 1.10).
|
R1 = 7 Ом, |
R2 = 6 Ом, |
R3 = 4 Ом, |
R4 = 4 Ом, |
|
R5 = 2 Ом, |
R6 = 2 Ом, |
|
U = 40 B. |
|
|
Найти: |
Rab, I1, I2, I3, I4, I5. |
|
Рис. 1.10 |
Ответ: |
Rab = 10 Ом, I1 = 4 А, I2 = 2 А, I3 = 2 А, I4 = 1 А, I5 = 1 А. |
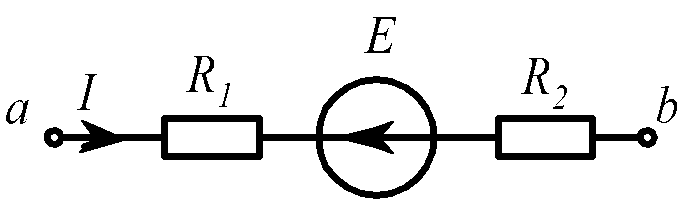
Задача 6 (рис. 1.11).
|
φa = 25 B, |
φb = 5 B, |
R1 = 10 Ом, |
R2 = 20 Ом, |
|
E = 10 B. |
|
|
Рис. 1.11 |
Найти: |
I. |
|
Ответ: |
I = 1 A. |
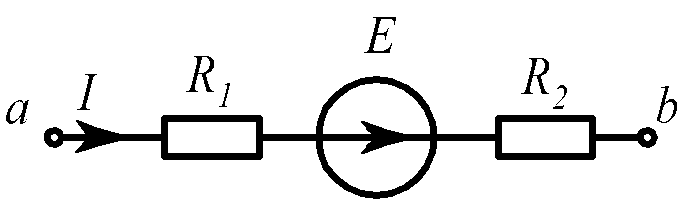
Задача 7 (рис. 1.12).
|
I = 1 A, |
E = 10 B, |
R1 = 3 Ом, |
R2 = 7 Ом. |
|
Найти: |
Uab. |
|
Рис. 1.12 |
Ответ: |
Uab = 20 B. |
|
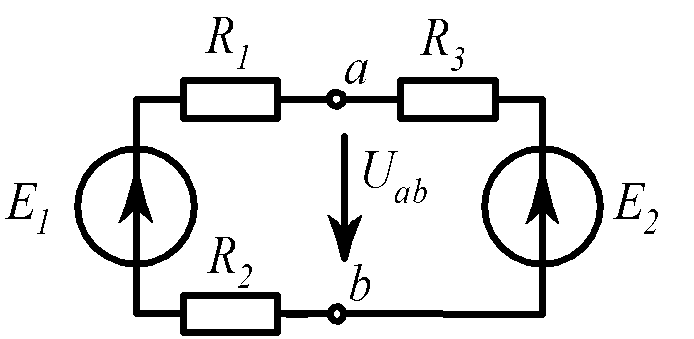
R1 = 3 Ом, |
R2 = 1 Ом, |
R3 = 1 Ом, |
E1 = 10 B, |
|
E2 = 5 B. |
|
|
Найти: |
Uab. |
|
Рис. 1.13 |
Ответ: |
Uab = 6 B. |
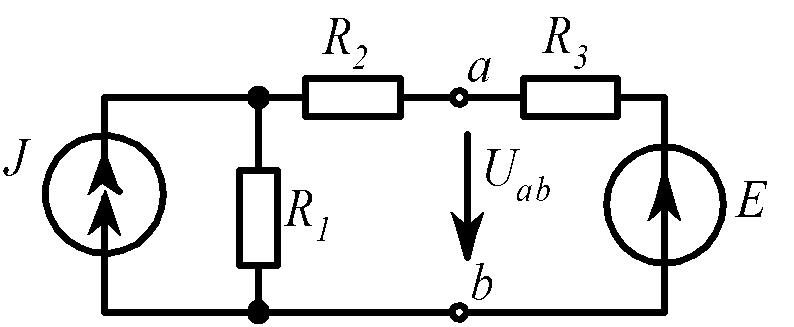
Задача 9 (рис. 1.14).
R1 = 1 Ом, |
R2 = 3 Ом, |
|
R3 = 1 Ом, |
J = 10 A, |
|
E = 5 B. |
|
|
Найти: |
Uab. |
|
Ответ: |
Uab = 6 B. |
Рис. 1.14 |
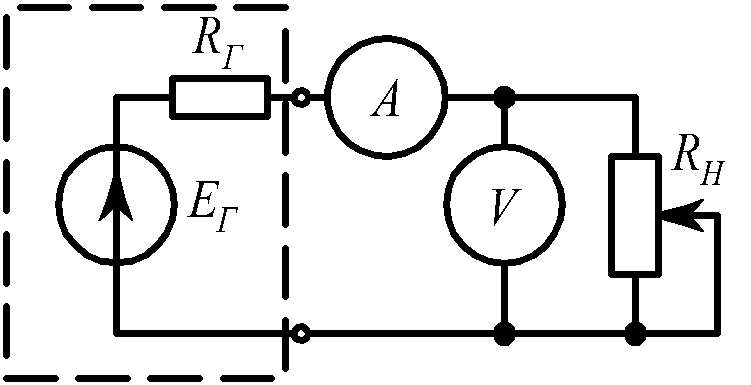
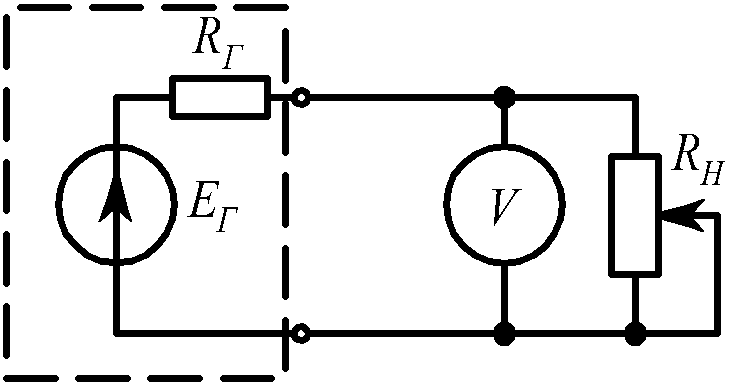
Задача 10 (рис. 1.15).
При одном значении сопротивления нагрузки RН показания амперметра – 1 А, вольтметра – 9,9 В; при другом значении – 2 А и 9,8 В. Измерительные приборы считаем идеальными (RA = 0, RV = ∞). |
|
|
Найти: |
EГ, RГ. |
Рис. 1.15 |
Ответ: |
EГ = 10 B, RГ = 0,1 Ом. |
|
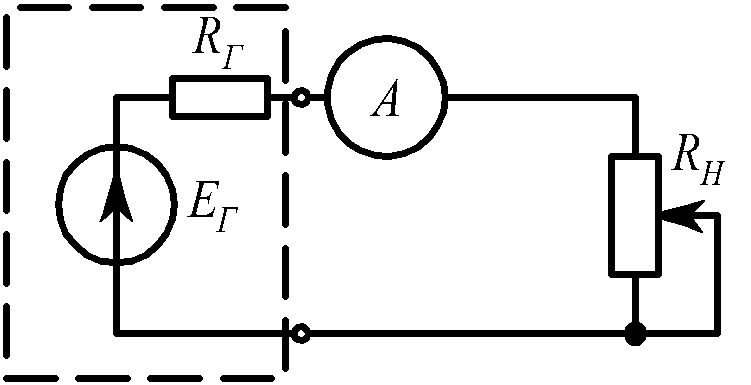
Задача 11 (рис. 1.16).
При сопротивлении нагрузки RН1 = 9 Ом амперметр показал ток I1 = 1 A; при RН2 = 4 Ом, I2 = 2 A. RA = 0,9 Ом. |
|
|
Найти: |
EГ, RГ. |
|
Ответ: |
EГ = 10 B, RГ = 0,1 Ом. |
Рис. 1.16 |
Задача 12 (рис. 1.17).
|
При сопротивлении нагрузки RН1 = 10 Ом вольтметр показал напряжение U1 = 9,9 B; при RН2 = 4,92 Ом, U2 = 9,8 B. RV = 980 Ом. |
|
Рис. 1.17 |
Найти: |
EГ, RГ. |
|
Ответ: |
EГ = 10 B, RГ = 0,1 Ом. |
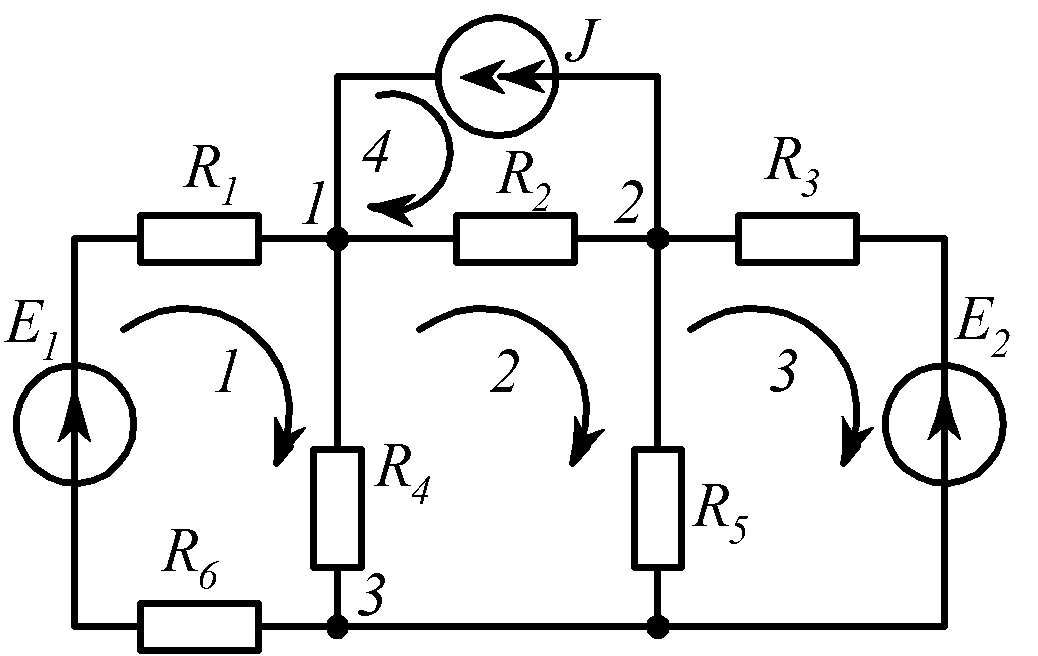
Задача 13 (рис. 1.18).
|
R1 = 1 Ом, |
R2 = 2 Ом, |
R3 = 2 Ом, |
|
R4 = 1 Ом, |
R5 = 2 Ом, |
R6 = 1 Ом, |
||
E1 = 2 B, |
E2 = 6 B, |
J = 2 A. |
||
Найти: |
R11, R12, R22, R21, R23, R33, R32, E11, E22, E33, G11, G12, G22, J11, J22. |
|||
Рис. 1.18 |
|
|
||
Ответ: |
R11 = 3 Ом, R12 = –1 Ом, R22 = 5 Ом, R21 = –1 Ом, R23 = –2 Ом, R33 = 4 Ом, R32 = –2 Ом, E11 = 2 В, E22 = 0 В, E33 = –6 В, G11 = 2 См, G12 = –0,5 См, G22 = 1,5 См, J11 = 3 А, J22 = 1 А. |
|||
