1.1.5. Метод узловых потенциалов

В этом методе за неизвестные принимают потенциалы узлов схемы, а токи ветвей находят по закону Ома.

Рассмотрим правила формирования уравнений на примере схемы, приведенной на рис.1.4, в которой известны величины ЭДС и ток источника тока, а также все сопротивления.

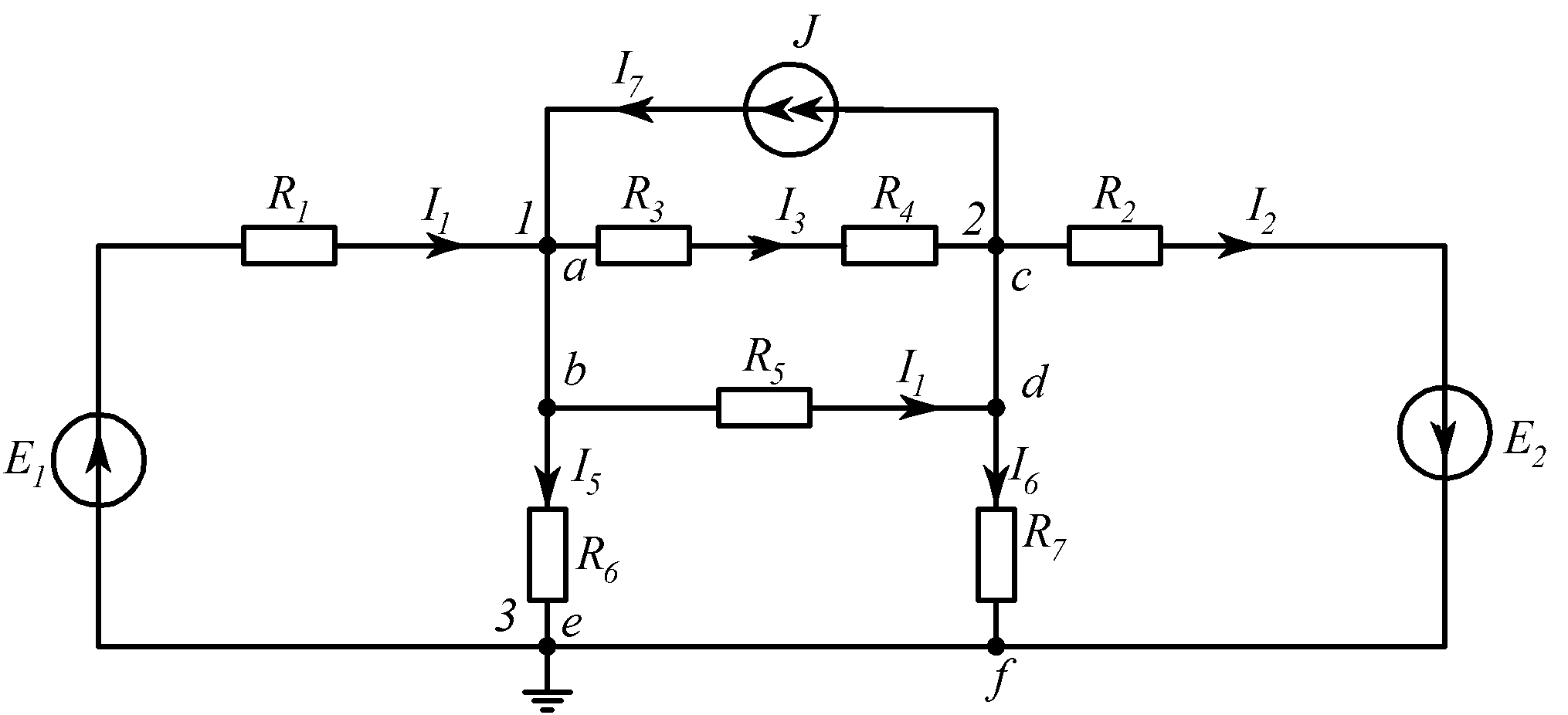
Рис. 1.4

В этой схеме два неизвестных потенциала: и , поскольку , , , а потенциал одного из узлов, в данном случае , принимается равным нулю, что на схеме обозначают заземлением узла 3 - .

Запишем уравнения по первому закону Кирхгофа, предварительно выбрав направления токов в ветвях:

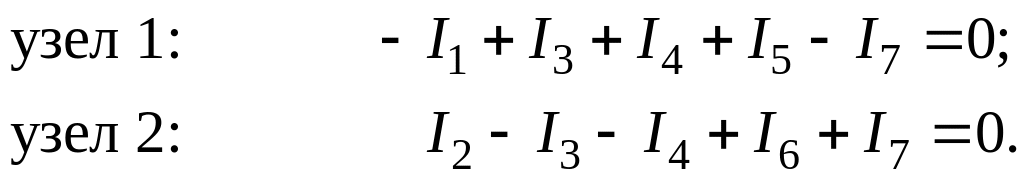(1.3)

Выразим токи ветвей через потенциалы узлов:

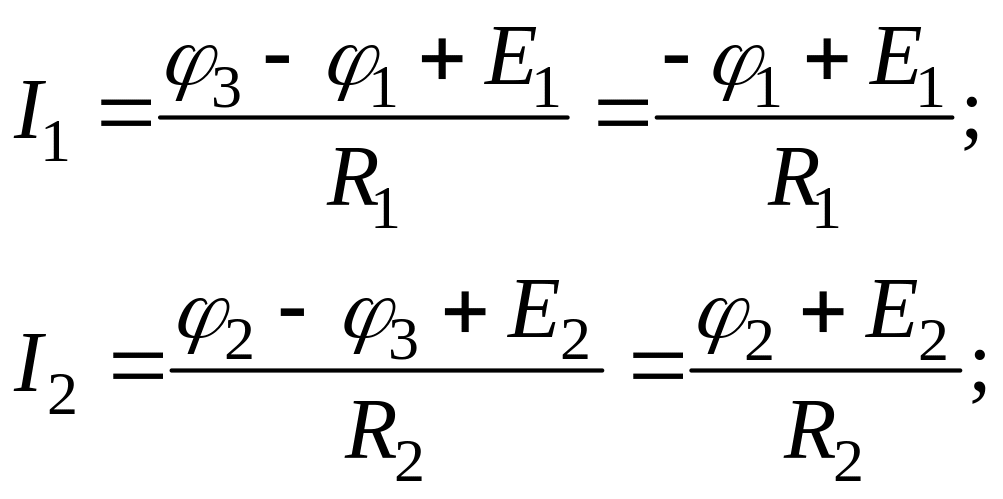
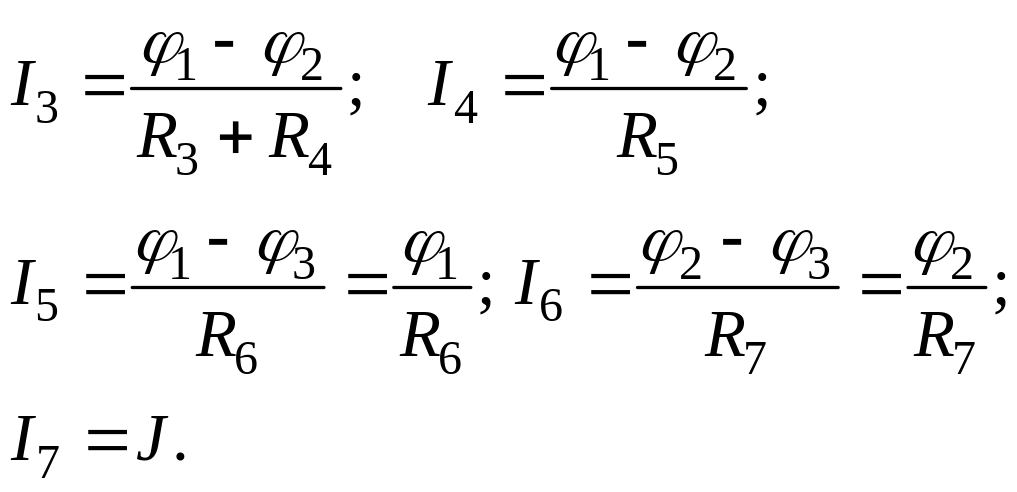
и подставим в систему (1.3):

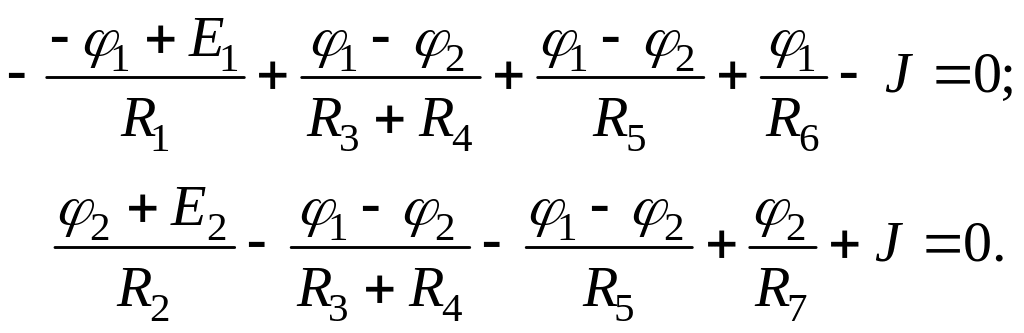
После группировки получим:

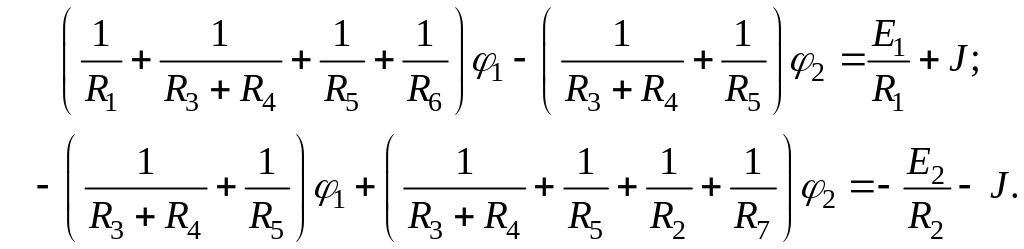
В общем виде:

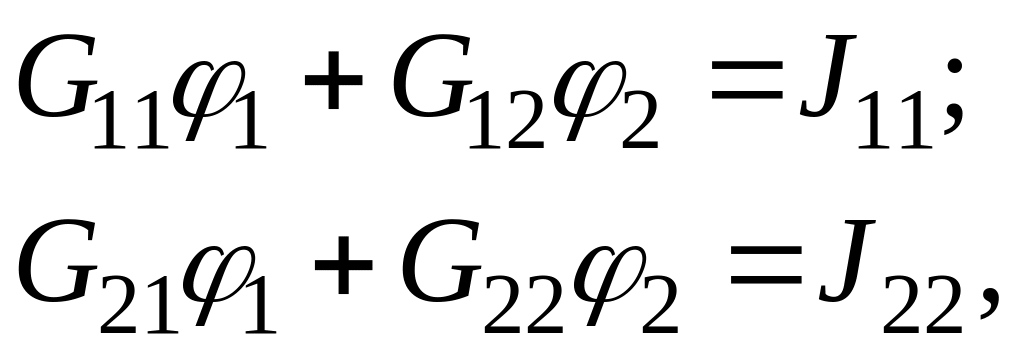(1.4)

где , - собственные (узловые) проводимости узлов 1 и 2, каждая из которых равна сумме проводимостей ветвей, сходящихся в данном узле;

, - общая проводимость - взятая со знаком "минус" сумма проводимостей ветвей, соединяющих узлы 1 и 2 (проводимость ветви, содержащей источник тока, равна нулю);

, - задающие (узловые) токи узлов 1 и 2, каждый из которых равен алгебраической сумме произведений ЭДС на проводимости ветвей, в которых они находятся (рассматриваются ветви, подключенные к данному узлу), и алгебраической сумме токов источников тока, подключенных к данному узлу. Знаки слагаемых: "плюс"- если направление ЭДС (источника тока) к узлу, "минус"- если направление ЭДС (источника тока) от узла.

1.1.6. Последовательность определения токов ветвей методом узловых потенциалов

1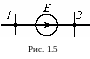 ) Записывается система уравнений в общем виде. Число уравнений системы на единицу меньше числа узлов схемы. Если в схеме содержится ветвь с источником ЭДС без сопротивлений (рис.1.5), то . Приняв , получим .

2) Определяются коэффициенты при неизвестных –

собственные и общие проводимости, а также задающие токи узлов.

3) Рассчитываются потенциалы узлов.

4) Выбираются направления токов ветвей.

5) Определяются токи ветвей.

1.1.7. Определение параметров эквивалентного активного двухполюсника (эквивалентного генератора)

При расчетах линейных электрических цепей возможна замена части цепи, содержащей источники ЭДС и тока, относительно зажимов выделенной ветви ab (рис.1.6,а) активным двухполюсником, состоящим из последовательно соединенных ЭДС и сопротивления. В этом случае указанную ветвь можно рассматривать как нагрузку эквивалентного генератора с ЭДС и сопротивлением .

Эквивалентная ЭДС равна напряжению на зажимах ab при разомкнутой ветви R_Н, т.е. напряжению холостого хода U_XX.

Сопротивление равно входному сопротивлению цепи относительно зажимов ab при разомкнутой ветви R_Н. Источники при этом исключаются из схемы.

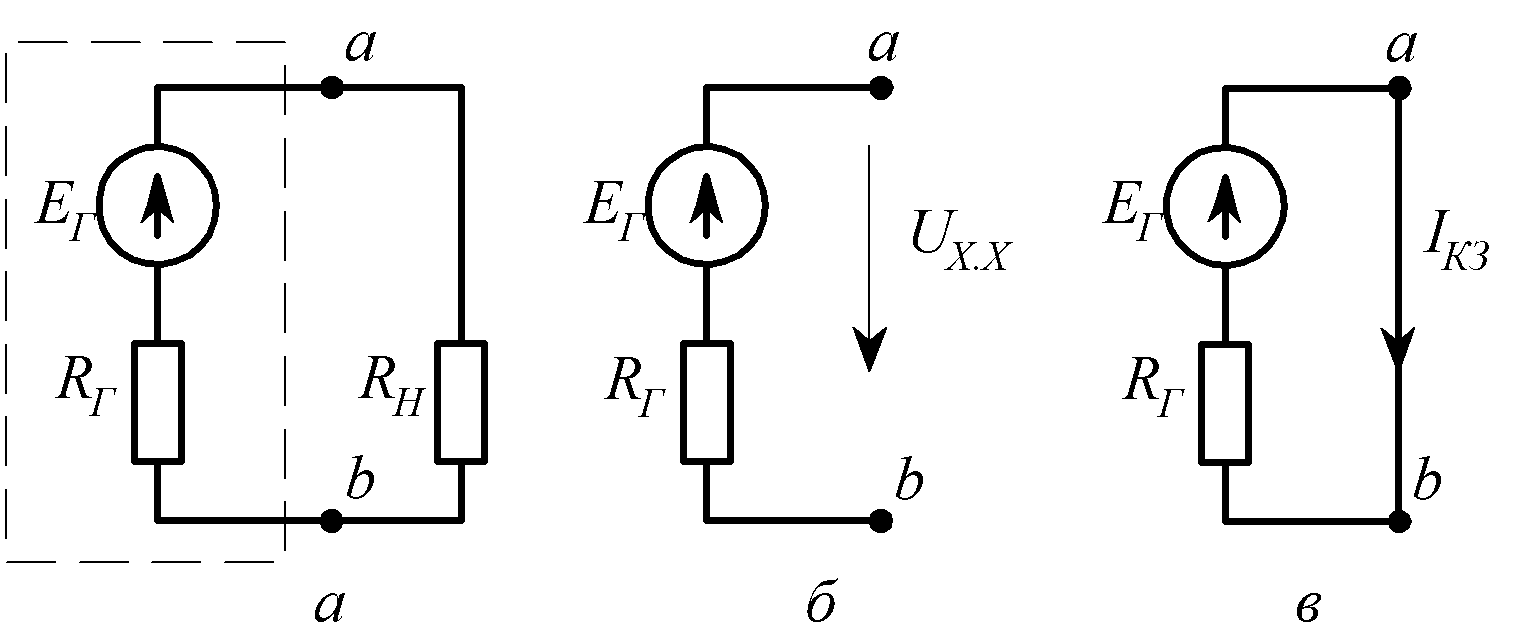
Рис. 1.6

Эквивалентные параметры и могут быть определены опытным путем из режимов холостого хода (рис.1.6,б) и короткого замыкания (рис.1.6,в):

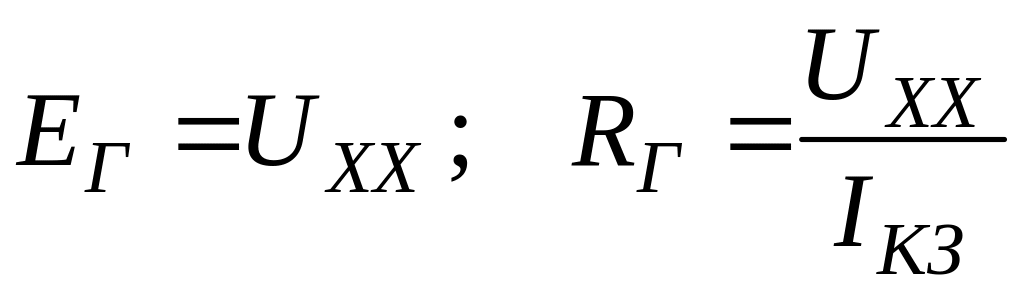. (1.5)