2. Переходный процесс при переменной эдс

Принужденные составляющие токов и напряжений в электрической цепи в установившемся режиме изменяются по синусоидальному закону. Для определения эти законов используем символический метод расчета. Для удобства расчет проведем в амплитудных значениях токов и напряжений.

Представим ЭДС в символическом виде:

.

Определим ток в первой ветви:

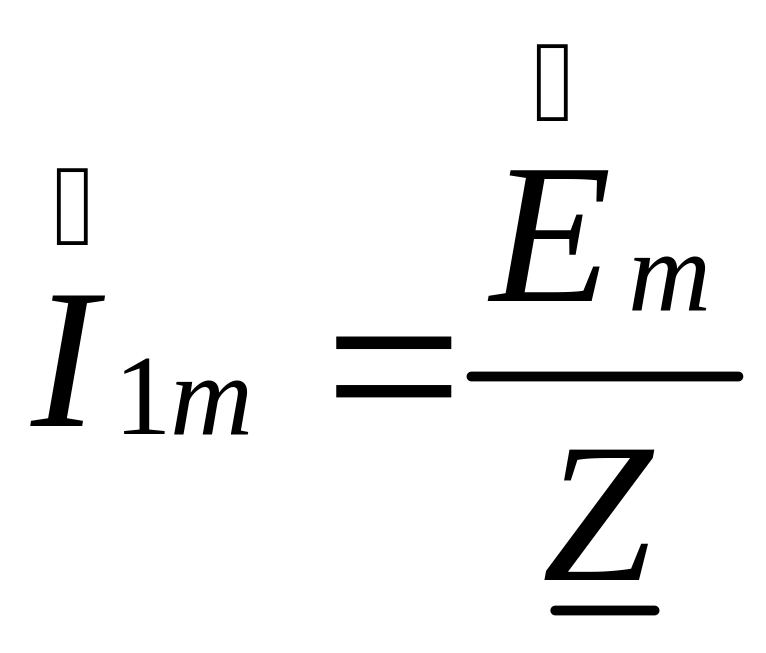(3.62)

где - полное сопротивление электрической цепи.

Составим формулу для определения полного сопротивления электрической цепи:

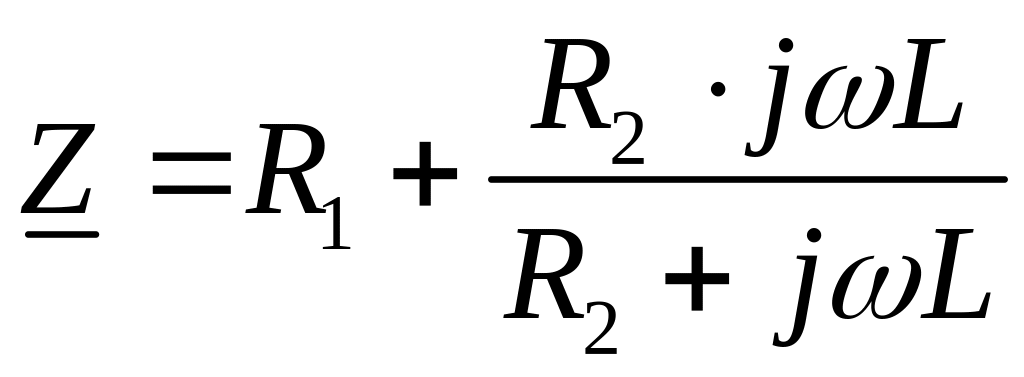(3.63)

Подставив заданные значения в формулу (3.63), получим значение полного сопротивления:

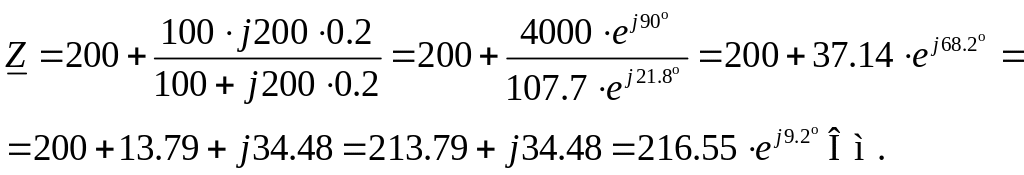
Определим ток в первой ветви, подставив в формулу (3.62) значения полного сопротивления и ЭДС:

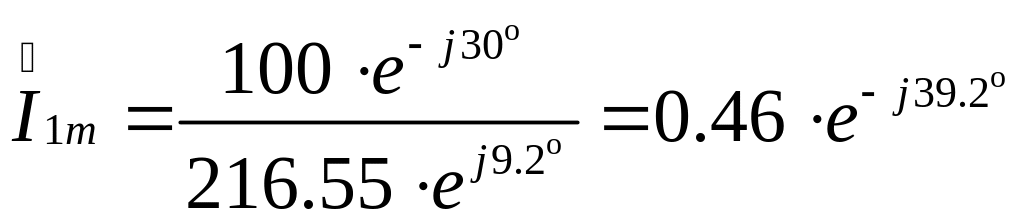А.

Закон изменения принужденной составляющей первого тока примет вид:

А.

Для определения принужденных составляющих токов в индуктивности и во второй ветви, а так же принужденной составляющей напряжения на индуктивности определим напряжение участка ab:

Определим сопротивление участка ab:

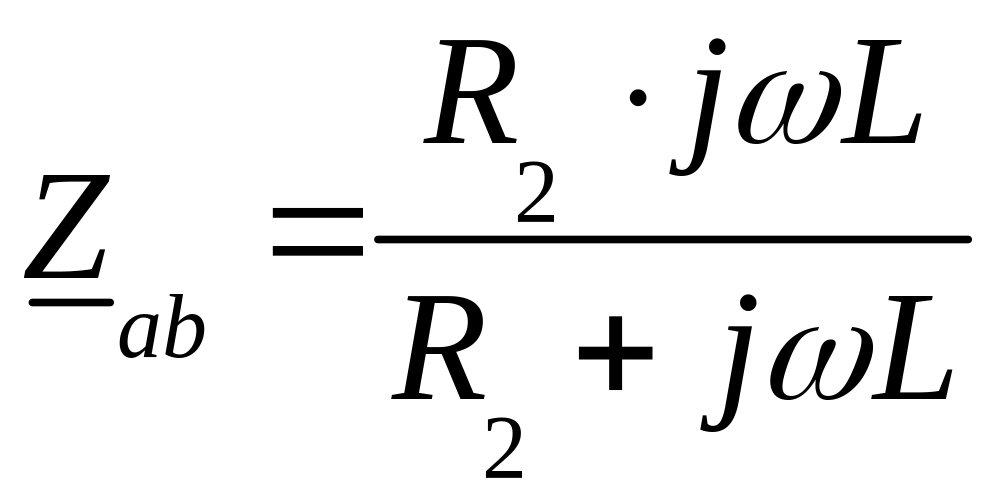. (3.64)

Воспользуемся значениями расчетов, полученных при определении полного сопротивления:

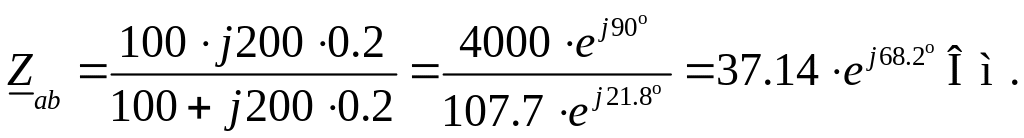
Находим напряжение :

В.

Поскольку индуктивность и сопротивление подключены к узлам ab, то напряжения на этих элементах совпадает с напряжением . Запишем закон изменения принужденной составляющей на индуктивности:

В.

Определим ток во второй ветви, используя закон Ома:

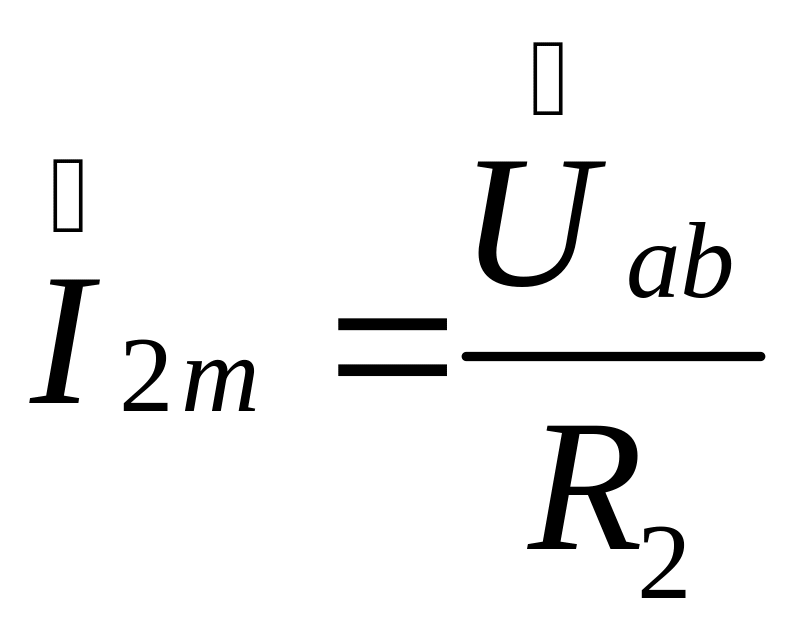(3.65)

Подставив значения напряжения в формулу (3.65) получим ток во второй ветви:

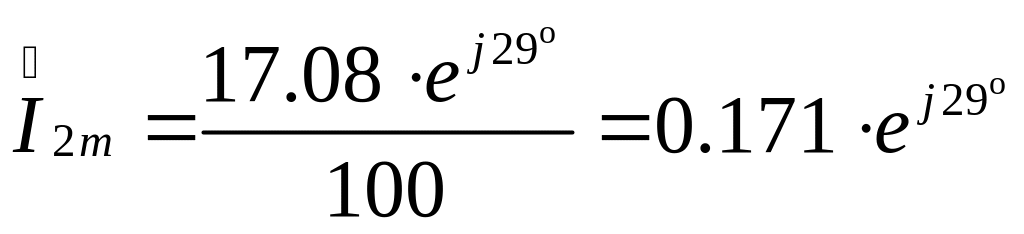
Закон изменения принужденной составляющей второго тока запишем в виде:

А.

Аналогично определим закон изменения принужденной составляющей тока в индуктивности:

,

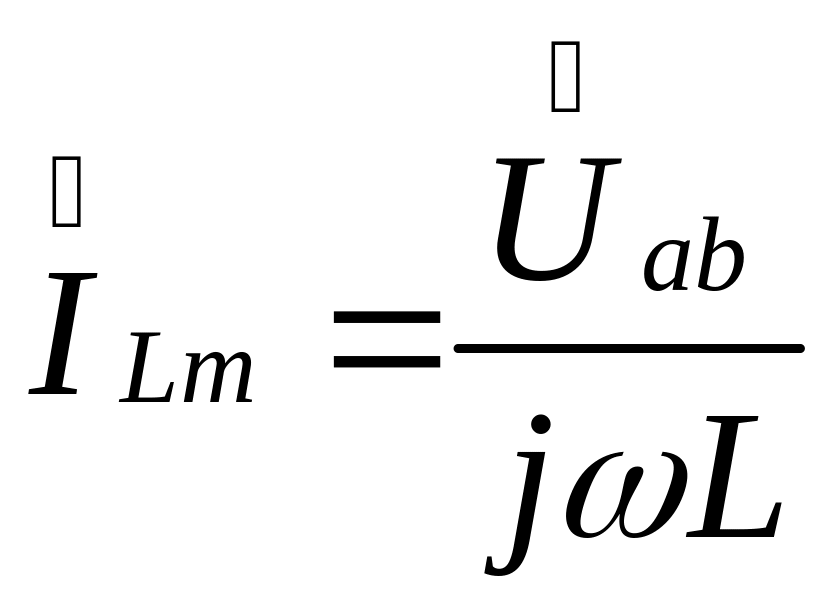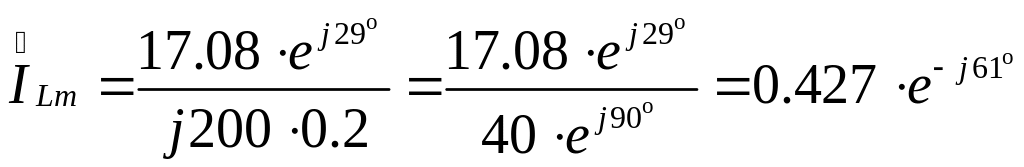А,

А.

Характеристическое уравнение не изменится, так как электрическая цепь осталась прежней. Поэтому используем значение корня характеристического уравнения, полученное в предыдущем пункте:

.

Свободные составляющие токов и напряжений в электрической цепи не зависят от принуждающей ЭДС, а закон их изменения определяется корнями характеристического уравнения и будет иметь вид (см. пункт 3.1.10):

.

Тогда полный закон изменения первого тока примет вид:

(3.66)

Аналогично можно записать законы изменения для других токов и напряжения на индуктивности:

(3.67)

(3.68)

(3.69)

Для определения постоянных интегрирования А₁, А₂, А_L и необходимо найти начальные значения токов и напряжения на индуктивности при t=0₊.

До коммутации в схеме имеют место нулевые начальные значения. Используя первый закон коммутации, получаем:

А.

Составляем систему уравнений для мгновенных значений токов и напряжений непосредственно после коммутации в момент времени t=0₊, используя первый и второй законы Кирхгофа.

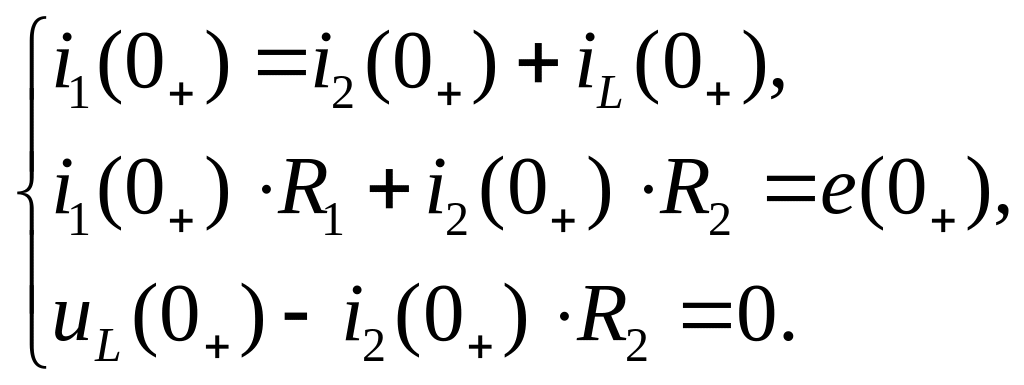(3.70)

Подставив известные значения в систему (3.70), получим:

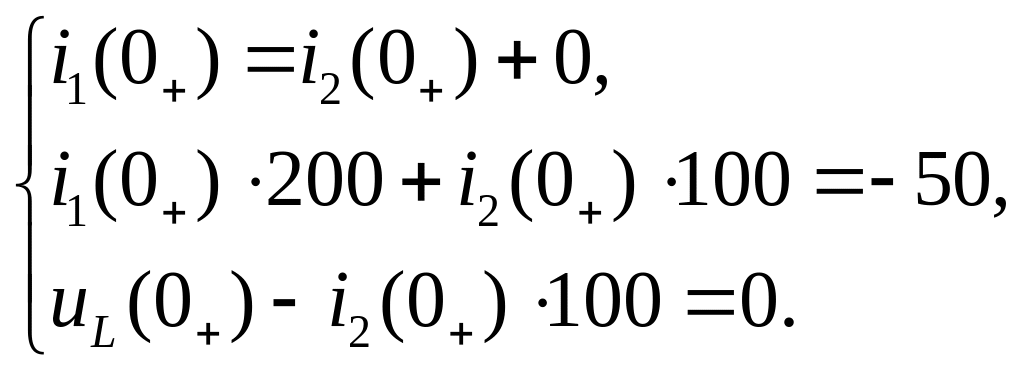(3.71)

Решив систему уравнений (3.71), получим:

А, В.

Подставив полученные начальные значения токов в уравнения (3.66) - (3.69) для момента времени t=0, находим постоянные интегрирования А₁, А₂, А_L и :

А,

А,

А,

В.

А, А, А, В.

В результате получаем законы изменения токов , и напряжения на индуктивности:

А,

А,

А,

А.

Для построения графика токов рекомендуется использовать программу MathCad. Переходный режим характеризуется постоянной времени с (см пункт 3.3.2), а принужденная составляющая (установившийся режим) характеризуется периодом , с. Поэтому для построения графика переходного процесса необходимо оценить отрезки времени: - время переходного процесса и Т - период синусоидальной ЭДС. В нашем случае , а с. Следовательно, переходный процесс закончится меньше чем за период Т. Поэтому для построения графика переходного процесса достаточно взять интервал времени Т или чуть больший, который охарактеризует и принужденную и свободную составляющую. График необходимо строить с шагом .