3.2. Операторный метод расчета переходных процессов

3.2.1. Основные понятия и определения

Введем понятие оригинала и изображения. В ряде случаев для упрощения расчетов производят преобразования, при которых операции умножения, деления и возведения в степень заменяются на сложение, вычитание и умножение соответственно.

При этом можно говорить об оригинале и изображении.

Если к числу 2 применить операцию логарифмирования по основанию 10, т. е. , то 0,301 – изображение логарифма по основанию десять; 2 – оригинал.

Тем же методом пользуются при расчетах синусоидальных электрических цепей в символическом виде:

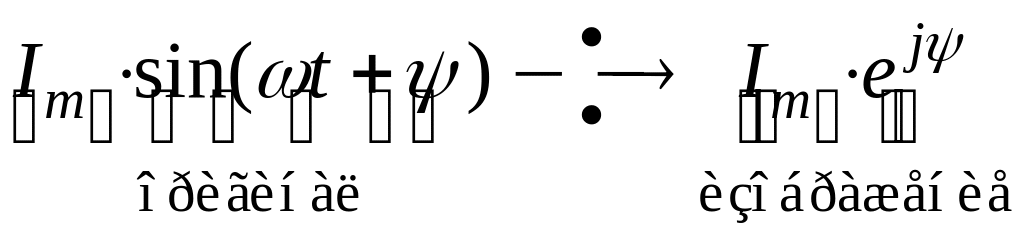
3.2.2. Преобразование Лапласа

Условимся под р понимать комплексное число:

.

Функцию времени (напряжение, ток, ЭДС, заряд) обозначают и называют оригиналом. Ей соответствует функция , называемая изображением и определяемая следующим образом:

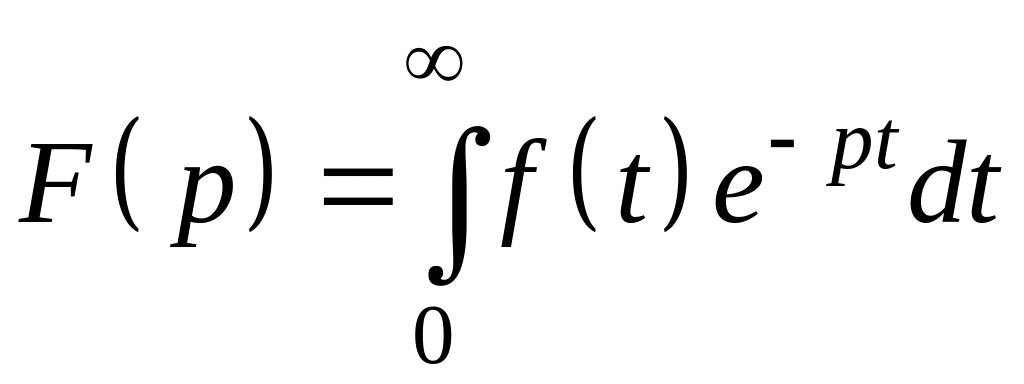. (3.13)

Соответствие между и записывают в виде:

,

где знак - называют знаком соответствия.

Верхний предел интеграла равен бесконечности, такой интеграл называют несобственным. Если в результате интегрирования получается конечное число, то говорят что интеграл сходится.

Сформулируем признак сходимости такого интеграла: если модуль функции с увеличением t увеличивается меньше, чем модуль функции , равный , то интеграл является сходящимся.

3.2.3. Определение операторного метода расчета

Операторный метод расчета основан на использовании понятия изображения функции времени. Переход от функции времени к функции осуществляется с помощью прямого преобразования Лапласа.

Операторный метод позволяет свести операцию дифференцирования к умножению, а операцию интегрирования к делению. Это облегчает решение дифференциальных уравнений.

3.2.4. Изображение постоянной

Найдем изображение функции , где А – постоянная величина.

.

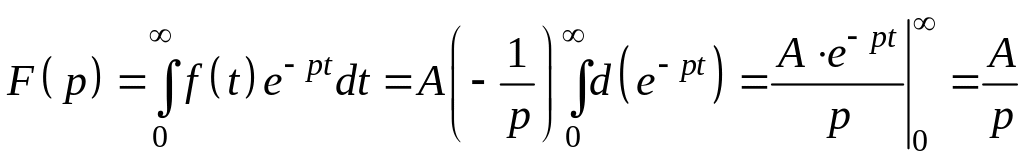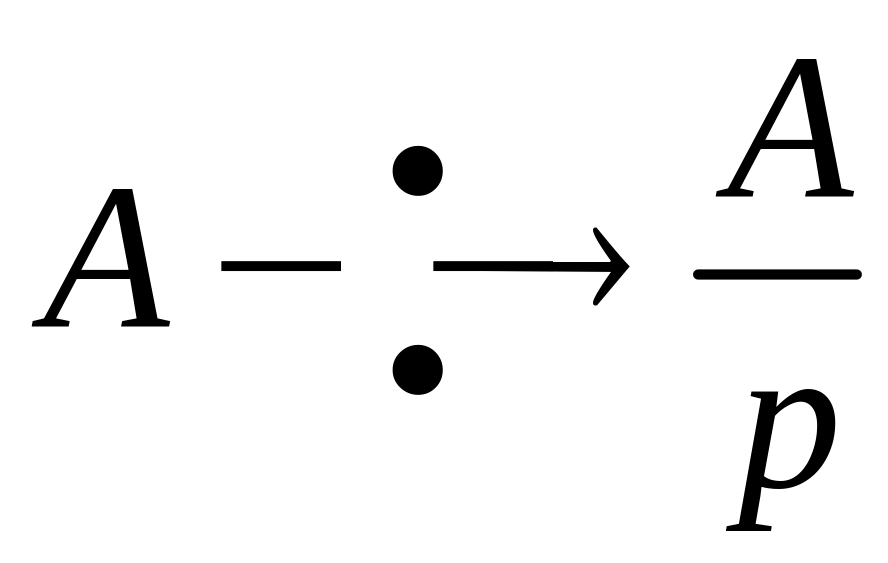. (3.14)

3.2.5. Изображение напряжения на индуктивности

Известно выражение:

.

После преобразования Лапласа производной будет соответствовать изображение:

, (3.15)

где значение тока в момент времени . Следовательно, после преобразования Лапласа напряжению на индуктивности будет соответствовать изображение:

. (3.16)

3.2.6. Изображение напряжения на конденсаторе

Напряжение на конденсаторе определяется выражением:

.

При подстановке пределов интегрирования выражение примет вид:

,

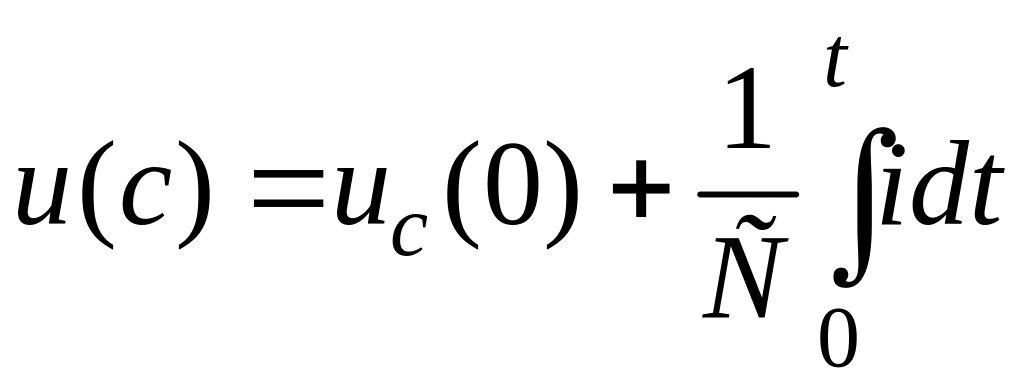где - напряжение на конденсаторе в момент времени .

Интегрируя по частям, получим:

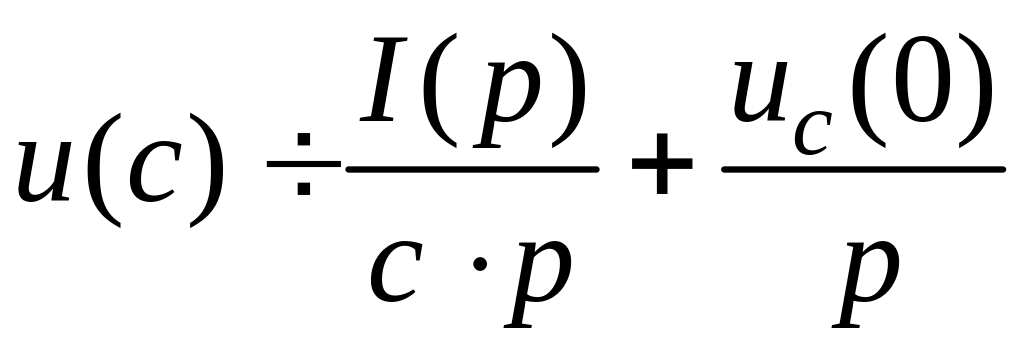. (3.17)

3.2.7. Закон Ома в операторной форме. Внутренняя эдс

Рассмотрим участок электрической цепи, имеющий активное, индуктивное и емкостное сопротивления R, L, C и источник ЭДС.

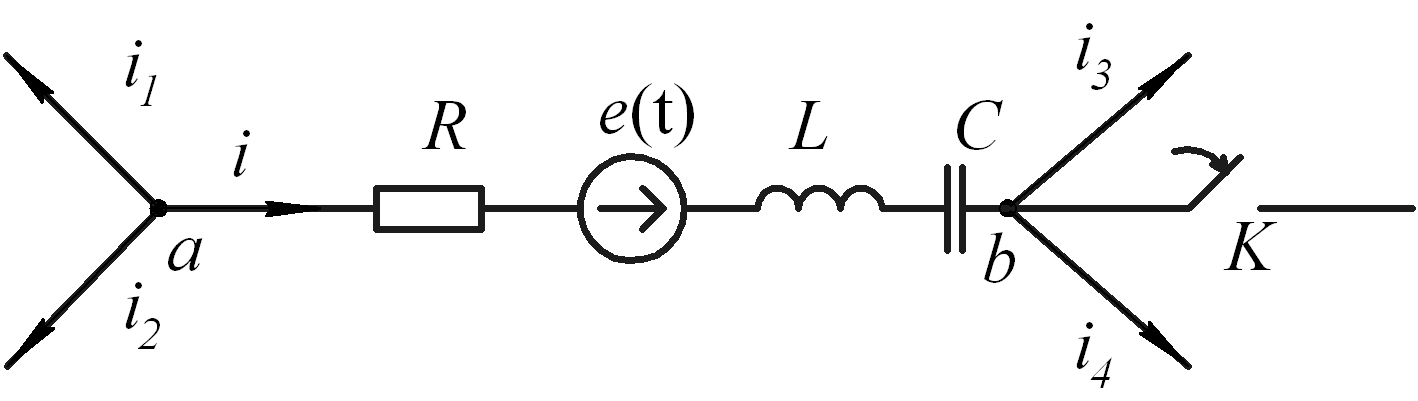
Рис. 3.8

Замыкание ключа К приводит к переходному процессу.

До коммутации были известны начальные значения в цепи и , которые являются независимыми. Пусть и .

Напряжение на участке определяется выражением:

.

Или в полном виде:

.

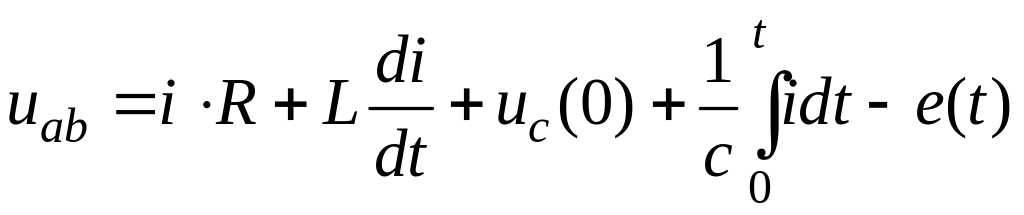Применив к полученному выражению преобразование Лапласа, получим:

, , ,

, .

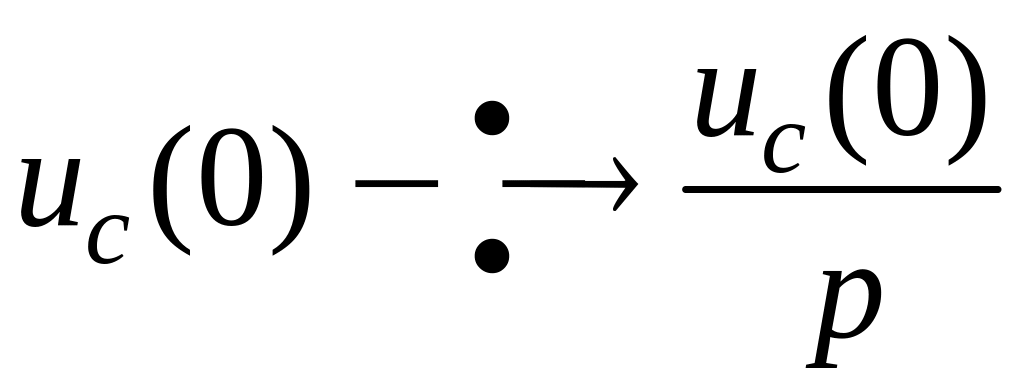В результате:

.

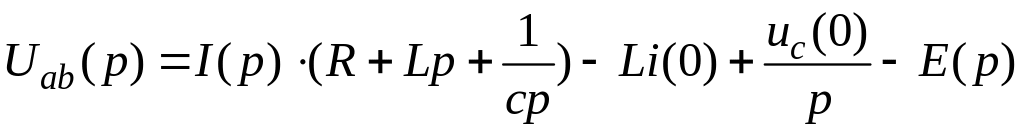Выразим :

,

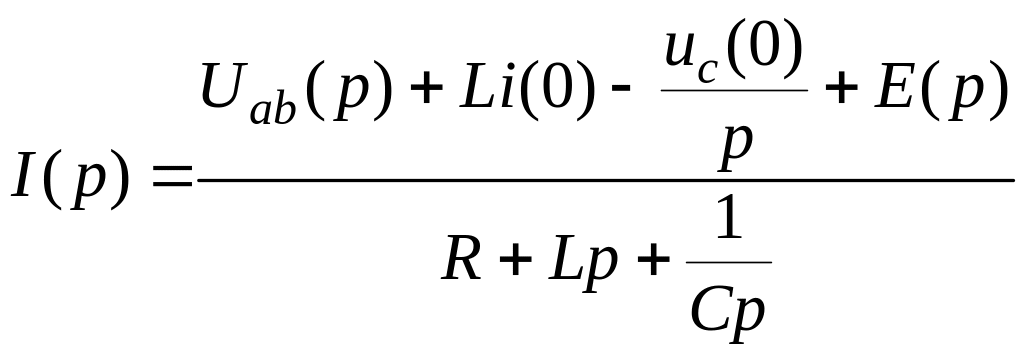где представляет собой операторное сопротивление участка . Его структура аналогична комплексному сопротивлению при замене на .

Тогда выражение для тока примет вид:

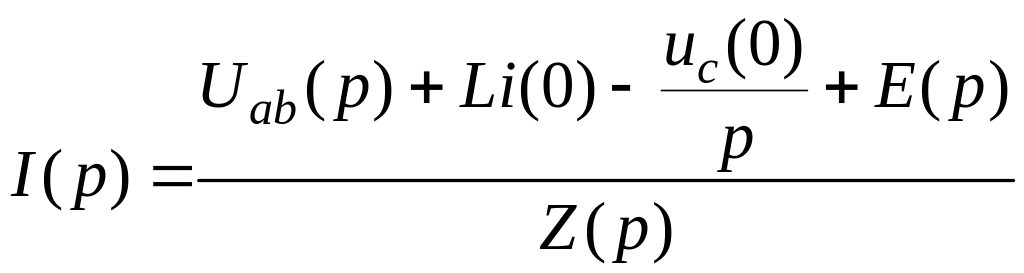(3.18)

Слагаемое представляет собой внутреннюю ЭДС, обусловленную запасом энергии в магнитном поле индуктивности, вследствие протекания через L до коммутации тока . Эта ЭДС направлена согласно с направлением тока .

Слагаемое представляет собой внутреннюю ЭДС, обусловленную запасом энергии в электрическом поле конденсатора вследствие наличия запаса заряда до коммутации при напряжении . Эта ЭДС направлена встречно .

Обозначим и 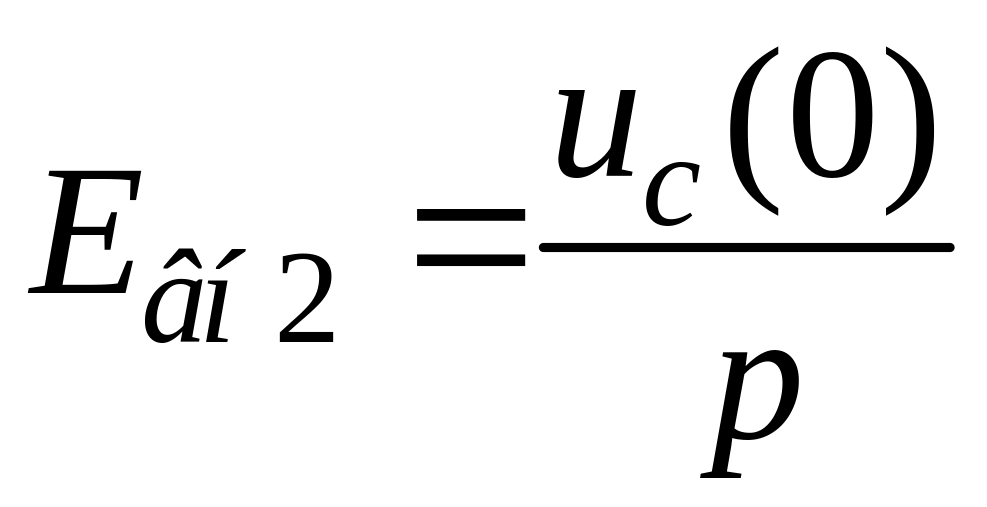, подставим в выражение (3.18) и получим:

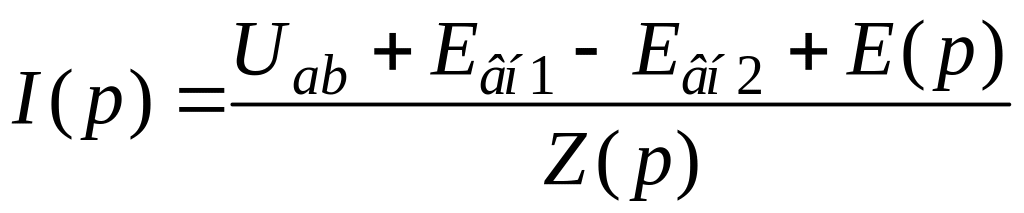. (3.19)

Это выражение называется законом Ома в операторной форме (для переходного процесса).