2.4.2. Последовательность исследования резонанса

1) Записывается входное сопротивление цепи (в случае резонанса напряжений) или входная проводимость (в случае резонанса токов).

2) Входное сопротивление (проводимость) представляется в алгебраической форме (разделяется на действительную и мнимую части).

3) Выделяется реактивное сопротивление (проводимость) цепи (мнимая часть) и приравнивается к нулю.

4) Полученное уравнение решается относительно искомой неизвестной (частоты, индуктивности, емкости, сопротивления).

Исследование явления резонанса в цепях, содержащих три и более реактивных элемента, имеет ту же основу, т.е. при резонансе входное сопротивление (проводимость) цепи становится чисто активным. Задача чаще всего сводится к определению резонансных частот и построению, если в том есть необходимость, частотных зависимостей реактивных сопротивлений (проводимостей) от частоты.

Рассмотрим конкретный пример. На рис. 2.21 изображена схема с тремя реактивными элементами.

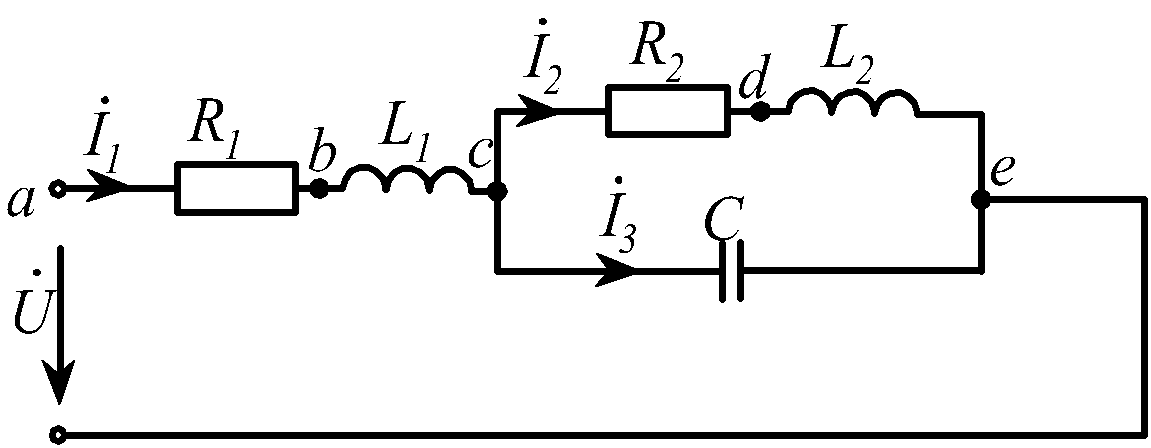
Рис. 2.21

Входное комплексное сопротивление имеет вид:

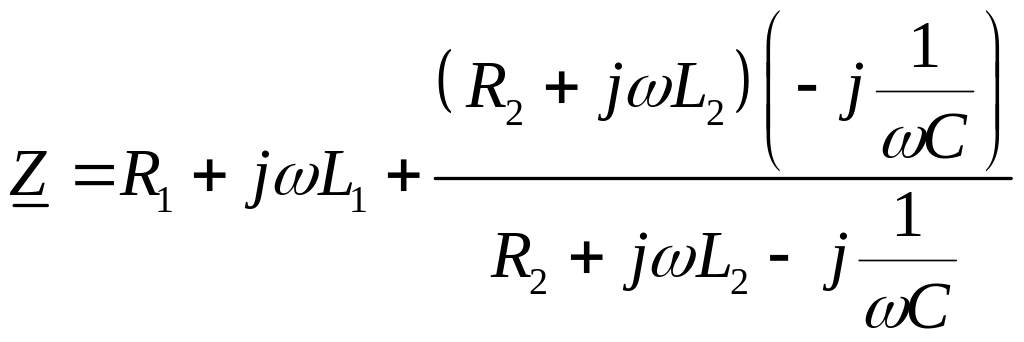. (2.4)

После разделения действительной и мнимой частей приходим к выражению:

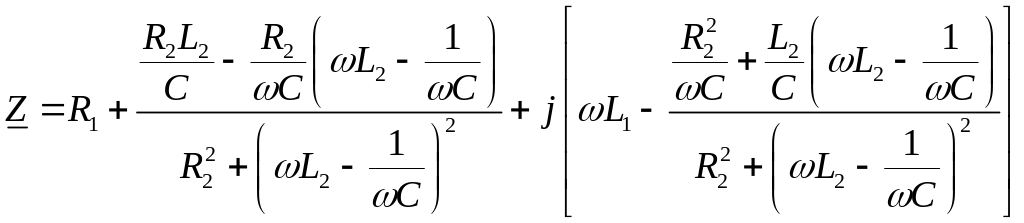. (2.5)

Далее используется только мнимая часть. Приравнивая к нулю и подставляя ω = ω₀, получаем уравнение

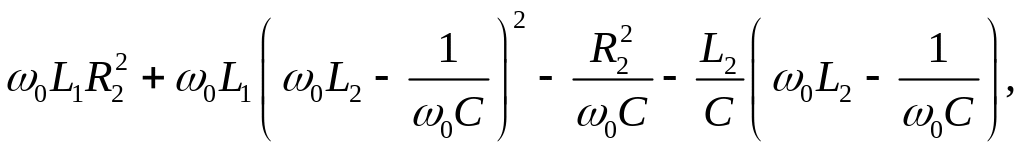(2.6)

корни которого определяют резонансные частоты.

Следует учитывать, что положительный ответ на вопрос о возможности возникновения того или иного резонанса дают только положительные действительные корни уравнения (2.6). Любые другие типы корней (отрицательные действительные, комплексные или мнимые) указывают на отсутствие резонанса в рассматриваемой схеме.

Например, при численных значениях параметров схемы рис. 2.21:

R₁ = 23 Ом, L₁ = 0,274 Гн, R₂ = 35 Ом, L₂ = 0,340 Гн, С = 20 мкФ

уравнение (2.6) приобретает вид:

,

тогда его корни будут иметь следующие значения:

ω₀₁ = ± 380 рад/с, ω₀₂ = ± 566 рад/с.

Из полученных корней два действительные, положительные, следовательно, можно сделать вывод о том, что в схеме наблюдаются резонансы при двух значениях частот:

ω₀₁ = 380 рад/с, ω₀₂ = 566 рад/с.

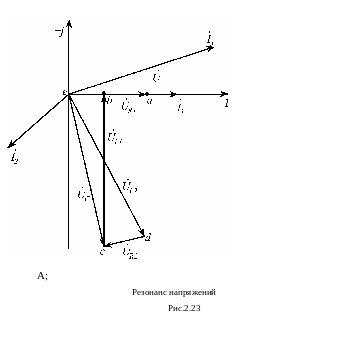
Чтобы ответить на вопрос о типе того или иного резонанса, необходимо дополнительно провести расчет режимов схемы при полученных резонансных частотах. На рис.2.22 и 2.23 представлены результаты расчета токов и векторные диаграммы, построенные в одном масштабе для схемы рис.2.21 при входном напряжении U = 2 В на частотах ω₀₁ = 380 рад/с и ω₀₂ = 566 рад/с.

При численных значениях параметров схемы рис. 2.29:

R₁ = 23 Ом, L₁ = 0,274 Гн, R₂ = 35 Ом, L₂ = 0,340 Гн, С = 1000 мкФ

уравнение (2.6) приобретает вид:

т огда его корни будут иметь следующие значения:

ω₀₁ = ± 61,7 рад/с, ω₀₂ = ± j70,1 рад/с.

что говорит о наличии одной резонансной частоты ω₀₁ = ± 61,7 рад/с.

Удобство использования комплексного сопротивления или проводимости определяется топологией схемы, а решение уравнений X = 0 или B = 0 приводит к одинаковым результатам.