2.3.3. Примеры расчета

Задача 1. В электрической цепи (рис. 2.15) заданы следующие параметры:

U = 5 B;	R1 = 2 Ом;	R2 = 2 Ом;	Ом;
= 3 Ом;	XС = 2 Ом;	XМ = 1 Ом.

Требуется:

а) комплексным методом определить ток цепи;

б) построить векторную топографическую диаграмму.

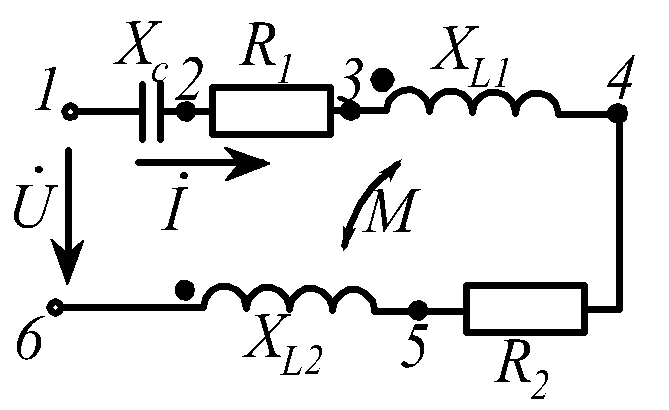
Рис. 2.15

Решение.

Расчетный ток входит в начало первой и конец второй катушки, следовательно, катушки включены встречно. По второму закону Кирхгофа имеем:

или

После подстановки и вычислений определяем комплексное действующее значение входного тока цепи

А.

Соответствующая векторная топографическая диаграмма приведена на рис. 2.16.

П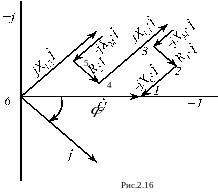 ояснения к диаграмме.

Напряжение между точками 5 и 6 схемы соответствует разности напряжений, созданных во второй катушке явлениями само- и взаимоиндукции, т.е.

По аналогии

Кроме того,

З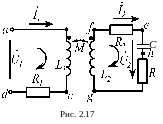 адача 2. К первичной обмотке трансформатора без стального сердечника (рис. 2.17) подведено напряжение

= 120 В.

Параметры схемы: R₁ = 10 Ом, ωL₁ = 42 Ом, R₂ = 15 Ом, ωl₂ = 70 Ом, R = 5 Ом, = 10 Ом, ωm= 20 Ом.

Требуется:

а) определить напряжение на нагрузке ;

б) построить векторную диаграмму напряжений в каждом контуре схемы.

Решение.

Напряжение на нагрузке RС можно вычислить, предварительно определив токи и . С этой целью составим два уравнения по второму закону Кирхгофа, направив обходы контуров по токам.

Сравнивая направления токов относительно одноименных зажимов, делаем вывод, что включение катушек встречное, поэтому падения напряжения взаимной индукции отрицательные:

Упростим эти выражения, обозначив собственные сопротивления контуров и , взаимное сопротивление :

тогда полученная система уравнений

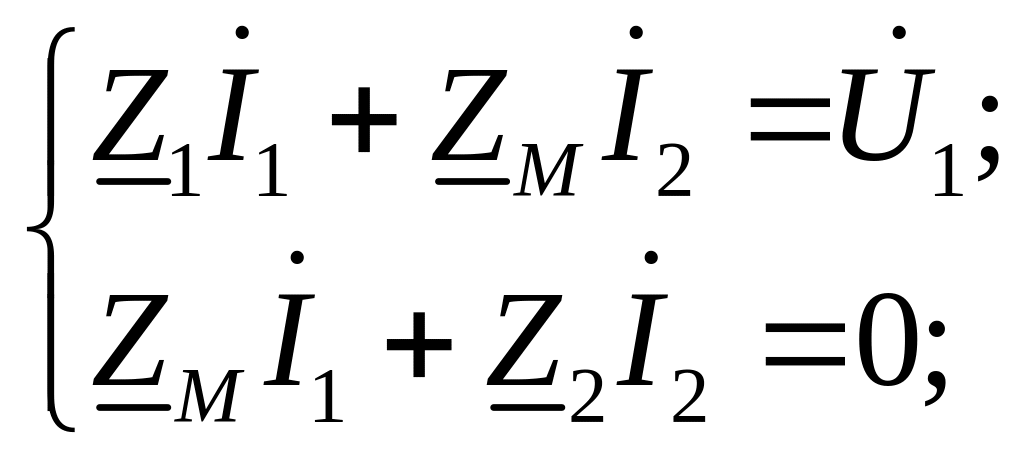
внешне совпадает с системой, записанной по методу контурных токов для данной схемы.

После подстановки и расчетов получаем:

А; А;

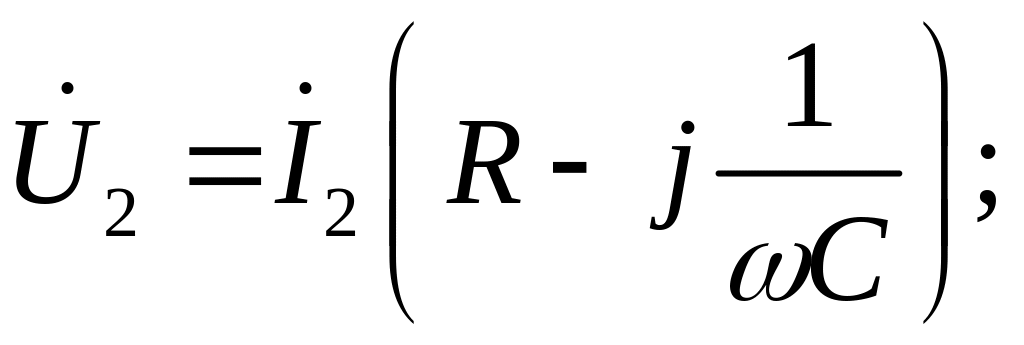
В.

П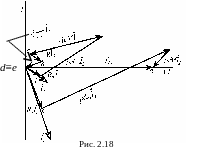 остроение векторной диаграммы (рис. 2.18) начинаем с проведения векторов токов и . Затем из начала координат по направлению вектора откладываем в масштабе вектор падения напряжения и под углом +90° - вектор . Поскольку включение катушек встречное, то вектор падения напряжения в катушке L₁ от тока отстает от вектора этого тока на угол 90°. Суммирующим является вектор входного напряжения . Аналогично строится векторная диаграмма падений напряжения во втором контуре, где вектор отстает на 90° от вектора тока . Сумма векторов равна нулю.

2.4. Резонансы в электрических цепях

2.4.1. Сведения из теории

Признаком резонанса в электрической цепи, содержащей индуктивности и емкости, является совпадение по фазе напряжения и тока на ее входе.

При последовательном соединении индуктивности и емкости (рис.2.19,а) или при последовательном соединении участков, содержащих индуктивность и емкость (рис.2.19,б-г), возможен резонанс напряжений.

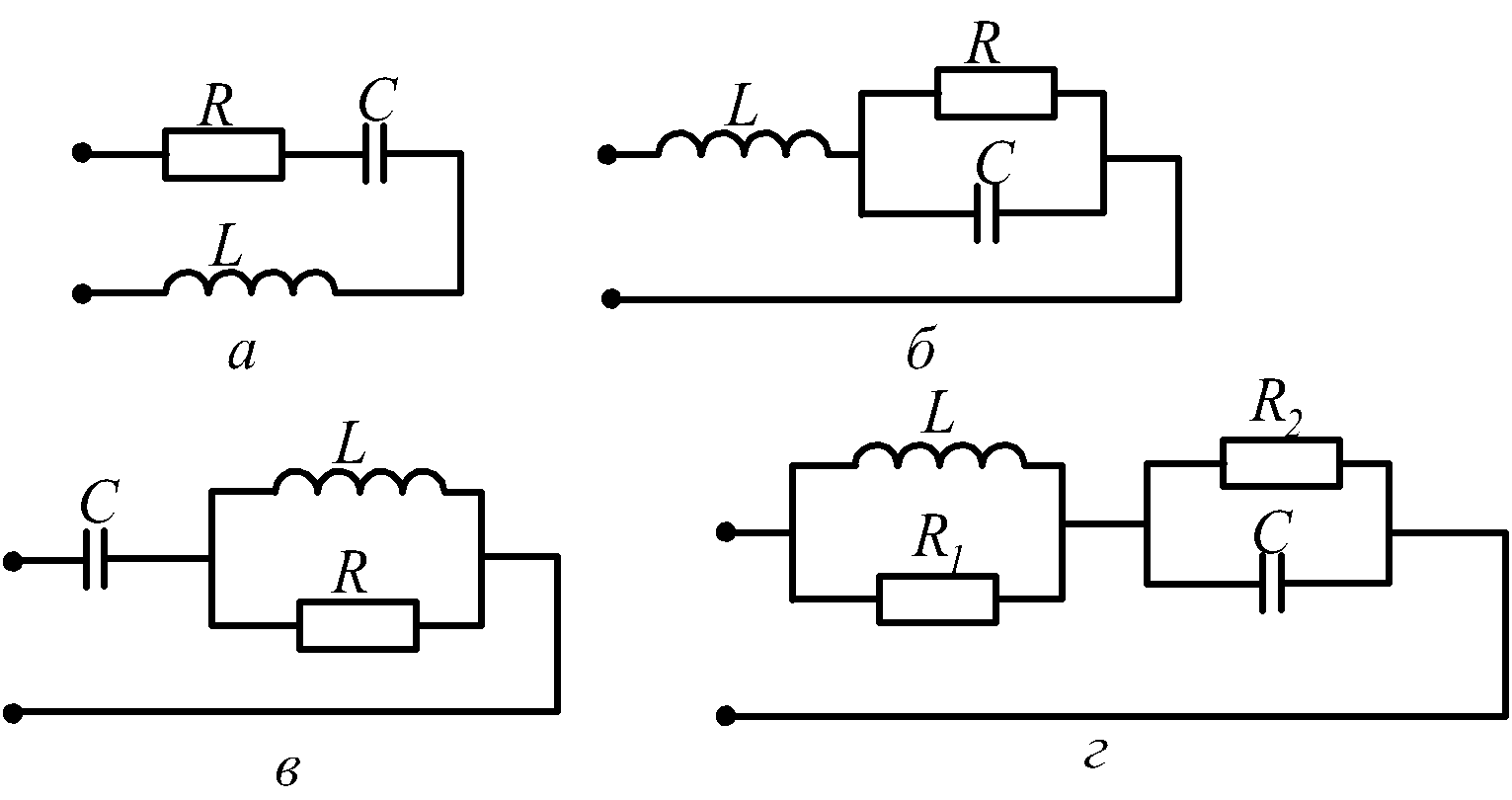
Рис. 2.27

При резонансе напряжений индуктивное сопротивление цепи компенсируется емкостным, в результате входные реактивные сопротивление и мощность равны нулю, напряжения на реактивных элементах могут значительно превышать входное.

При параллельном соединении индуктивности и емкости (рис.2.20,а) или при параллельном соединении участков, содержащих индуктивность и емкость (рис. 2.20,б-г), возможен резонанс токов.

При резонансе токов индуктивная проводимость цепи компенсируется емкостной, в результате реактивная проводимость и реактивная мощность на входе цепи равны нулю, токи в реактивных элементах могут значительно превышать входной ток.

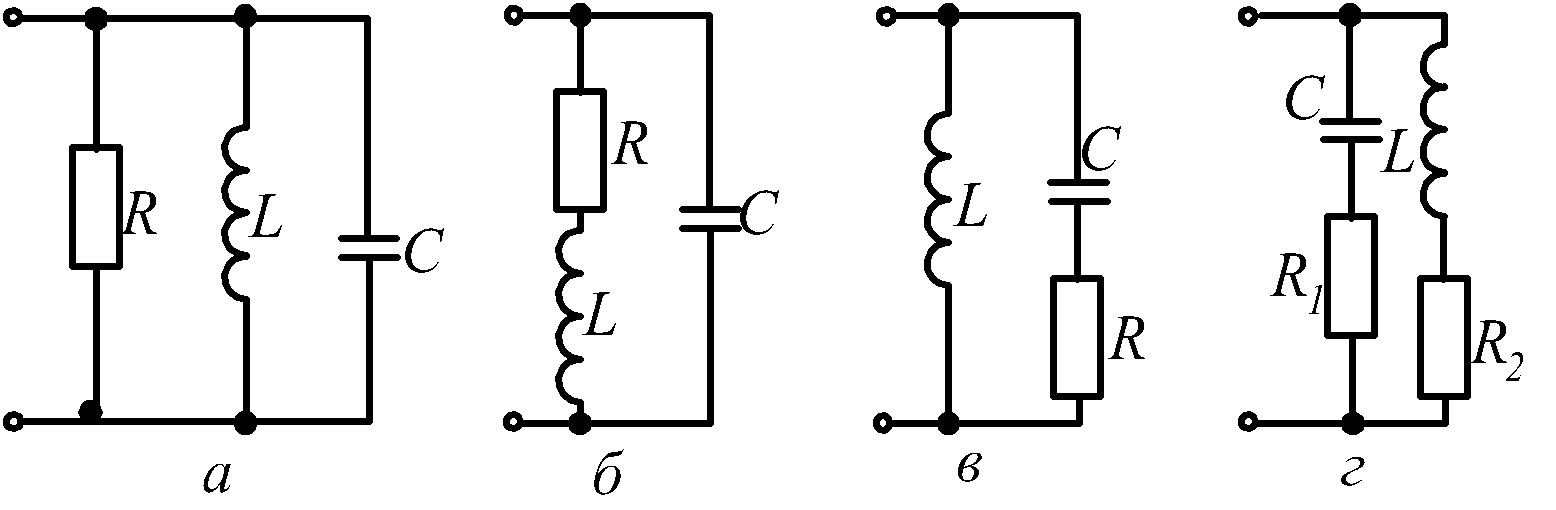
Рис. 2.20

Частота, при которой наблюдается резонанс, называется резонансной. При исследовании резонансных режимов обычно определяется резонансная частота, значения индуктивности или емкости, при которых на заданной частоте возникает резонанс, а также рассчитываются частотные характеристики – зависимости токов, напряжений, сопротивлений, проводимостей от частоты.