Лекция 9. Эйлеровы пути

Первая теорема теории графов (Леонард Эйлер, 1736 год)

ЭЙЛЕРОВЫМ ПУТЕМ в графе называется произвольный путь, проходящий через КАЖДОЕ ребро в точности ОДИН раз.

Если путь заканчивается в начальной вершине, то он называется ЭЙЛЕРОВЫМ ЦИКЛОМ.

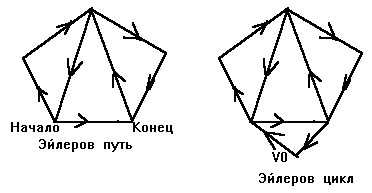
Рис. 22

Задача существования эйлерова пути в заданном графе была решена великим русским математиком ЛЕОНАРДОМ ЭЙЛЕРОМ в 1736 году.

Представленное им необходимое и достаточное условие существования такого пути считается первой в истории математики теоремой теории графов.

ТЕОРЕМА.

Эйлеров путь существует тогда и только тогда, когда граф связный и содержит не более ДВУХ ВЕРШИН НЕЧЕТНОЙ СТЕПЕНИ. (Напомним,степень вершины — число смежных с нею ребер).

Заметим, что число вершин нечетной степени в любом графе всегда ЧЕТНО. Это легко доказать.

Просуммируем степени всех вершин графа. Эта сумма равна 2*m — удвоенному числу ребер, т.к. каждое ребро соединяет две вершины. Вклад в эту сумму вершин четной степени — четен, поэтому вклад вершин нечетной степени тоже должен быть четен. Для этого их должно быть четное количество (нечетное число ребер * четное число вершин = четный результат).

Новая формулировка теоремы:

ЭЙЛЕРОВ ПУТЬ В СВЯЗНОМ ГРАФЕ СУЩЕСТВУЕТ ТОГДА И ТОЛЬКО ТОГДА, ЕСЛИ ЧИСЛО ВЕРШИН НЕЧЕТНОЙ СТЕПЕНИ РАВНО 0 ИЛИ 2.

Докажем достаточность.

Если эйлеров путь существует, то нечетную степень имеют ровно две вершины — начало и конец. Если это цикл, то таких вершин — 0.

В дальнешем будем рассматривать только эйлеровы циклы u, соответственно, графы без вершин нечетной степени. Если граф имеет 2 «нечетных» вершины, то добавим еще одну вершину и соединим ее ребрами с нечетными (см. рисунок 22). «Нечетные» вершины станут четными, эйлеров путь замкнется в цикл.

Поэтому необходимое условие сформулируем только для циклов:

ЕСЛИ В СВЯЗНОМ ГРАФЕ НЕТ ВЕРШИН НЕЧЕТНОЙ СТЕПЕНИ, В НЕМ СУЩЕСТВУЕТ ЭЙЛЕРОВ ЦИКЛ.

Доказательство необходимости будет следовать из анализа алгоритма его нахождения.

?Вопрос 1. Существует ли эйлеров цикл в данном графе :

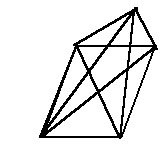
Рис. 23

АЛГОРИТМ. {Нахождение эйлерова цикла}

Данные: Связный граф G = <V, E> без вершин нечетной степени, представленный списками инцидентности ЗАПИСЬ[v], v  V.

Результаты: Эйлеров цикл, хранящийся в стеке EC.

1 begin

2 СТЕК:=NIL; EC:=NIL;

3 k := произвольная вершина G;

4 СТЕК<= k; {поместим k в СТЕК}

5 while СТЕК <> NIL do

6 begin

7 v:=top(CTEK); {верхний элемент СТЕКА}

8 if ЗАПИСЬ[v]<>0 then {ищем ребро, выходящее из v}

9 begin

10 u:= первая вершина списка ЗАПИСЬ[v];

11 СТЕК <= u; {поместим u в СТЕК}

12 ЗАПИСЬ[v]:=ЗАПИСЬ[v] - [u];

13 ЗАПИСЬ[u]:=ЗАПИСЬ[u] - [v]; {удаляем ребро (v-u) из графа G}

14 end {возврат на 5, теперь u — верхнии элемент}

15 else {из v не выходит ни одно ребро, путь нельзя удлинить}

16 begin

17 v <= СТЕК; ЕС <= v {v выталкивается из СТЕКА и помещается в ЕС}

18 end

19 end {пока СТЕК не пуст}

20 end.

Пусть k — вершина, выбранная в 3.

Цикл 5 начинает строить путь с началом в k, вершины этого пути помещаются в СТЕК, ребра удаляются из графа. Это продолжается до тех пор, пока не выполнится ЗАПИСЬ[v ]= 0 в 15.

Это означает, что путь нельзя удлинить, он кончился на v. На самом деле v = k, т.к.иначе степень v была бы нечетной — зашли в v, но не вышли. Таким образом, мы вышли из k и вернулись в k т.е. описали цикл. Его вершины находятся в СТЕКЕ, ребра удалены из графа. Вершина k переносится из СТЕКА В ЕС, а «очередной» вершиной v становится верхний элемент СТЕКА.

Процесс повторяется, в СТЕК помещается некоторый цикл, проходящий через v, сама v переноситься в ЕС. По окончании работы СТЕК пуст, ЕС содержит эйлеров цикл.

На рис. 24 изображен «модельный» граф, на котором удобно продемонстрировать работу алгоритма. Направления стрелок указывают, в какой последовательности ребра графа G попадают в стек ЕС.

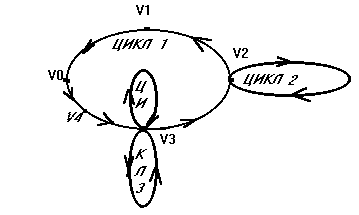
Рис. 24

Вначале в СТЕК помещается цикл 1 (V₀—V₁—V₂—V₃—V₄—V₀), он удаляется из графа, V₀ заносится в ЕС.

Затем из СТЕКА удаляется верхний элемент V₄. Все проходящие через него ребра удалены из графа, V₄ переносится в ЕС.

Затем в СТЕК помещается цикл 3, V₃ из СТЕКА переносится в ЕС.

Затем из СТЕКА в ЕС переносятся все элементы цикла 3, т.к. проходящие через них ребра удалены. Следующий верхний элемент — V₂ и т.д.

Оценим вычислительную сложность алгоритма.

Главный цикл 5 работает, пока СТЕК не пуст. Каждое ребро графа один раз записывается в СТЕК и один раз переносится в ЕС. Число итераций цикла 5 — О(m). Покажем что число шагов внутри каждой итерации ограничено константой. Одна итерация или записывает ребро в СТЕК, удаляя его из графа, или переносит в ЕС. Списки инцидентности ЗАПИСЬ[v] реализованы так, что для вершин u—v, соединенных ребром, вершина u в списке ЗАПИСЬ[v] содержит указатель на вершину v в списке ЗАПИСЬ[u] и наоборот. Это позволяет удалить ребро (v—u) за время, ограниченное константой. Построенный алгоритм является оптимальным, т.к. только выписывание эйлерова цикла потребует О(m) шагов.

Ответы

Ответ 1. Вначале обходим стороны пятиугольника,образуя цикл, затем «одним росчерком пера» пробегаем звездочку.