Лекция 5. Поиск в ширину в графе

Бросая в воду камни, следи за кругами, ими образуемыми; иначе такое занятие будет пустою забавою. Козьма Прутков «Мысли и афоризмы»

При ПОИСКЕ В ГЛУБИНУ просмотренные, но еще не использованные вершины скапливались в стеке. Чем позднее была просмотрена вершина, тем раньше ее удаляли из стека. Заменим стек ОЧЕРЕДЬЮ.

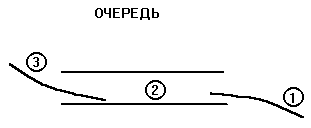
Рис. 11

Механизм подключения элемента к началу очереди полностью совпадает с вталкиванием в стек (процедура push). Механизм ВЫТАЛКИВАНИИЯ ИЗ ОЧЕРЕДИ (функции poptail) — первым из очереди удаляется первый попавший туда элемент.

Основная идея ПОИСКА В ШИРИНУ — у вершины v просматриваются и помещаются в очередь СРАЗУ ВСЕ ее новые «соседи», после чего v становится использованной и удаляется из очереди.

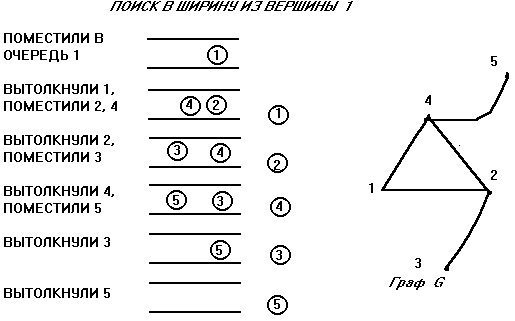
Рис. 12

Поиск в ширину можно использовать для нахождения КРАТЧАЙШЕГО пути между парой фиксированных вершин s и t. Так как мы находим сразу всех соседей, поиск, как волна от источника, равномерно распространяется во все стороны. Поэтому в очереди сначала находятся все вершины, удаленные от s на расстояние 1, через некоторое время — все вершины, удаленные на расстояние 2 и т.д. Понятно, что путь, найденный таким образом, будет кратчайшим.

Рис. 13

Процедура поиска в ширину SH:

1 procedure SH(v);

{поиск в ширину с началом в вершине v}

2 begin

3 ОЧЕРЕДЬ:=NIL; ОЧЕРЕДЬ<= v; НОВЫЙ[v]:=ложь;

{v помещается в очередь}

4 while ОЧЕРЕДЬ<>NIL do

5 begin

6 tail <=ОЧЕРЕДЬ;

{выталкивание из очереди нижнего элемента}

7 for u ЗАПИСЬ[tail] do

{ищем ВСЕХ новых соседей узла tail}

8 if НОВЫЙ[u] then

9 begin

10 ОЧЕРЕДЬ <= u; НОВЫЙ[u]:=ложь

11 end

12 end {while ОЧЕРЕДЬ <>NIL}

13 end;

Как и для поиска в глубину, легко показать, что каждая вершина просматривается ровно один раз и вычислительная сложность равна O(n+m).

Чтобы найти кратчайший путь, нужно немного модифицировать процедуру SH. Во-первых, добавить одномерный массив ПРЕД по числу вершин графа. Пусть во время работы процедуры в вершину u₂ мы попали из u₁: u₁ была предыдущей для u₂, поэтому ПРЕД[u₂]:=u₁. Во-вторых, чтобы массив ПРЕД заполнялся именно так, изменим строку 10 процедуры SH:

9 begin

10 ОЧЕРЕДЬ<=u; НОВЫЙ[u]:=ложь;

ПРЕД[u]:=tail;

Итак, чтобы найти кратчайший путь из s в t, вызовем модифицированную SH(s).

Как только конец пути t попадет в очередь, поиск следует прекратить. Каким образом извлечь путь от s до t из массива ПРЕД?

Рассмотрим последовательность вершин, где u₁=ПРЕД[u₂]. В t мы попали из u, в u из v и т.д., пока не встретим s. Эта последовательность — путь из s в t. Первоначальная инициализация массива ПРЕД: ПРЕД[u]:=u.

?Вопрос 1. Как будет заполнен массив ПРЕД при поиске в ширину на рис. 12 в момент помещения в очередь вершины 5?

Метод поиска в ширину применим для определения связных компонент графа. Вызвав SH(s), просмотрим все вершины u, для которых существует путь из s в u.

Ответы.

Ответ 1. ПРЕД[1]=1; ПРЕД[2]=ПРЕД[3]=1; ПРЕД[4]=3; ПРЕД[5]=2.

Лекция 6. Стягивающие деревья (кАркасы)

У моря есть морская рыбка, Скрипичный ключ имеет скрипка… У. Дж. Смит «У моря есть морская рыбка…»

Каждый связный граф имеет каркас. Более того, у одного графа может быть несколько разных каркасов. Дадим теперь определение каркаса.

Дерево — произвольный неориентированный связный граф без циклов.

Для произвольного связного графа G=<V, E> любое дерево D=<V, T>, где T Í Е будет его КАРКАСОМ.

Другими словами, каркас D соединяет ВСЕ вершины графа G так, чтобы не было циклов.

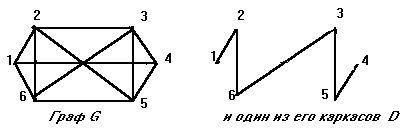
Рис. 14

Ребра КАРКАСА будут называться ВЕТВЯМИ, ребра, не вошедшие в каркас, ХОРДАМИ.

?Вопрос 1. Перечислите хорды графа G относительно каркаса D на рис. 14.

Каркасы можно строить как поиском в глубину, так и поиском в ширину. В обоих случаях достижение новой вершины u из старой v означает включение в каркас ветви (v-u).

АЛГОРИТМ {Нахождение каркаса связного графа методом поиска в глубину}

Данные: Связный граф G <V, E>, заданный списками инцидентности ЗАПИСЬ[v], v V.

Результаты: Каркас D = <V, T> графа.

Переменные НОВЫЙ, ЗАПИСЬ, Т — глобальные

1 procedure GLD(v);

2 begin

3 НОВЫЙ[v]=ложь;

4 for u ЗАПИСЬ[v] do

5 if НОВЫЙ[u] then {нашли новую ветвь (v — u)}

6 begin

7 T:= T  (v-u); {и присоединили ее к множеству 8 ветвей каркаса}

9 GLD(u)

10 end

11 end; {конец процедуры GLD(v)}

1 begin {основная программа}

2 for u V do НОВЫЙ[u]:=истина; {инициализация}

3 T:=0; {T-множество найденных ветвей}

4 GLD(k) {корень k — произвольная вершина}

5 end.

Докажем корректность этого алгоритма.

Алгоритм строит СВЯЗНЫЙ граф, т.к. каждое новое ребро (v-u) продолжает уже существующий путь от k к v.

Построенный граф не содержит ЦИКЛОВ. Каждая новая ветвь (v-u) соединяет уже рассмотренную v с НОВОЙ u. Чтобы замкнуть цикл, требуется ребро, соединяющее две уже РАССМОТРЕННЫЕ вершины.

Построенный граф содержит ВСЕ вершины графа G — это свойство поиска в глубину. По этой же причине вычислительная сложность алгоритма О(n+m).

Любой каркас обладает важным свойством — от корня k до произвольной вершины v существует ровно ОДИН путь, состоящий из ветвей каркаса. Если бы их было два, получился бы цикл, если бы ни одного, каркас не был бы связным.

Кроме того, если каркас D построен поиском в глубину, то для двух вершин u и v, СОЕДИНЕННЫХ РЕБРОМ e E, всегда можно сказать: или v — потомок u, или u — потомок v (относительно каркаса D).

Первое означает, что u лежит на пути из корня k в вершину v, второе — v на пути из k в u. Это легко доказать.

Пусть одна из вершин, например,v просмотрена раньше u. Построен путь от корня k до v. Процесс поиска в глубину начинается с вершины v. Так как u и v соединены ребром, то, рано или поздно, будет рассмотрена вершина u и построен путь от v до u. Получился путь k—v—u.

Если v и u соединены ВЕТВЬЮ каркаса, то одна из них — СЫН, другая — ОТЕЦ.

АЛГОРИТМ {Каркас связного графа ПОИСКОМ В ШИРИНУ}

Данные: связный граф G=<V, E>, представленный списками ЗАПИСЬ[v], v   V.

Результаты: каркас D = <V, T> графа G.

1 begin

2 for u V do НОВЫЙ[u]:=истина; {инициализация}

3 T:=0 {T — множество найденных ветвей}

4 ОЧЕРЕДЬ=NIL; ОЧЕРЕДЬ <= k;

5 НОВЫЙ[k]:=ложь; {k — корень}

6 while ОЧЕРЕДЬ <> NIL do

7 begin v<= ОЧЕРЕДЬ; {вытолкнули из очереди нижний элемент}

8 for u ЗАПИСЬ[v] do

9 if НОВЫЙ[u] then {нашли новую ветвь v—u}

10 begin

11 ОЧЕРЕДЬ <=u; НОВЫЙ[u]:=ложь;

12 T:=T (v-u) {и присоединили ее к каркасу}

13 end

14 end

15 end.

Легко доказать, что этот алгоритм строит каркас произвольного графа за О(n+m) шагов.

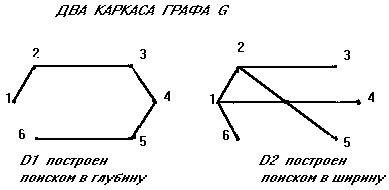
Рис. 15

Если каркас D графа G построен ПОИСКОМ В ШИРИНУ, то путь от корня k до произвольной вершины v будет не только единственным, но и КРАТЧАЙШИМ. Это следует из свойств поиска в ширину.

Ответы.

Ответ 1. {(2—3), (3—4), (5—6), (6—1), (2—5), (1—4)}.