Лекция 16. Пути в бесконтурном графе

Для бесконтурного графа с произвольными весами дуг задача нахождения кратчайшего пути может быть решена за О(m) шагов. Рассмотрим модельный бесконтурный граф (рис. 32).

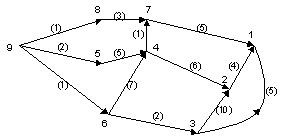
Рис. 32

Любой бесконтурный граф обладает следующим свойством:

его вершины можно перенумеровать так, что любая дуга будет идти от вершины с меньшим номером к вершине с большим номером.

Такую нумерацию будем называть правильной. Для нашего модельного графа пример возможной правильной нумерации приведен на рис. 33.

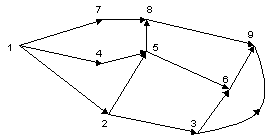
Рис. 33

Доказательством этого свойства будет служить алгоритм 4.

Алгоритм основывается на следующем простом факте:

в бесконтурном графе существует хотя бы одна вершина, в которую не заходит ни одна дуга (иначе бы в графе существовал контур).

Все такие вершины соберем в СТЕК. Затем

1) вытолкнем из СТЕКА произвольную вершину,

2) присвоим ей номер 1,

3) удалим ее из графа вместе со всеми выходящими из нее дугами.

После операции удаления дуг могут появиться новые вершины, в которые не заходит ни одна дуга. Эти вершины помещаются в СТЕК, затем из СТЕКА выталкивается произвольная вершина, ей присваивается следующий номер и т.д.

Понятно, что в результате получится правильная нумерация, так как любая вершина u получает номер в тот момент, когда оставшиеся еще незанумерованные вершины v (позже они получат большие номера ) либо не соединены дугами с u, либо дуга идет в направлении u→v.

Не так очевидно, почему все вершины получат номера:

если из СТЕКА удалили последнюю вершину, а в графе, получившемся после удаления этой вершины и выходящих из нее дуг, все вершины имеют заходящие в них дуги, то они уже никогда не попадут в СТЕК и никогда не получат номера.

Дело в том, что при удалении из бесконтурного графа вершин и дуг всегда получается бесконтурный граф, а в нем существует хотя бы одна вершина без заходящих в нее дуг. Поэтому каждая вершина обязательно попадет в СТЕК и получит соответствующий номер.

Поскольку из СТЕКА выталкивается произвольная вершина, то принцип стека не является обязательным и выбран только для удобства.

Алгоритм. {Правильная нумерация}

Данные: Бесконтурный орграф G=<V,E>, заданный списками инцидентности SLED[v], vV.

Результаты: Для каждой вершины v новый номер NN[v] такой, что номера NN[v] являются правильной нумерацией графа G.

1 begin

{INP[v] — число дуг, заходящих в вершину v}

2 for vV do INP[v]:=0;

3 for uV do

4 for v SLED[u] do

{находим все вершины v, дл я которых u→v}

5 INP[v]:=INP[v] + 1;

6 СТЕК:=0;

7 for vV do

8 if INP[v]=0 then СТЕК  v;

9 num:=0; {текущий номер}

10 while СТЕК <> 0 do

11 begin

12 u  СТЕК;

13 num:=num+1;

14 NN[u]:=num;

15 for v SLED[u] do

16 begin

17 INP[v]:=INP[v] — 1;

18 if INP[v]=0 then СТЕК  v;

19 end;

20 end;

21 end.

Все дуги графа анализируются два раза: в цикле 3-5 для подсчета числа заходящих дуг INP[v], в цикле 10-20, где удаление дуг из графа заменено уменьшением чисел INP[v].

Таким образом, вычислительная сложность алгоритма пропорциональна числу дуг, т.е. равна О(m) шагов.

Теперь можно считать, что у нас имеется бесконтурный граф с правильной нумерацией вершин, и вершина источник имеет номер 1.

Так как все дуги идут из вершины с меньшим номером в вершину с большим номером, то промежуточные вершины на пути от 1 до j будут иметь номера меньшие j. Поэтому для нахождения кратчайшего расстояния D[j] нужно знать только D[2],…,D[j-1]. Идея алгоритма следующая: зная D[1] (оно равно 0), вычислить D[2]; зная D[1] и D[2] вычислить D[3] и т.д.

Алгоритм. { Расстояния в бесконтурном графе }

Данные: Орграф G=<V,E> с правильной нумерацией, заданный списками PRED[v], матрица весов A[u,v], u,vV.

Результаты: Расстояния D[v] от источника 1 до всех остальных vV.

1 begin

2 D[1]:=0;

3 for j:=2 to n do D[j]:= ;

4 for j:=2 to n do

5 for i PRED[j] do

6 D[j]:= min( D[j], D[i] + A[i,j] );

7 end.

В цикле 4-6 каждая дуга анализируется ровно один раз, поэтому вычислительная сложность алгоритма равна О(m) шагов.

Бесконтурный граф может служить математической моделью для задач управления выполнением проектов. Дуги графа соответствуют элементарным задачам, состовляющим проект, веса дуг — времени, необходимому для выполнения элементарной задачи. Вершина s соответствует началу выполнения проекта, вершина t — его завершению. Для любых двух дуг u→v и v→p предполагается, что задача u→v должна быть закончена до начала выполнения задачи v→p. Самый длинный путь от s до t соответствует времени, минимально необходимому для выполнения всего проекта.

?Вопрос 4. Каким образом можно воспользоваться процедурой поиска крачайшего пути для нахождения самого длинного пути?