Лабораторная работа № 5 исследование системы трехфазного тока при соединений потребителей "звездой"

Цель работы:

Проверить опытным путём соотношение между фазными и линейны­ми напряжениями. Уяснить роль нулевого провода. Научиться строить векторные диаграммы напряжений и токов трехфазных цепей. Проана­лизировать с помощью векторных диаграмм изменение фазных напря­жений при наличии и отсутствии нулевого провода.

Основные теоретические положения

В цепях трехфазного тока всегда действует симметричная сис­тема трехфазной э.д.с. Независимо от способа соединения обмоток генератора систему напряжений, им вырабатываемых, можно предста­вить векторной диаграммой (рис.1). Если пренебречь сопротивлени­ем проводов линии и потерями нап­ряжений в ней, можно считать, что непосредственно на потребители воздействует эта же симметричная система линейных напряжений. Ре­жимы работы потребителей сущест­венно зависят от способа их соеди- нения и характера самих потребителей.

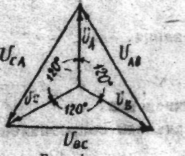
Рис 1.

1.Соединение потребителей "звездой" с нулевым проводом.

Электрическая цепь представлена на рис.2.

Рис.2

При наличии нулевого провода фазные напряжения на потребителе остается неизменными и равными фазным напряжениям генерато­ра.

UА = U’А, UВ = U’В, UС = U’С при любых видах нагрузки.

Измерив фазные и линейные напряжения на потребителях и ли­нейные токи (Iл = Iф ) помощью векторных диаграмм можно прове­рить выполнение первого закона Кирхгофа в трехфазных цепях:

Построение векторных диаграмм проводится следующим образом. Строится симметричная система фазных и линейных напряжений (см. рис.1). Поскольку потребители, используемые в работе, является активными, фазные токи откладывается в масштабе по направление фазных напряжений. Затем находится их векторная сумма. Результи­рующий вектор должен в масштабе соответствовать измеренному то­ку I₀ . Принцип построения остается неизменным во всех вариан­тах нагрузки.

Симметричной в трехфазной системе считается такая нагрузка, при которой, потребители трех фаз является одинаковыми по харак­теру и по величине, т.е.

ZА=ZВ=ZС; φА=φв=φС

Если хотя бы одно из этих условий не соблюдается, нагрузка яв­ляется несимметричной.

Пример построения векторной диаграммы для несимметричной нагрузки представлен на рис.3.

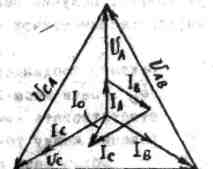
Рис.3

2. Соединение потребителей "звездой" в трехпроводной системе.

При симметричной нагрузке в четырехпроводной линии ток в нулевом проводе отсутствует. Если этот провод отсоединить,

ре­жим работы потребителей не изменится. Фазные напряжения на пот­ребителях U_A', U_B' , U_C' останутся одинаковыми по величине, как и токи I_A, I_B , I_C. Поэтому векторная диаграмма напряжений и токов в трехпроводной системе совпадает с векторной диаграммой в четырехпроводной системе.

При несимметричной нагрузке фазные напряжения на потребите­ле могут отличаться от одноименных фазных напряжений на генера­торе и в общем случае образует несимметричную систему векторов. Из-за отсутствия нулевого провода потенциал нулевой точки потре­бителей 0' не будет равным нулю. Однако остаются справедливыми соотношения:

__ __ __ __ __ __ __ __ __

U_AВ = U_A'- U_B', U_BС = U_B '- U_C' , U_CА =U_C' - U_A'

Положение нулевой точки 0' на векторной диаграмме можно найти следующим образом.

Измеряются фазные и линейные напряжения на потребителе и U₀ между нулевыми точками потребителя и генера­тора. Начинается построение векторной диаграммы с построения симметричной системы векторов фазных и линейных напряжений гене­ратора (см.рис.1). Далее из вершин треугольника А,В,С раствором циркуля, равным соответственно U_A', U_B', U_C' делаем засечки. Точка их пересечения соответствует потенциалу точки 0'. Соеди­нив точку 0' с вершинами треугольника, получим напряжения U_A', U_B', U_C'. Векторная диаграмма для несимметрич-ной нагрузки пред­ставлена на рис.4.

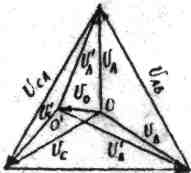
Рис.4.

Вектор, соединявший точки 00' есть U₀ . Он в масштабе должен со­ответствовать измеренному нап­ряжении между точками 00'.

Обрыв фазы и короткое за­мыкание в фазе потребителя мож­но считать несимметричной наг­рузкой и векторные диаграммы строить по принципу, описанно­му выше. Если но фазным напря-

жениям отложить фазные токи и найти их векторную сумму, можно убедиться, что при любой нагрузке

__ __ __

IA + IB + IC = 0.

Порядок выполнения работы

1.Ознакомиться с приборами и оборудованием и записать их техни­ческие данные в бланк отчета.

2.Собрать электрическую цепь согласно приложенной схеме. Прове­рить правильность её сборки с преподавателем.

3.Провести измерения токов и напряжений при различных режимах нагрузки согласно таблице 1, куда внести результаты измерений.

Таблица 1

Режим работы

Измерить

U12

U23

U31

U1

U2

U3

U0

I1

I2

I3

I0

В

В

В

В

В

В

В

А

А

А

А

Четырехпроводная система

1.Симметричная нагрузка 2.Несимметрич-ная нагрузка 3. Обрыв фазы при симметрич- ной нагруз­ке

Трехпроводная система

1.Симметричная нагрузка 2.Несимметрич-ная нагрузка 3. Обрыв фазы при симметрич- ной нагруз­ке 4.Короткое замыкание фазы при симметричной нагрузке

.

Режимы нагрузки:

1.Симметричная нагрузка: количество потребителей во всех фазах одинаково.

2.Несимметричная нагрузка: в одной фазе три потребителя, во вто­рой - два, в третьей - один.

3.Обрыв фазы имитируется отключением всех потребителей в одной фазе при симметричной нагрузке в двух других.

4.Короткое замыкание в одной фазе выполняется соединением нача­ла и конца этой фазы проводником при симметричной нагрузке в двух других фазах.

Содержание отчета

1.Технические характеристики всех измерительных приборов.

2.Схема электрической цепи.

3.Результаты измерений.

4.Векторные диаграммы напряжений и токов для всех режимов нагрузки.

5.Краткие выводы по работе.

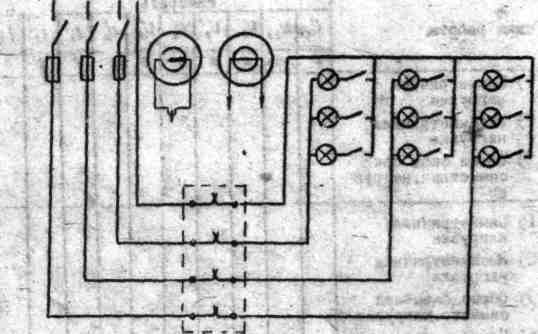
Схема исследования трехфазной системы при соединении потребителей "звездой"