Задание 4.

Вариант Построить комбинационную схему из элементов указанного базиса для логических функций:

Вариант	Базис	Функция
1	Булевский (И-ИЛИ-НЕ)
2	Пирса (ИЛИ-НЕ)
3	Шеффера (И-НЕ)
4	Булевский
5	Пирса
6	Шеффера
7	Булевский
8	Пирса
9	Шеффера

Варианты 10-15. Описать заштрихованные площади с помощью операций над множествами

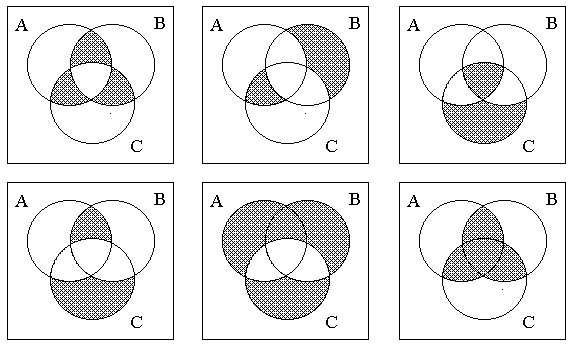Вар.10 Вар. 11 Вар. 12

Вар. 13 Вар. 14 Вар. 15

Вариант 16: A={0,1,2}, B={1,2}; Найти AB

Вариант 17: A={a1,a2,a3}, B={b1,b2,b3,b4}; Найти AB

Вариант 18: A={0,Δ,}, B={a,b,Δ}. Найти AB

Вариант 19: A={a, b, c}, B={b, c, d, e}. Найти C= (АВ).

Вариант 20: даны множества A и B, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (АВ).

Вариант 21: A={(a, b), (b, c)}, B={(b, c), (b, c, d), (c, d)}. Найти C= (АВ).

Вариант 22. Дано множество A={a, b, c}и универсальное множество U={a, b, c, d, e, f}. Найти C = .

Вариант 23: Дано множество A={{a, b}, c} и универсальное множество U={a, b, {a, b}, c, {d, e}, f}. Найти C= .

Вариант 24.: Даны множества A={a, b, c}, B={b, c, d, e}. Найти C= (А\В).

Вариант 25. Даны множества A и B, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (А\В).

Вариант 26: Приняв множество первых 20 чисел в качестве универсального множества U, записать следующие подмножества: А - множество четных чисел, В - множество нечетных чисел, С - множество квадратов чисел, D - множество простых чисел. Выполните операции (АВ), (АВ), (АС), (АD), (C\A), (C\D).

Вариант 27. Граф задан списком отношений (r_i – ребро, x_i – вершина):

rk

r1

r2

r3

r4

r5

r6

r7

ri

r11

r12

r13

r14

r15

r16

(xi;xj)

(x1;x2)

(x1;x3)

(x2;x5)

(x3;x4)

(x2;x4)

(x4;x6)

(x5;x6)

(xi;xj)

(x1;x3)

(x2;x4)

(x2;x5)

(x3;x4)

(x3;x5)

(x4;x5)

а) начертите граф;

б) составьте матрицу инциденции и матрицу смежности.

В ариант 28. Построить граф, заданный матрицей смежности:

0 1 1 0 1 0 0 0 0 0

1 0 0 1 1 0 0 0 0 0

1 0 0 0 1 0 0 0 0 0

0 1 0 0 1 0 0 0 0 0

1 1 1 1 0 1 1 0 0 0

0 0 0 0 1 0 1 0 0 0

a = 0 0 0 0 1 1 0 0 0 0

0 0 0 0 0 0 0 0 1 1

0 0 0 0 0 0 0 1 0 1

0 0 0 0 0 0 0 1 1 0

Варианты29-44. Минимизировать логическую функцию четырех переменных по карте Карно и представить ее аналитическое выражение.

Вариант 29. Вариант 30.

Х3Х4 Х1Х2	00	01	11	10		Х3Х4 Х1Х2	00	01	11	10
00	1			1		00		1		1
01			1			01	1			1
11	1					11	1			1
10	1			1		10		1	1