4.2.3 Построение фронтальной и горизонтальной проекции траектории движения солнца, относительно Земли
Построение ортогональных проекций траектории движения солнца относительно Земли необходимо для того, чтобы построить «инсоляционные линейки» для заданной даты и северной широты.
Строим фронтальную и горизонтальные проекции траектории движения солнца, относительно Земли (рис. 4.7).
На фронтальной проекции проведем окружность горизонтальным радиусом. Обозначим центр Т. Т – точка нахождения наблюдателя в данный час и на заданной широте. От линии горизонта откладываем углы дня и ночи. Получаем точки 12.00 и 00.00 на пересечении с окружностью. Соединив эти точки получаем фронтальную проекцию движения солнца вокруг Земли.
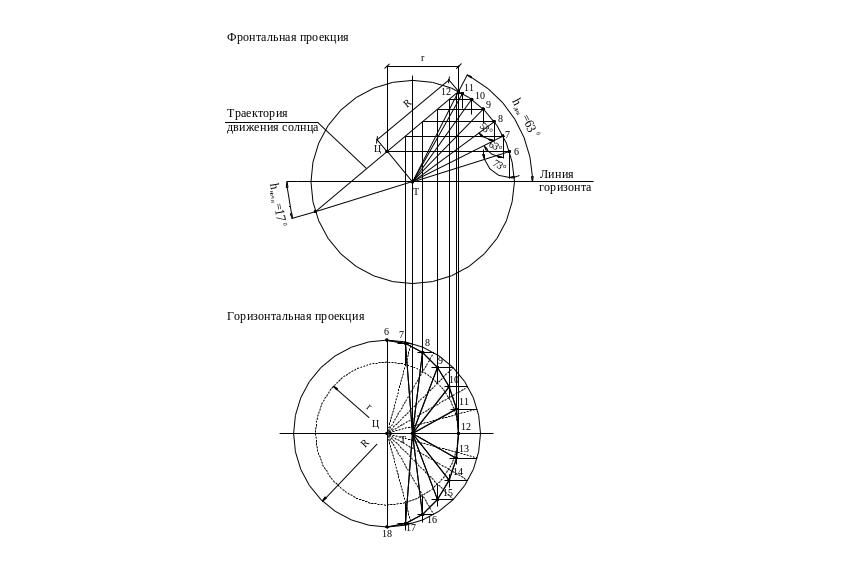
Рисунок 4.7 – Построение траектории движения Солнца
Из точки Т на траектории движения солнца вокруг Земли отбрасываем перпендикуляр и получаем точку Ц – центр вспомогательной окружности на горизонтальной проекции.
На горизонтальной проекции из проецируемой точки Ц проведем окружность радиусом R. Радиус R берем на фронтальной проекции.
Из точки Ц проведем еще одну вспомогательную окружность радиусом r. Длина r – проекция R на горизонтальную проекцию.
Полученные окружности условно делим на 12 частей (12 часов светового дня) по 150. Из полученных точек пересечения проводим перпендикуляры и получаем почасовые точки горизонтальной проекции движения солнца вокруг Земли.
Для того. чтобы получить «инсоляционную линейку» необходимо провести следующие геометрические построения:
1 Точки часов, расположенные на горизонтальной проекции траектории движения солнца спроецируем на фронтальную проекцию траектории движения солнца.
2 Полученные точки параллельно линии горизонта переносим на окружность и опускаем перпендикуляры.
3 Каждую точку окружности сводим в точку Т.
Полученный угол между перпендикуляром и вектором сведенным в точку Т – есть угол падения света на фронтальной проекции в определенный час, день и на заданной широте.
На кальке необходимо выделить «инсоляционные линейки» на фронтальной и горизонтальной проекциях для дальнейшего решения задач.
4.3 Определение направления длины тени от вертикального шеста
При наличии проекции орбиты солнца на заданной широте в характерную дату года легко находить направление и длину тени, отбрасываемой в заданное время вертикальным шестом.
ПРИМЕР 2 Определить направление и длину тени, отбрасываемой шестом высотой 0Н в день весеннего равноденствия в 11 часов солнечного времени на широте г. Харькова (φ = 500 с.ш.).
Совместить центр 0 проекции орбиты с местом установки шеста (рис. 2.3.1). Ось СЮ удобно при этом направить по вертикали. Продолжение отрезка 11 – 0 за точкой 0 будет искомым направлением тени. Длина тени равна произведению высоты шеста 0Н на котангенс высоты солнца в 11 часов. Графически это можно получить, изобразив шест вертикально прямой в принятом масштабе и проведя прямую под углом 900 - h0 от вершины шеста до линии земли.
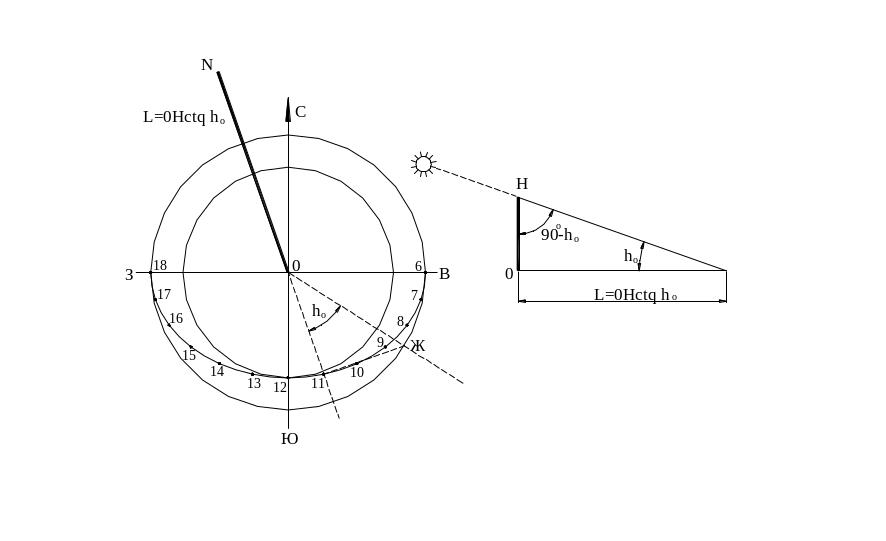
Рисунок 4.8 - Построение направления и длины тени от шеста 0Н
4.4 Определение продолжительности инсоляции и инсолируемой площади в комнате
ПРИМЕР 3 Определить продолжительность инсоляции и инсолируемую площадь пола комнаты, окно которой ориентировано на ЮВ в день весеннего равноденствия на широте г. Харькова (рис. 4.6).
С помощью графика координат солнца на широте 500 Гусева или с помощью построенной ранее проекции солнечной орбиты определим высоты и азимуты солнца в различные часы дня 22 марта. Отсчет часов начнем на 1 час после восхода и окончим за один час до захода
Часы |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
h0 |
10 |
20 |
27 |
34 |
39 |
40 |
39 |
34 |
27 |
20 |
10 |
А0 |
80 |
66 |
54 |
37 |
20 |
0 |
20 |
37 |
54 |
66 |
80 |
Вычертим вспомогательные проекции с изображением высоты стояния солнца h0 и азимута А0.
Рисунок 4.9 - Определение продолжительности инсоляции комнаты
На плане комнаты и на разрезе через грани откосов оконного проема прямые, параллельные соответственно азимуту и высоте солнца в 7 часов. Это будет началом инсоляции, а построение покажет контур солнечного пятна на полу. Далее проведем на плане диагональ оконного проема, которая соответствует предельно возможному случаю проникновения солнечного луча в комнату, и на вспомогательном графике – прямую, параллельную ей, которая укажет время конца инсоляции – 13 ч. 40 минут. Продолжительность инсоляции получается 13 ч. 40 мин. – 7 = 6 ч. 40 минут. Построение солнечного пятна в конечный и промежуточные моменты времени (с интервалом 1 или 2 часа) проводится аналогично построению в начальный момент. Соединив крайние точки солнечных пятен, выявим общую площадь инсолируемых участков на полу комнаты.