4.2 Построение проекции орбиты солнца

4.2.1 Построение проекции орбиты солнца в дни равноденствия

Для выполнения инсоляционных расчетов в ряде случаев удобно знать путь движения солнца не в отдельные моменты времени, а непрерывно на протяжении дня. Такое представление дают проекции орбиты солнца на горизонтальную плоскость. Построение такой проекции наиболее просто осуществимо для дней весеннего и осеннего равноденствия. В эти дни солнце восходит в 6 часов утра на Востоке и заходит в 18 часов на Западе.

Проекция орбиты на фронтальную плоскость – прямая, наклонная к горизонту под углом 90⁰ – φ (φ – географическая широта пункта).

На горизонтальную плоскость круговая орбита проектируется в виде эллипса, малая полуось которого равна проекции луча солнца на плоскость земли в 12 часов.

Построение эллипса может быть выполнено на совмещенных вертикальной и горизонтальной проекциях в следующем порядке (рис. 4.4).

Из точки 0 произвольным радиусом проводим окружность, представляющую условно линию горизонта. От линии 0З откладываем вниз угол А0З, равный углу φ. Прямая 0А является проекцией на вертикальную плоскость траектории солнца в дни равноденствия.

Далее разделим дугу ВЮЗ на 12 равных частей, каждая из которых соответствует 15⁰, т.е. одному часу времени. Из точки 0 проведем вспомогательную окружность радиусом r, равным проекции половины малой оси эллипса, после чего соединим точки деления дуги В0З с точкой 0. Из точек деления большой окружности проведем прямые, параллельные оси ЮС, а из точек пересечения радиусов с малой окружностью – прямые, параллельные оси ВЗ. Одноименные точки пересечения определят очертания эллипса и его деления на часовые участки.

Для нахождения азимута солнца по полученному графику, в какой либо момент времени, например в 11 часов, необходимо соединить точку 11 на эллипсе с центром 0. Соединив точки Ю0 и 11 – 0 получим угол азимута солнца в 11 часов. Восстановить в точке 11 перпендикуляр к прямой 11 - 0 до пересечения его с окружностью в точке Ж и соединить точку Ж с точкой 0. Угол между направлениями 0 – 11 и 0Ж является искомой величиной высоты солнца h₀ в 11 часов в день равноденствия для пункта, находящегося на географической широте φ. Следовательно А_в = 20⁰, а h₀ = 40⁰.

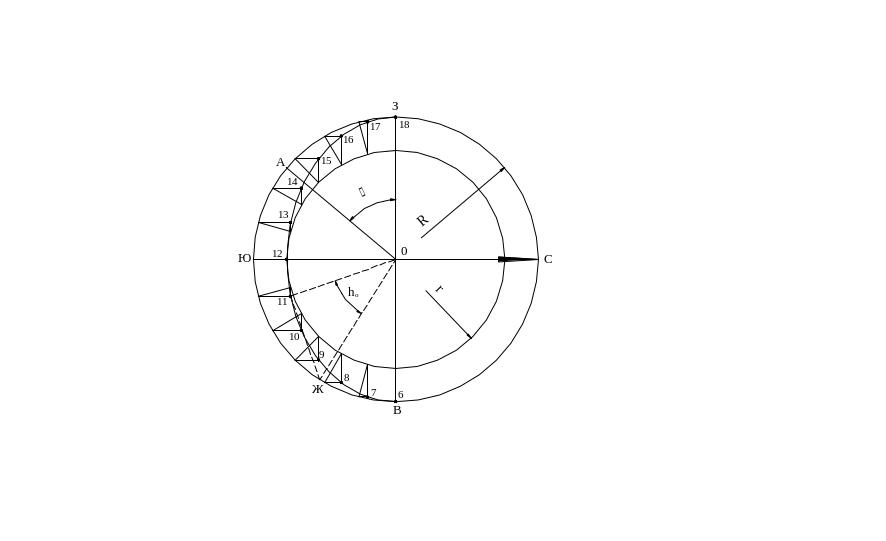
Рисунок 4.4 - Построение проекции орбиты солнца в дни равнодействия

Проекцию орбиты солнца можно выявить графическим построением не только для дней равноденствия, но также для дней летнего и зимнего солнцестояния и любого дня года.

Высота стояния солнца в 12 часов самого длинного в году дня 21.VI – максимальна и равна h₀ = (90 - φ) +23,5⁰.

Проекция летней траектории солнца сохраняет форму эллипса, но точки восхода и захода солнца смещаются от оси ВЗ к северу, так как плоскость орбиты проходит выше, чем в дни равноденствия (но остается параллельной плоскости орбиты в те дни).

4.2.2 Построение проекции орбиты солнца для

определенного календарного дня и заданной широты

Для решения задач, данных в приложении Б, определяемых в заданной широте и для заданной даты необходимо построить «инсоляционные линейки». Для этого необходимо построить фронтальную и горизонтальную проекции траектории движения солнца относительно земли:

1 Определяем месторасположения земли на орбите – угол β (рис. 4.4)

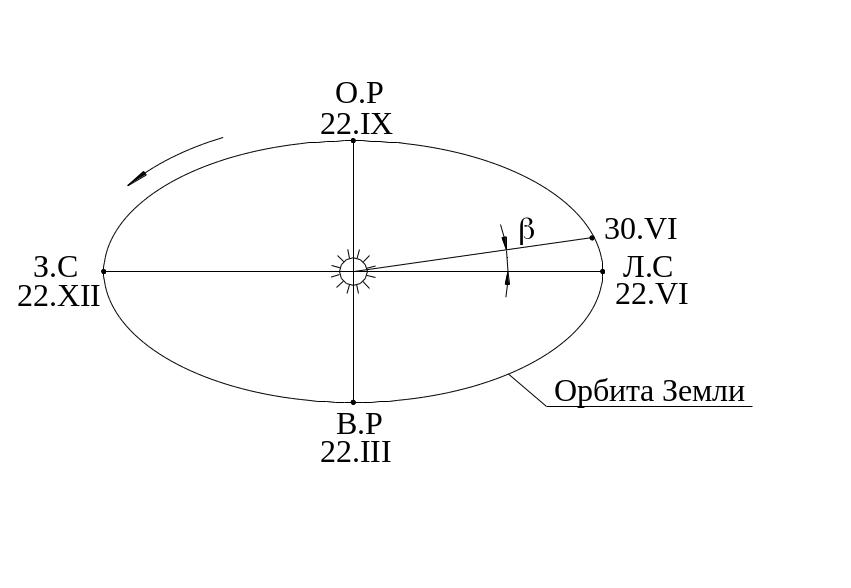
Л.С – летнее солнцестояние (принимается за точку отсчета – условный «0»).

О.Р – осеннее равноденствие.

В.Р – весеннее равноденствие.

З.С – зимнее солнцестояние

Рисунок 4.4 - Месторасположения земли на орбите

Один календарный день равен одному градусу.

Дней в году 365 (366) ≈ градусов в окружности 360.

Например: угол β для 30.VI равен 8⁰. Между 22.VI и 30.VI 8 календарных дней.

2 Определяем угол между световым вектором и северным направлением оси Земли – угол Θ (рис. 4.5).

Угол Θ определяется из зависимости:

сos Θ = -0,4 сos β, откуда Θ = arcos (-0,4 сos β).

Например: сos Θ = -0,4 сos 8⁰, Θ = arcos (-0,4 · 0,99) = 113⁰.

Угол Θ должен находиться в пределах:

90 + 23,5 = 113,5

90 – 23,5 = 66,5, так как угол наклона оси Земли от условного перпендикуляра равен 23,5⁰.

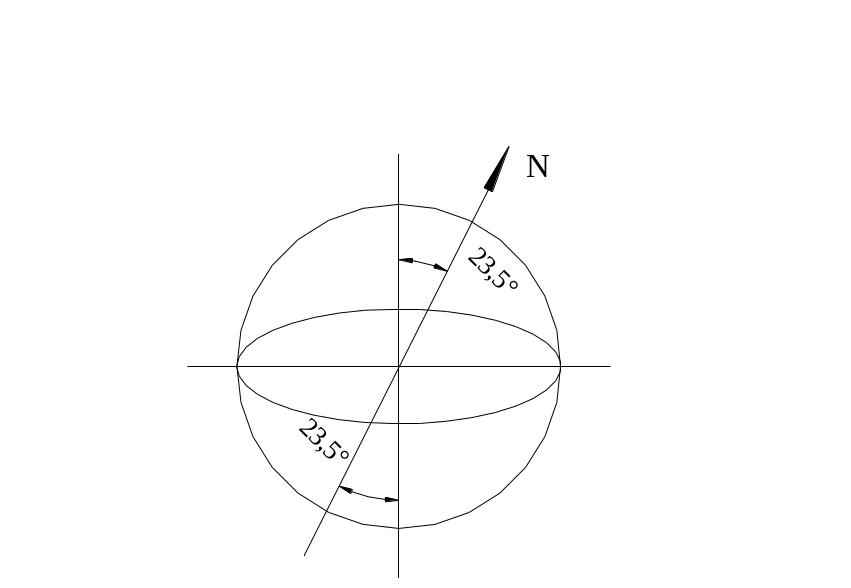
Рисунок 4.5 – Угол наклона оси Земли

3 Определяем углы дня и ночи (угловые высоты дня и ночи).

Углы дня и ночи можно определить двумя способами: аналитическим и графическим.

Аналитический способ:

h_дня = Θ – с.ш.,

h_ночи = Θ + с.ш. - 180⁰.

Например:

h_дня = 113⁰ – 50⁰ = 63⁰,

h_ночи = 113⁰ + 50⁰ - 180⁰ = -17⁰.

Графический способ:

Произвольным радиусом проведем окружность Земли (рис. 4.6). От вспомогательной горизонтальной линии отложим угол Θ, соответственно получаем ось Земли и перпендикулярно ей линию экватора. От линии экватора откладываем угол северной широты (с.ш.). Через точку полученную на окружности Земли параллельно экватору проведем вспомогательную линию и получим точки дня и ночи. Через полученные точки проведем касательные. Полученные углы между солнечным вектором и касательными и есть угловые высоты дня и ночи - h_дня, h_ночи.

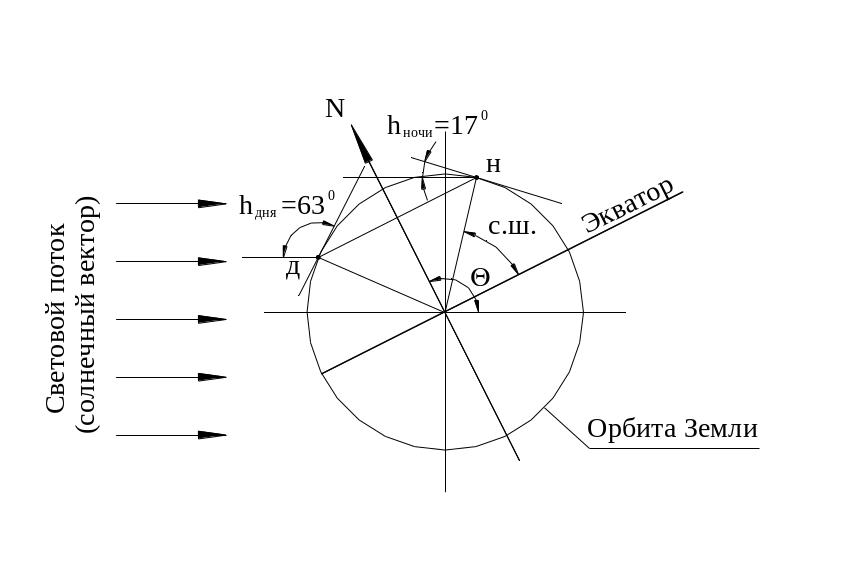
Рисунок 4.6 – Построение углов дня и ночи

Сравним результаты, полученные аналитическим и графическим способами.