1. Линейная модель множественной регрессии.

Линейная модель множественной регрессии. У=а₀+а₁х₁+ а₂х₂+…+ а_mх_m+e

Параметры определяются с помощью методов наименьших квадратов.

Для этого проведем все рассуждения в матричной форме. Введем следующие матричные обозначения:

;

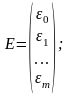
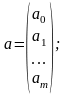
где У вектор n значений результативного показателя.

Х – матрица n значений m независимых переменных; а матрица параметров

У=Х∙а+ε.

Заметим, что а – выборочные оценки совокупности.

Итак, метод наименьших квадратов требует мин-ии суммы квадратов отклонений исходных модели значений

,

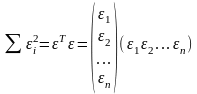
Далее:

Из матричной алгебры известно, что , тогда:

1 – это есть матрица размерностью 1Х1, т.е. число-скаляр, а скаляр при трансформировании не меняется, поэтому 

Согласно условию экстремума S по а =0

;

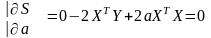
2Х^ТY+2aX^TX=0

X^TY=aX^TX

Для погашения а умножим обе части этого уравнения на (ХТХ)-1, тогда

а= (X^TХ)^-1∙X^TY

Решение задачи нахождения матицы, а возможно лишь в том случае, если строки и столбцы матрицы Х линейно независимы.

2. Метод наименьших квадратов (МНК).

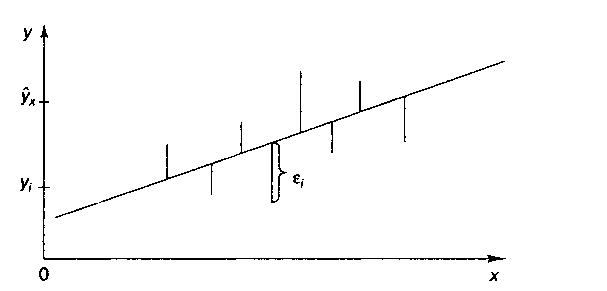
Классический подход к оцениванию параметров линейной регрессии основан на метода наименьших квадратов. МНК позволяет получить такие оценки параметров а и Ь, при которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических) у_х ми­нимальна:

Иными словами, из свего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной: , следовательно,

Чтобы найти минимум ф-ции , надо вычислить частные производные по кажд. из параметров а и b и приравнять их к нулю. Обозначим 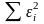через S, тогда: ;

Преобразуя эту формулу, получим следующую систему нормальных уравнений для оценки параметров а и b:

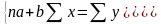
Решая эту систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. .

3. Свойства оценок МНК.

В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условиярегрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если, во-первых, математическое ожидание случайных ошибок равно нулю, во-вторых, факторы и случайные ошибки — независимые случайные величины. Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).

Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы   к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были еще и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:

• Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности): 

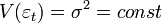
• Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой 

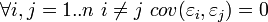
Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок 

Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:

Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.

Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболееэффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.

4. Показатели качества регрессии.

5. Линейные регрессионные модели с гетероскедастичными остатками.

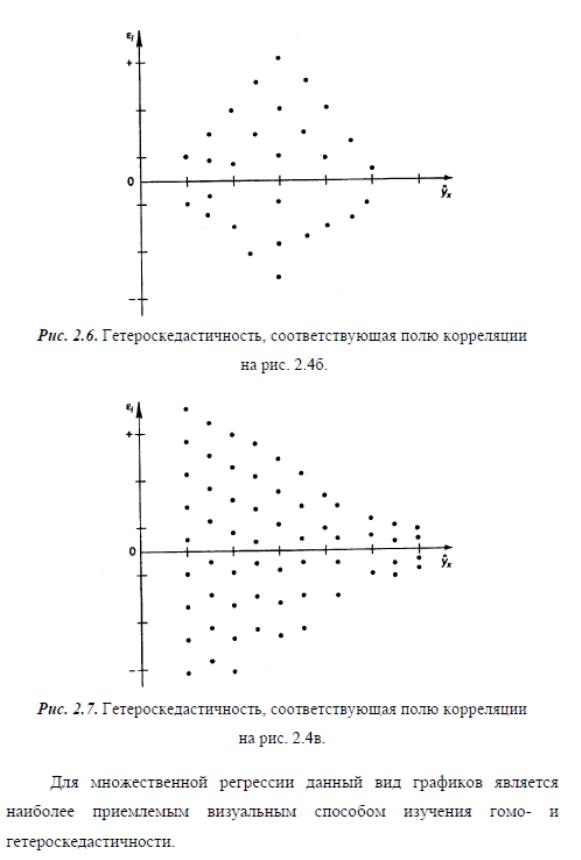
6. Линейные регрессионные модели с автокоррелированными остатками.

7. Обобщенный метод наименьших квадратов (ОМНК).

Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков  , где   - некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение  . Следовательно, указанный функционал можно представить следующим образом  , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных "остатков". Таким образом, можно выделить класс методов наименьших квадратов - LS-методы (Least Squares).

Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т.н.обобщенного МНК (ОМНК, GLS - Generalized Least Squares) - LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок:  .

Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид

Ковариационная матрица этих оценок соответственно будет равна

Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования - для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.

8. Регрессионные модели с переменной структурой (фиктивные переменные).

9. Нелинейные модели регрессии и их линеаризация.

При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются по МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию , мы преобразовываем ее в линейный вид: , где переменные выражены в логарифмах. Далее обработка МНК та же: строится система нормальных уравнений и определяются неизвестные параметры. Потенцируя значение  , находим параметр a и соответственно общий вид уравнения степенной функции. Вообще говоря, нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Эта оценка определяется, как и в линейной регрессии, МНК. Так, в двухфакторном уравнении нелинейной регрессии может быть проведена линеаризация, введением в него новых переменных  . В результате получается четырехфактороное уравнение линейной регрессии .

10. Характеристики временных рядов.

Обычно эконометрические модели строятся на основе двух типов исходных данных:

 данные, характеризующие совокупность различных объектов в определенный момент (период) времени;

 данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

 факторы, формирующие тенденцию ряда (например, инфляция влияет на увеличение размера средней заработной платы);

 факторы, формирующие циклические колебания ряда (например, уровень безработицы в курортных городах в зимний период выше по сравнению с летним);

 случайные факторы.

Очевидно, что реальные данные чаще всего содержат все три компоненты. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Если же временной ряд представлен как их произведение, то такая модель называется мультипликативной.

При наличии в временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют уровнями автокорреляцией уровней ряда. Количественно эту зависимость с помощью коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутого на несколько шагов во времени.

Пример. Пусть имеются условные данные о средних расходах на конечное потребление ( , денежных единиц) за 8 лет.

1	7	-	-	-	-	-	-
2	8	7	-3,39	-3	9,87	10,8241	9
3	8	8	-3,29	-2	6,58	10,8241	4
4	10	8	-1,29	-2	2,58	1,6641	4
5	11	10	-0,29	0	0,00	0,0841	0
6	12	11	0,71	1	0,71	0,5041	1
7	14	12	2,71	2	5,42	7,3441	4
8	16	14	4,71	4	18,84	22,1841	16
	86	70	-0,03	0	44,0	53,4287	38

По формулам

вычисляем

,

.

Далее, заполняем таблицу и используя формулу для вычисления линейного коэффициента корреляции, получаем

.

Полученное значение свидетельствует об очень тесной зависимостью между расходами на конечное потребление текущего непосредственно предшествующего годов и, следовательно, о наличии во временном ряде расходов на конечное потребление сильной линейной тенденции.

Нами был посчитан коэффициент автокорреляции для смещения на один год. Такой коэффициент называется коэффициентом первого порядка. При смещении на два года получим коэффициент второго порядка и так далее. Число периодов (в данном случае лет), по которым рассчитывается коэффициент автокорреляции, называется лагом.

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени. Поскольку зависимость может принимать различные формы, то ее формализации можно использовать различные виды функций: линейную, гиперболическую, параболическую, степенную и т.п. Параметры каждой из перечисленных моделей могут быть найдены по МНК.

11. Модели стационарных и нестационарных временных рядов, их идентификация.

В теоретических и прикладных исследованиях рассматривают широкий спектр моделей временных рядов. Выделим сначала стационарные модели. В них совместные функции распределения   для любого числа моментов времени k, а потому и все перечисленные выше характеристики временного ряда не меняются со временем. В частности, математическое ожидание и дисперсия являются постоянными величинами, автокорреляционная функция зависит только от разности t-s. Временные ряды, не являющиеся стационарными, называются нестационарными.

Под идентификацией моделей обычно понимают выявление их структуры и оценивание параметров. Поскольку структура - это тоже параметр, хотя и нечисловой (см. главу 8), то речь идет об одной из типовых задач эконометрики - оценивании параметров.

Проще всего задача оценивания решается для линейных (по параметрам) моделей с гомоскедастичными независимыми остатками. Восстановление зависимостей во временных рядах может быть проведено на основе методов наименьших квадратов и наименьших модулей, рассмотренных в главе 5 моделей линейной (по параметрам) регрессии. На случай временных рядов переносятся результаты, связанные с оцениванием необходимого набора регрессоров, в частности, легко получить предельное геометрическое распределение оценки степени тригонометрического полинома.

Однако на более общую ситуацию такого простого переноса сделать нельзя. Так, например, в случае временного ряда с гетероскедастичными и автокоррелированными остатками снова можно воспользоваться общим подходом метода наименьших квадратов, однако система уравнений метода наименьших квадратов и, естественно, ее решение будут иными. Формулы в терминах матричной алгебры, о которых упоминалось в главе 5, будут отличаться. Поэтому рассматриваемый метод называется "обобщенный метод наименьших квадратов (ОМНК)" (см., например, [3, с.212]).

Замечание. Как уже отмечалось в главе 5, простейшая модель метода наименьших квадратов допускает весьма далекие обобщения, особенно в области системам одновременных эконометрических уравнений для временных рядов. Для понимания соответствующей теории и алгоритмов необходимо профессиональное владение матричной алгеброй. Поэтому мы отсылаем тех, кому это интересно, к литературе по системам эконометрических уравнений [4-9] и непосредственно по временным рядам [10-25], в которой особенно много интересуются спектральной теорией, т.е. выделением сигнала из шума и разложением его на гармоники. Подчеркнем в очередной раз, что за каждой главой настоящей книги стоит большая область научных и прикладных исследований, вполне достойная того, чтобы посвятить ей много усилий. Однако из-за ограниченности объема книги мы вынуждены изложение сделать конспективным.

12. Система линейных одновременных уравнений.

Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизмов их функционирования. При использовании отдельных уравнений регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной повлечет за собой изменения во всей системе взаимосвязанных признаков. Этим объясняется необходимость использования не отдельных уравнений, а их систем.

Система уравнений в эконометрических исследованиях может быть построена по-разному.

Возможна система независимых уравнений, когда каждая зависимая переменная рассматривается как функция одного и того же набора факторов:

Примером такой модели может служить модель экономической эффективности сельскохозяйственного производства, где в качестве зависимых переменных выступают показатели эффективности производства (производительность, себестоимость продукции и т.д.), а в качестве факторов – характеристики самого хозяйства (количество голов скота, площадь пашни и т.д.).

Для системы независимых уравнений каждое уравнение может рассматриваться самостоятельно, и его параметры определяются обычным образом по методу наименьших квадратов.

Наибольшее распространение в эконометрических исследованиях получила система взаимосвязанных уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть системы, а в других – в правую часть:

Система взаимосвязанных уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. Каждое уравнение такой системы не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются его модификации: косвенный, двухшаговый и трехшаговый метод наименьших квадратов.

Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида

где - темп изменения месячной заработной платы;

- темп изменения цен;

- процент безработных;

- темп изменения постоянного капитала;

- темп изменения цен на импорт сырья.

Второй вариант

Эконометрика – это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов. Эта наука возникла в результате взаимодействия и объединения трех компонент: экономической теории, статистических и экономических методов. Становление и развитие эконометрики происходили на основе так называемой высшей статистики, когда в уравнение регрессии начали включаться переменные не только в первой, но и во второй степени. В ряде случаев это необходимо для отражения свойства оптимальности экономических переменных, т.е. наличия значений, при которых достигается минимальное или максимальное воздействие на зависимую переменную. Таково, например, влияние внесения в почву удобрений на урожайность: до определенного уровня насыщение почвы удобрениями способствует росту урожайности, а по достижении оптимального уровня насыщения удобрениями его дальнейшее наращивание не приводит к росту урожайности и даже может вызвать ее снижение.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными – y и x, т.е. модель вида

,

где y – зависимая переменная (результативный признак);

x – независимая переменная (признак-фактор).

Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида

.

Простая регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Однако когда уверенности в правомерности такого допущения нет, необходимо использовать модель с большим числом факторов. Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства и целого ряда других вопросов эконометрики. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Суть этой проблемы включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции.

Линейная модель множественной регрессии

В линейной множественной регрессии

(1)

параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего параметра на единицу при неизменном значении других факторов, закрепленных на среднем уровне.

Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:

,

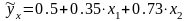где y – расходы семьи за месяц на продукты питания, тыс. руб.;

x₁ – месячный доход на одного члена семьи, тыс. руб.;

x₂ – размер семьи, человек.

Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Первый параметр не подлежит экономической интерпретации.

Классический подход к оцениванию параметров линейной модели основан на методе наименьших квадратов (МНК).

Этот метод позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (y) от расчетных (теоретических) минимальна:

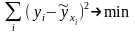. (2)

Чтобы найти минимум функции (2), надо вычислить производные по каждому из параметров и приравнять их к нулю, т.к. равенство нулю производной – необходимое условие экстремума. В результате получается система уравнений, решение которой и позволяет получить оценки параметров регрессии.

Так, для уравнения (1) система нормальных уравнений имеет вид:

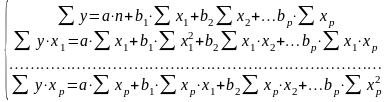(3)

Решение системы (3) может быть осуществлено по одному из известных способов: Метод Гаусса, метод Крамера и т.д.

Пример. По четырем предприятиям региона (см. табл.) изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%). Требуется написать уравнение множественной регрессии.

Номер предприятия	1	2	3	4
, (%)	1	2	3	5
, (%)	0	1	3	4
, (тыс. руб.)	6	11	19	28

Решение

Предположим, что зависимость выработки продукции на одного работника характеризуется следующим уравнением:

.

На основании исходных данных составляем систему уравнений для определения коэффициентов 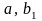и .

;

; ;

;

;

; ;

.

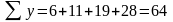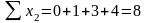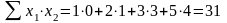Решим эту систему по методу Крамера. Вычисляем определитель системы:

Аналогично вычисляем частные определители, заменяя соответствующий столбец столбцом свободных членов:

; ; .

Коэффициенты уравнения определяются по формулам:

Таким образом, уравнение имеет вид:

.

Возможен и иной подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

, (4)

где - стандартизованные переменные: , для которых среднее значение равно нулю, а среднее квадратическое значение равно единице;

- стандартизованные коэффициенты регрессии.

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида для определения стандартизованных коэффициентов регрессии.

. (5)

Следует отметить, что величины и называются парными коэффициентами корреляции и определяются по формулам

, . (6)

Решая систему (5) определяем стандартизованные коэффициенты регрессии. Сравнивая их друг с другом, можно ранжировать факторы по силе воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Пример. Получим для предыдущего примера уравнение регрессии в стандартизованном масштабе.

, , ,

;

;

.

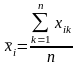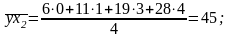
Согласно (5) получаем систему нормальных уравнений в виде:

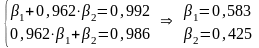
Окончательно получаем уравнение регрессии в стандартизованном масштабе в виде:

Используя формулы можно вернуться к уравнению «чистой» регрессии:

Сравнивая полученное уравнение с полученным ранее мы видим хорошее соответствие полученных разными способами результатов.