41 . Метод наименьших квадратов (мнк).

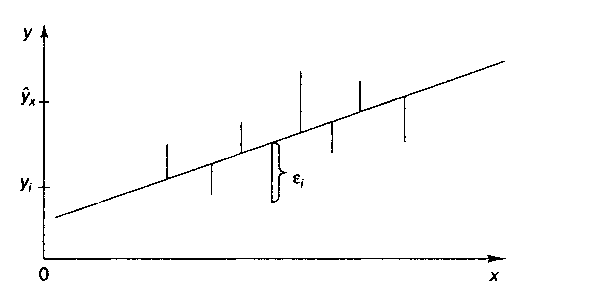
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов. МНК позволяет получить такие оценки параметров а и Ь, при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) у_х ми­нимальна:

Иными словами, из всего множества линий, линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной: , следовательно,

Чтобы найти минимум ф-ции , надо вычислить частные производные по кажд. из параметров а и b и приравнять их к нулю. Обозначим через S, тогда: ;

Преобразуя эту формулу, получим следующую систему нормальных уравнений для оценки параметров а и b:

Решая эту систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. .

Метод наименьших квадратов дает алгоритм расчетов в случае, если исходные данные – по-прежнему набор n пар чисел (t_k , x_k), k = 1,2,…,n, где t_k – независимая переменная (например, время), а x_k – зависимая (например, индекс инфляции - см. главу 7), а восстанавливать надо не линейную зависимость, а квадратическую:

Следует рассмотреть функцию трех переменных

Оценки метода наименьших квадратов - это такие значения параметров a*, b* и с*, при которых функция  f(a,b,с) достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b,с) по аргументам a, b и с, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:

Приравнивая частную производную к 0, получаем линейное уравнение относительно трех неизвестных параметров a,b,c:

Приравнивая частную производную по параметру b к 0, аналогичным образом получаем уравнение

Наконец, приравнивая частную производную по параметру с к 0, получаем уравнение

Решая систему трех уравнений с тремя неизвестными, находим оценки метода наименьших квадратов.

42. Свойства оценок мнк.

В тех случаях, когда предпосылки выполняются, оценки, полученные по МНК, будут обладать свойствами линейности, нормальности, несмещённости, состоятельности и эффективности.

1) ЛИНЕЙНОСТЬ – это оценка является линейной, если она является линейным функционалом

2) НОРМАЛЬНОСТЬ - оценка является нормальной, если ее распределение -нормально

3) НЕСМЕЩЕННОСТЬ оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойствами несмещённости, то их можно сравнивать по разным исследованиям. Оценка является несмещенной, если ее математическое ожидание равно истинному значению параметра.

4) ЭФФЕКТИВНОСТЬ. Для практических целей важна не только несмещённость, но и эффективность оценок. Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещённость оценки должна дополняться минимальной дисперсией.

5) СОСТОЯТЕЛЬНОСТЬ. Степень достоверности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещёнными и эффективными, но и состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объёма выработки.

Теорема: Если оценка параметра несмещенная, а ее дисперсия стремится к нулю, то она – состоятельна