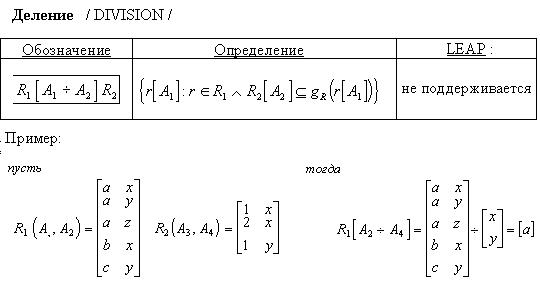4.3. Диаграммы взаимодействия

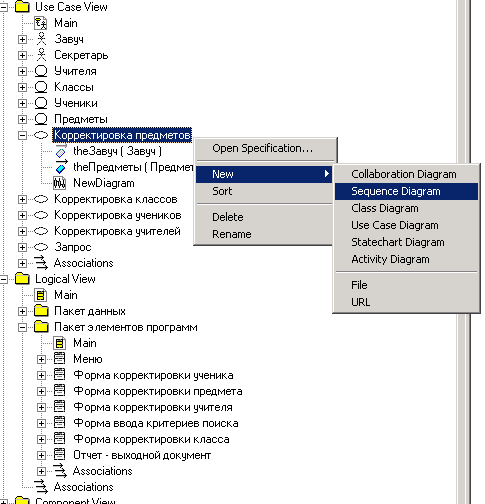
На диаграмме взаимодействия отображают один из процессов обработки информации в функции. Такие диаграммы изображаются для каждой функции. Мы рассмотрим один из видов диаграмм взаимодействия – диаграммы последовательностей (Sequence). Диаграммы взаимодействия визуализируют объекты и сообщения (с помощью сообщений один объект запрашивает у другого выполнения конкретной функции). Диаграмма последовательности – это графическое изображение сценария, который показывает взаимоотношения объектов во временной последовательности – что произошло вперед, что произошло потом. Диаграмма Sequence создается в представлении Use Case. Для ее создания следует нажать правую кнопку мыши при нахождении курсора на соответствующей функции в списке объектов:

Sequence диаграммы читаются сверху вниз. Вверху размещаются объекты, у каждого объекта имеется линия жизни. Сообщения рисуют между линиями жизни объектов. Сообщение показывает, что один объект вызывает функцию другого (того, к которому оно направлено). Сообщение может направляться другому объекту или самому себе.

Период контроля показывает период времени, в течение которого объект выполняет действия.

Пример диаграммы последовательности (Рис. 10).

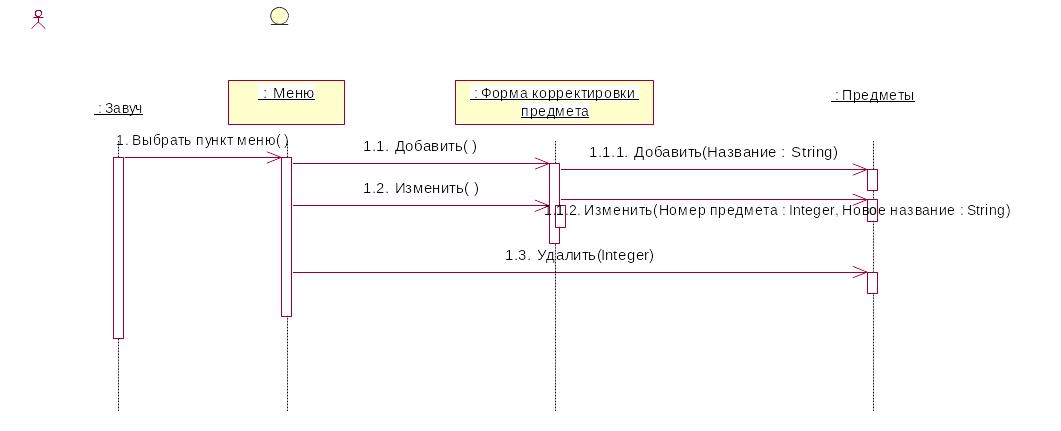
Рис. 10

Сообщения на диаграмме нумеруются либо последовательно, либо иерархически.

Последовательная нумерация присваивает последовательные номера сообщениям. Для включения такой нумерации нужно в пункте меню Tools, Options выбрать закладку Diagram и включить Sequence Numbering. Для иерархической нумерации нужно дополнительно включить Hierarchical Messages

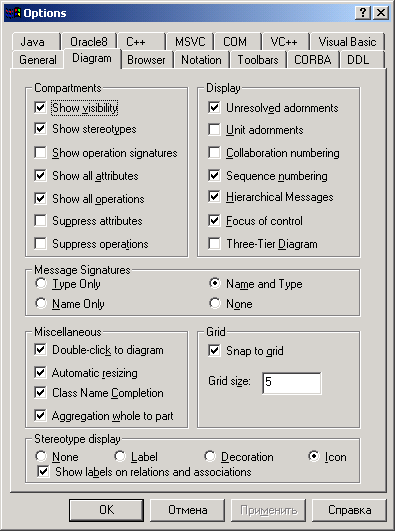
Иерархическая нумерация основана на зависимых сообщениях.

При перемещении сообщения по вертикали все зависимые сообщения также перемещаются.

Действующие лица и объекты (Формы, Отчеты и Сущности) выбираются из левого столбца диаграммы (это уже созданные классы), а связи между ними -из списка названий методов при установке новой связи.

5. Лабораторная работа 2

Задание: На основании заданной постановки задачи бригада студентов выполняет следующие действия:

1. Разработка диаграммы сценариев с помощью пакета Rational Rose.

2. Разработка диаграммы классов с помощью пакета Rational Rose.

3. Разработка диаграмм последовательности с помощью пакета Rational Rose.

Состав отчета:

1. Диаграмма сценариев.

2. Диаграмма классов (пакет данных и пакет элементов программ).

3. Диаграммы последовательности.

После разработки концептуальной и логической модели базы данных и построения объектной модели решаемой задачи можно приступать к разработке приложения баз данных.

Прежде чем рассматривать различные технологии их разработки, познакомимся с реляционной алгеброй и языком SQL, на которых основано большинство реляционных систем управления базами данных (СУБД).

6. Реляционная алгебра и язык sql

6.1. Основы реляционной алгебры

Доступ к реляционным данным осуществляется при помощи реляционной алгебры. Основная идея реляционной алгебры состоит в том, что коль скоро отношения являются множествами, то средства манипулирования отношениями могут базироваться на традиционных теоретико-множественных операциях, дополненных некоторыми специальными операциями, специфичными для баз данных.

Рассмотрим вариант алгебры, который был предложен Коддом. Набор основных алгебраических операций состоит из восьми операций, которые делятся на два класса - теоретико-множественные операции и специальные реляционные операции. В состав теоретико-множественных операций входят операции:

• объединения отношений;

• пересечения отношений;

• взятия разности отношений;

• прямого произведения отношений.

Специальные реляционные операции включают:

• ограничение отношения;

• проекцию отношения;

• соединение отношений;

• деление отношений.

Операндами каждой такой операции является одно или несколько отношений, результатом выполнения операции всегда является новое отношение.

В рассмотренных ниже примерах используются следующие отношения:

P(D1,D2,D3) Q(D4,D5) R(M,P,Q,T) S(A,B)

1 11 x x 1 x 101 5 a 5 a

2 11 y x 2 y 105 3 a 10 b

3 11 z y 1 z 500 9 a 15 c

4 12 x w 50 1 b 2 d

w 10 2 b 6 a

w 300 4 b 1 b.

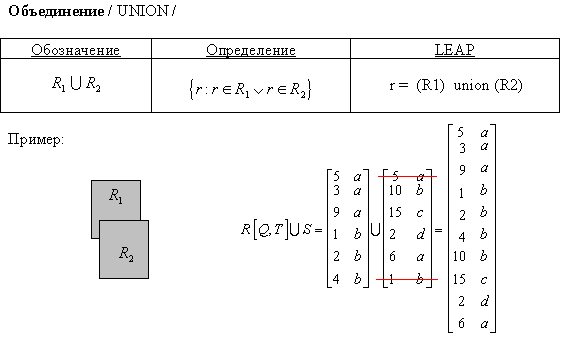
• ОБЪЕДИНЕНИЕ Отношения-операнды в этом случае должны быть определены по одной схеме. Результирующее отношение содержит все строки операндов, за исключением повторяющихся.

 

• ПЕРЕСЕЧЕНИЕ На входе операции два отношения,  определенные по одной схеме. На выходе - отношение, содержащие кортежи, которые присутствуют в обоих исходных отношениях.

 

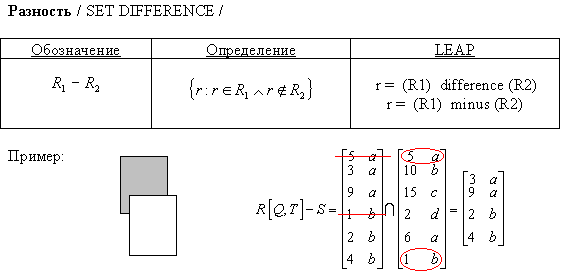
• РАЗНОСТЬ Операция, во многом похожая на ПЕРЕСЕЧЕНИЕ, за исключением того, что в результирующем отношении содержатся кортежи, присутствующие в первом и отсутствующие во втором исходных отношениях.

 

• ДЕКАРТОВО ПРОИЗВЕДЕНИЕ

Входные отношения могут быть определены по разным схемам. Схема результирующего отношения включает все атрибуты исходных. Кроме того:

• степень результирующего отношения равна сумме степеней исходных отношений;

• мощность результирующего отношения равна произведению мощностей исходных отношений.

 

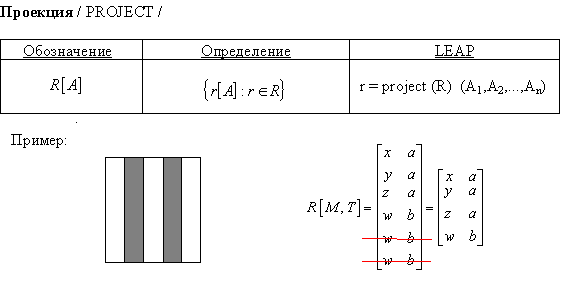
• ПРОЕКЦИЯ (ВЕРТИКАЛЬНОЕ ПОДМНОЖЕСТВО)

Операция проекции представляет собой выборку из каждого кортежа отношения значений атрибутов, входящих в список A, и удаление из полученного отношения повторяющихся строк.

 

• ВЫБОРКА (ОГРАНИЧЕНИЕ, ГОРИЗОНТАЛЬНОЕ ПОДМНОЖЕСТВО) На входе используется одно отношение, результат - новое отношение, построенное по той же схеме, содержащее подмножество кортежей исходного отношения, удовлетворяющих условию выборки.

 

• СОЕДИНЕНИЕ Данная операция имеет сходство с ДЕКАРТОВЫМ ПРОИЗВЕДЕНИЕМ. Однако здесь добавлено условие, согласно которому вместо полного произведения всех строк в результирующее отношение включаются только строки, удовлетворяющие определенному соотношению между атрибутами соединения (А₁,A₂) соответствующих отношений.

 

• ДЕЛЕНИЕ

Пусть отношение R , называемое делимым, содержит атрибуты (A₁,A₂,...,A_n). Отношение S - делитель содержит подмножество атрибутов A: (A₁,A₂,...,A_k) (k<n). Результирующее отношение C определено на атрибутах отношения R, которых нет в S, т.е. A_k+1,A_k+2,...,A_n. Кортежи включаются в результирующее отношение C только в том случае, если его декартово произведение с отношением S содержится в делимом R.