Задача про максимальний потік.

0fijcij

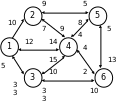
Постановка задачі:

потрібно визначити пропускну спроможність мережі або максимальний потік, а також найбільш напружені вузли (за водозбиранням), найбільш напружені дуги (дуги, у яких фактичний оборот максимально наближений до пропускної спроможності).

fij  [0, Cij] – змінна, яку ми повинні знайти

0fijcij

cij - пропускна спроможність.

Опис алгоритму.

Алгоритм базується на основі циклу, тобто до тих пір, доки будується ланцюжок S (T).

1. ітерація:

доки існує “ST”

• генерація такого ланцюжка “ST”;

• обчислення  =min{Cij}

• із прямих відняти :

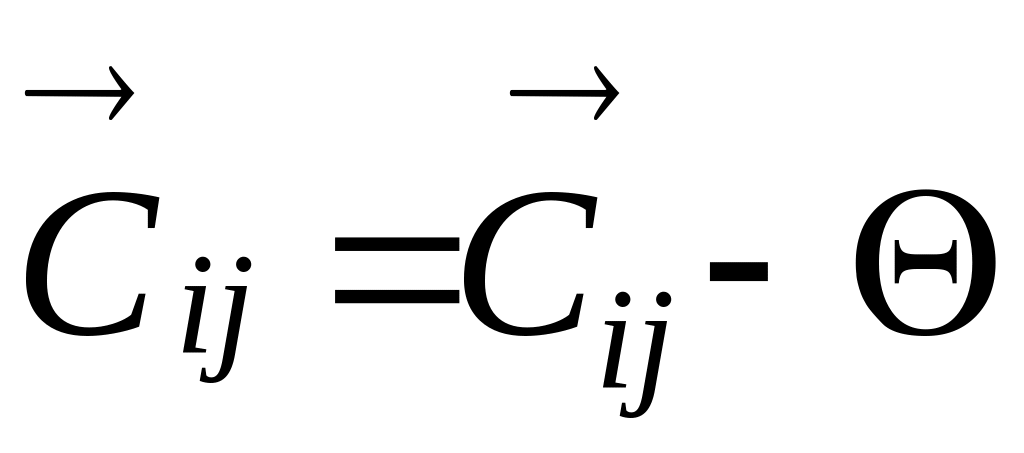
• до обернених чисел (в оберненому напрямку) додати :

2. ущільнення максимального потоку {F}:

Примітка: Алгоритм буде правильним, якщо сума за першим рядком дорівнює сумі останнього стовпчика, а також: сума за i-тим рядком дорівнює сумі i-того стовпчика (закон Кірхгофа).

П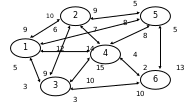 риклад.

9

0

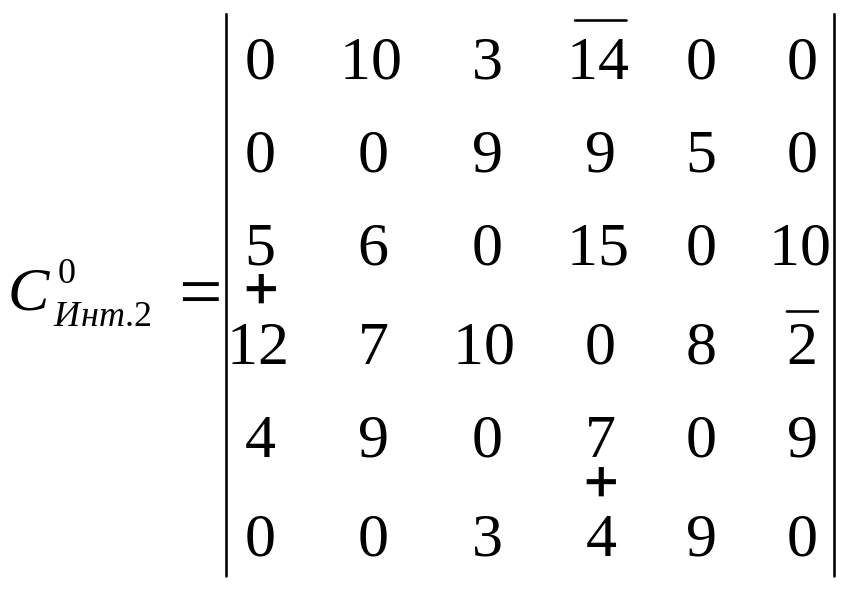
Ітерація 1 Ітерація 2

16 немає 146  = 2

156  = 4

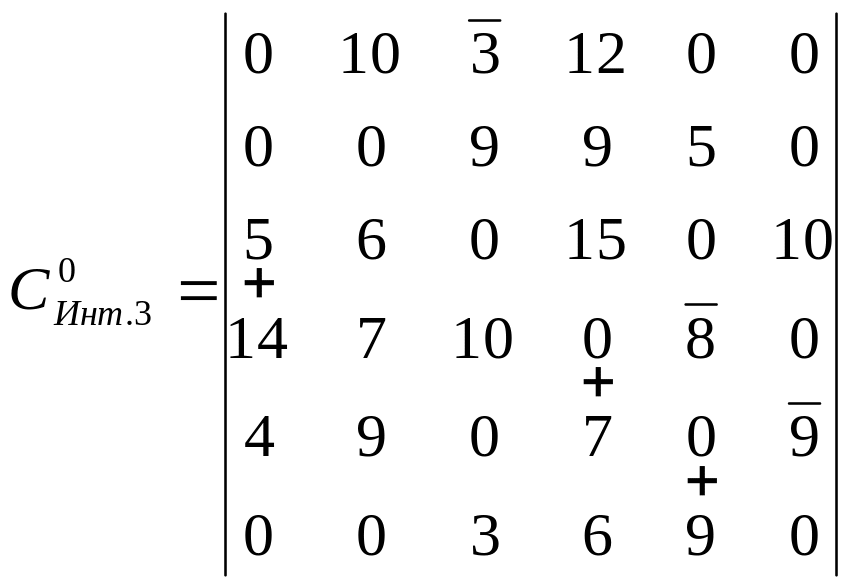
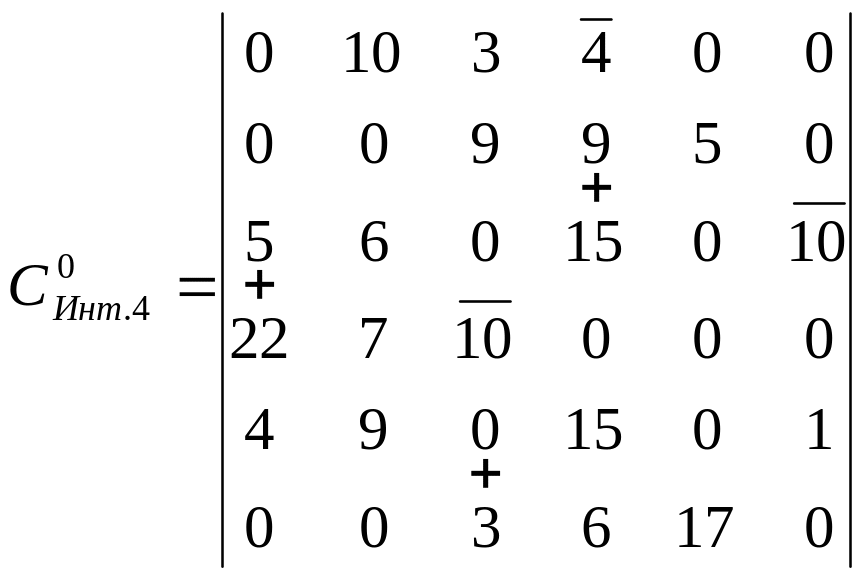
Ітерація 3 Ітерація 4

1456  = 8 1436  = 4

Ітерація 5 Ітерація 6

136  = 3 1256  = 1

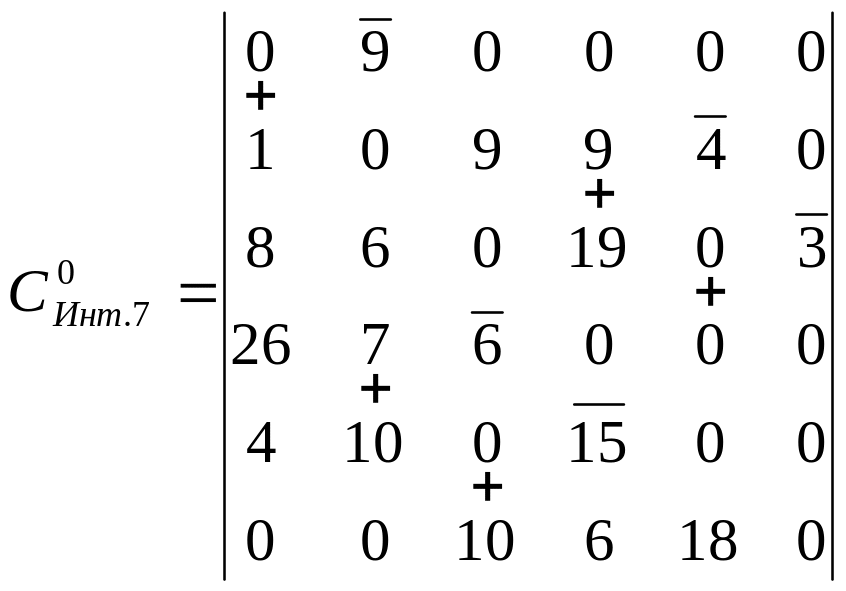
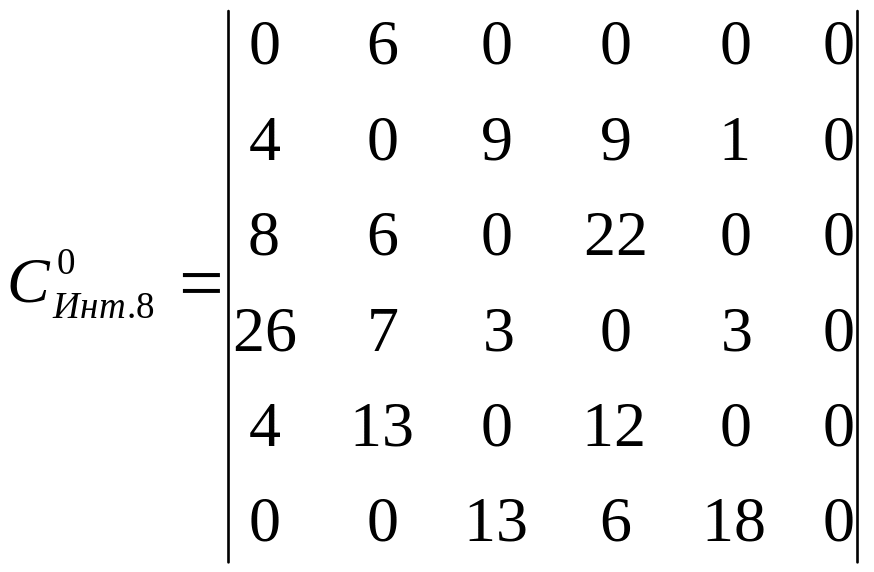
Ітерація 7 Ітерація 8

125436  = 3 ланцюг не побудований

2. Обчислення максимального потоку:

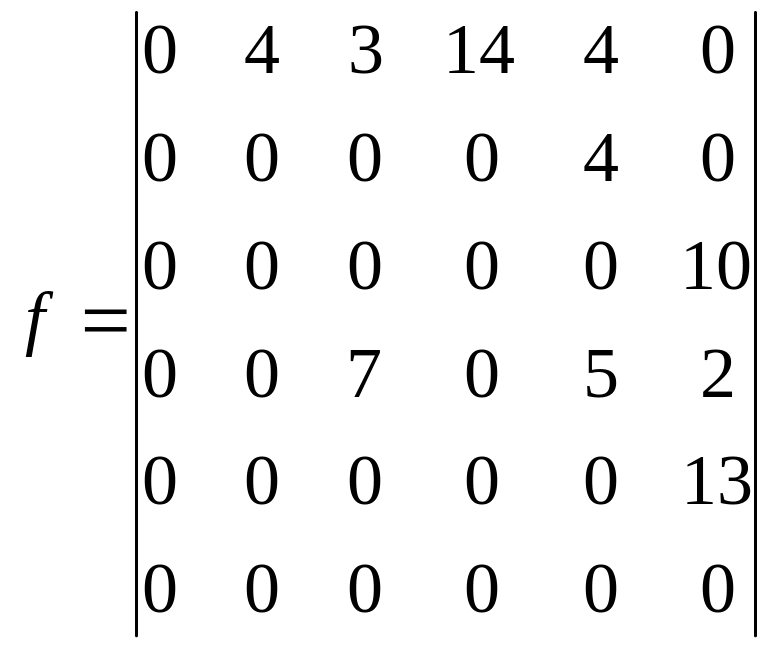
Шляхопровід (розв'язок) необхідно зробити на 4 вузлі.

Задача про мінімальний остов.

Задано перелік дисплейних класів. Потрібно провести кабель між аудиторіями без виникнення короткого замикання.

Остов = 0 L=min

i=1,N-1

Остов = 1

- вибір найближчого вузла до остова

- фіксуємо вузол + дуга

Це єдиний алгоритм, що дає відсутність зациклення.

1) Розглянемо вузол 1 - обводимо в кружечок. Вибираємо мінімальний вихід в іншу дугу – це вузол 2 і так далі.

Останній етап:

65

L = 1+1+2+1+2+3+1+2 = 13

Сервер ставимо на 4.