Методи аналізу мереж. Потокове програмування. Оптимізація на мережах.

Приклади:

1. Календарне планування. Критичний шлях.

2. Задача найкоротшого шляху.

3. Задача найкоротшого шляху для багатополюсних мереж. Алгоритм Флойда.

4. Задача про максимальний потік (небезпечні ділянки, завантажені вузли, скільки машин пропускається за визначений час).

5. Укладка кабелю мінімальної довжини (задача про мінімальний остов), організація обчислювальної мережі у ВУЗі.

6. Дано мережу, треба визначити де ставити насос. Визначити, де в місті ставити в'їзд, де виїзд для транзитного транспорту (Гоморі-Xy).

Мережею або графом називається множина вершин і дуг, взаємозалежних між собою. G=(V, D).

Дуга:

1 . Неорієнтована дуга - дуга, що має потік i, j, як у прямому, так і в оберненому напрямку.

0  fij  cij - обмеження.

cij - пропускна спроможність дуги або мережі.

cij  {0,1} - для задач найкоротшого шляху. Кожна дуга може характеризуватися cij, tij, dij - довжина або час переміщення по дузі.

2. Орієнтована дуга.

3 . Біорієнтована дуга.

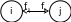
За допомогою біорієнтованої дуги можна описати орієнтовані і неорієнтовані дуги.

В залежності від дуг мережі класифікуються на орієнтовані, неорієнтовані та біорієнтовані.

Мережа називається зв’язаною, якщо можна з будь-якої точки потрапити в будь-яку іншу точку.

- це не зв’язана мережа.

Мережі можуть бути:

• однополюсні,

• багатополюсні.

В однополюсних мережах стік і початок задаються жорстко. Задача СПУ є однополюсною.

Для багатополюсних мереж стік і початок є перемінними, тобто S та T – змінні полюси.

Fij - потік для мережі або пропускна спроможність мережі, не обчислюється арифметично, а тільки шляхом моделювання. Моделювання є функцією для всіх потоків:

У кожній мережі можна виділити якусь частина G=(V^*,D^*).

Наприклад:

Ланцюг 1234

Fij = min {fij} _ij  G для всіх ділянок, що належать графу

Цикл - це ланцюг, де закінчення останньої дуги є початком першої. 12341.

Контур - це цикл, що має найбільшу довжину.

Д ерево - це частина мережі без циклу.

Для кожного вузла мережі діє закон Кірхгофа (сума вхідних потоків дорівнює сумі вихідних потоків).

Остов - дерево, що охоплює всі вершини мережі.

Розріз – це частина мережі, що робить мережу не зв’язною.

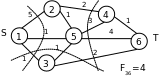
Пропускна спроможність розтину дорівнює сумі пропускних спроможностей дуг Fp = 7.

Теорема:

Пропускна спроможність мережі дорівнює мінімальному розрізу (або максимальному потокові).

F16 = 5 F24 = 5 F36 = 4

Класи задач мережної оптимізації.

1. Задача про найкоротшу відстань (найкоротший цикл, ланцюг).

2. Задача про мінімізацію мережі (пошук мінімального остова).

3. Задача про календарне планування (окремий випадок про найкоротшу відстань, задача керування проектом).

4. Визначення максимального потоку і пропускної спроможності мережі (аналіз надійності мережі).

5. Визначення полюсів із метою забезпечення максимального потоку.

6. Рішення комбінаторних задач, що можуть містити такі етапи:

• Генерація мережі або графа шляхом моделювання;

• Використання алгоритмів мережної оптимізації (вибирається оптимальна частина мережі).

Засоби представлення мереж.

Існує чотири засоби представлення мереж:

• за допомогою матриці суміжності;

• за допомогою матриці інцидентності;

• за допомогою вузлів (подій);

• за допомогою потоків, дуг (робіт) по кожному вузлі.

1. Матриця суміжності.

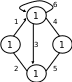
 1, якщо є дуга з вершини i у вершину j

Xij = 

 0, інакше

Xij  X

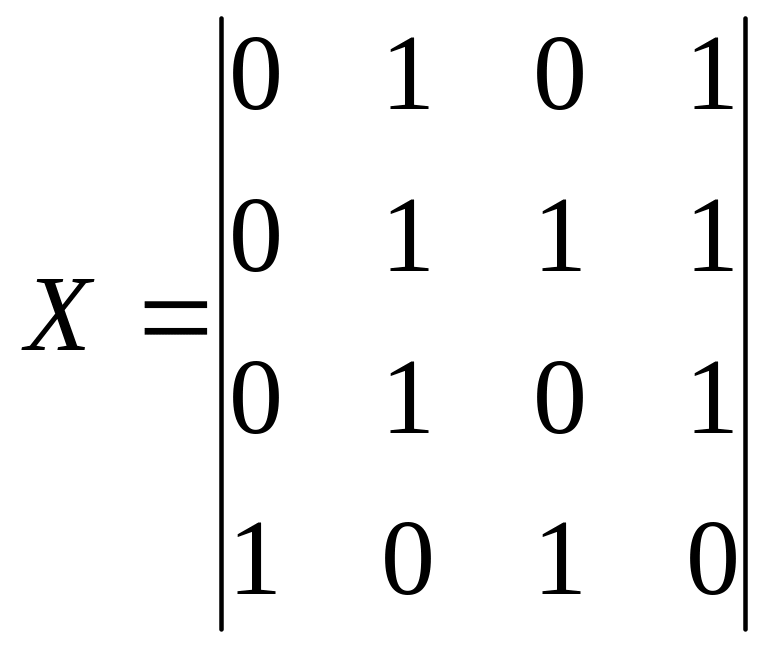
2. Матриця інцидентності.

 1 Якщо з вершини i випливає дуга j (ij) ;

Zij = -1 якщо у вершину i випливає дуга j (ij) ;

 0 інакше .

Zij  Z

3. Вузли.

- для орієнтованої мережі:

- для біорієнтованої мережі:

4. Потоки, дуги.

Цей засіб легше всього програмується, але займає багато пам'яті:

Засіб використовується тільки для орієнтованих мереж (задача СПУ).