Комбінаторний метод

2)Дискретне динамічне програмування (без сімплекс методу, на основі "лавинообразного" дослідження варіантів).

Потрібно сформувати рівні, кожен рівень при програмуванні створюється памяттю.

а)ОДЗ для кожного Х можна збудувати шляхом перевірки кожного обмеження

x₁= [0,0]

x₂= [0,2]

б) Динамічне дискретне программування на основі "лавинообразної" перевірки варіант.

3)Методи відкидання (методи Гоморі 1,2).

Суть методу в слідуючому:

а) отримання першого рішення методом Simple або Double методом

б) на основі максимальної дробової змінної формуються нові обмеження (відкидання дробової частини).

в) рішення нової системи рівнянь, розмірністю (m+1; n+1)

г)повторення пунктів б) і в) доки рішення не буде цілочисельне.

Гоморі –1 : для умови коли всі змінні повинні бути цілечисельним.

Гоморі –2 : частково (не на всі змінні накладається умова цілочисельності).

4) Метод (принцип) Розгалужень і обмежень.

5)Адитивний алгоритм (будується на постійному додаванніі) для задач Булевої оптимізації.

Задача про рюкзак (задача управління передачі файлів в режимі електронної пошти )де

Σс_ix_i->min ,

Σa_ix_i≤ b_j j=1,N

x_i є {0,1}

x_i – брати річ (файл) з собою;

с_i – цінність речі (розмір файлу);

a_i – маса речі (розмір файлу);

b_j – об’єм рюкзака (швидкість передачі даних, помножена на час передачі).

Метод відкидання Гоморі_1

Алгоритм можна зобразити слідуючою схемою.

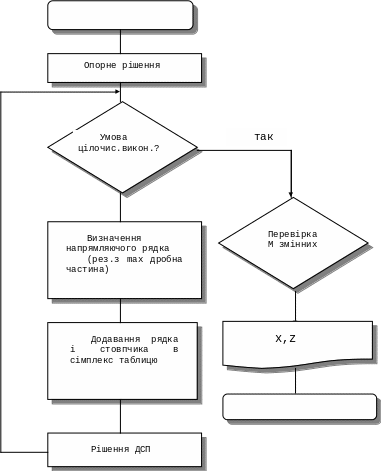
Використовуючи см-метод, ДСМ. Розв’язок може бути цілочисельним і нецілочисельним.

Якщо стовпчик А₀ – всі значення цілі -> рішення знайдено.

Якщо значення дробове – виділяємо стовпчик для відкидання дробової частини

Приклад Гоморі_1.

7х₁+9х₂->max

-х₁+3х₂+х₁ =6

7х₁+х₂+х4 =35

х_1,...х₄ є {0,1,2,...}

7 9 0 0

С_х В_х А₀ А₁ А₂ А₃ А₄

0 х₃ 6 -1 3 1 0

0 х₄ 35 7 1 0 1

∆ -7 -9 0 0

В даному випадку використовується Simple метод.

Неприпустимого рішення в нас немає (А₀) -> Simple метод. Базис х₂ х₁

А₀ А₁ А₂ А₃ А₄

х₂ 3.5 0 1 0.318 0,045

max число -> х₁ 4.5 1 0 -0,1 0,135

Умова нецілочисельності – вибираємо направляючий рядочок і додаємо обмеження (на основі 0.5).

Z =63;

Х =(4.5,3.5,0,0).

Формуємо нове відкидання і добавляємо нову змінну х₅

А₀ А₁ А₂ А₃ А₄ А₅

х₂ 3.5 0 1 0.318 0,045 0

х₁ 4.5 1 0 -0,1 0,135 0

х₅ –0.5 0 0 -0.9 -0.136 1

∆ 0.3 0 0 2.545 1.364 0

Х=(4.5; 3.5; 0; 0), 7 ітерацій

Х=(4,2; 1,4; 1; 1; 0)

Z=54

Цілочисельне програмування гоморі 2.

Використовується у випадку , якщо всі змінні чілочисельні.

Алгоритм Гоморі 2 аналогічний до Гоморі1

a_i0=b_i , якщо j=0

, якщо x_j-ціле та

y_i = , якщо x_j-ціле та

, якщо x_j-не ціле та a_ij0

, якщо x_j-не ціле та a_ij0

Метод "Розгалужень та обмежень".

Метод (принцип) Бренч & Браунд - Метод розгалужень та обмежень.

Принципи МРО.

1)Розгалуження. На основі вибраної стратегії та типу задачі розроблено алгоритм будування дерева (розгалуження).При цьому розгалуження в довжину і ширину

2)Рекорд – максимальне значення або максимально можлива оцінка, яку можна отримати в кінці розгалуження.

Не завжди рекорд можна вирахувати.

3) Оцінка – це поточний стан розгалуження, яке потрібно порівняти з Z≤ .

Якщо немає можливості такої операції, необхідно "тягнути" в пам’яті всі Z і визначити найкращі Z.

4)Відкидання - вибрати краще одне чи декілька розгалужень, найгірше відкинути і забути, погане відкласти в сторону для подальшого аналізу.