Рішення транспортної задачі

“МЕТОД ПОТЕНЦІАЛІВ”

Даний термін здобуто із теоретичних основ електротехніки.

Нехай була задана слідуюча умова:

А(11,11,8);

В(5,9,9,7).

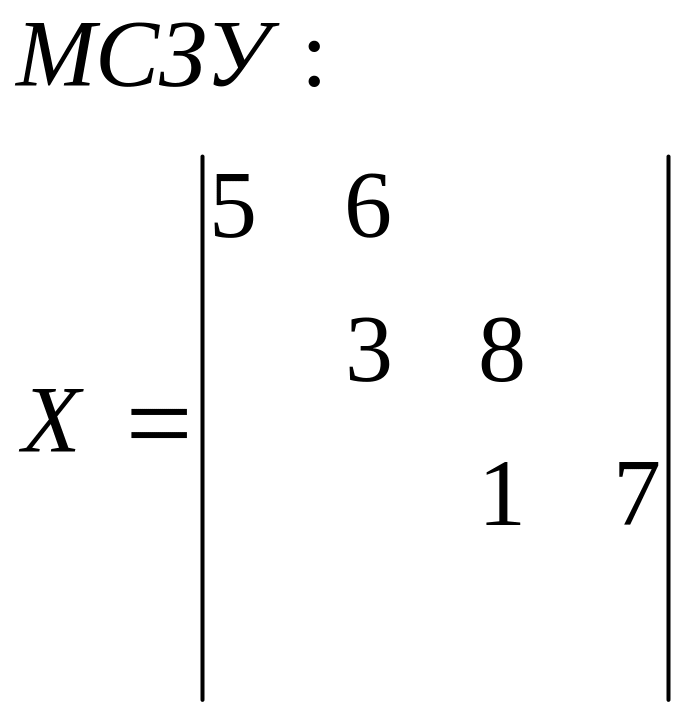
Побудова плану комунікацій та розрахунок потенціалів.

u

v

a₁

a₂

a₃

b₁

b₂

b₃

b₄

v₁=7

v₂=8

v₃=9

v₄=10

u₁=0

u₂=4

u₃=8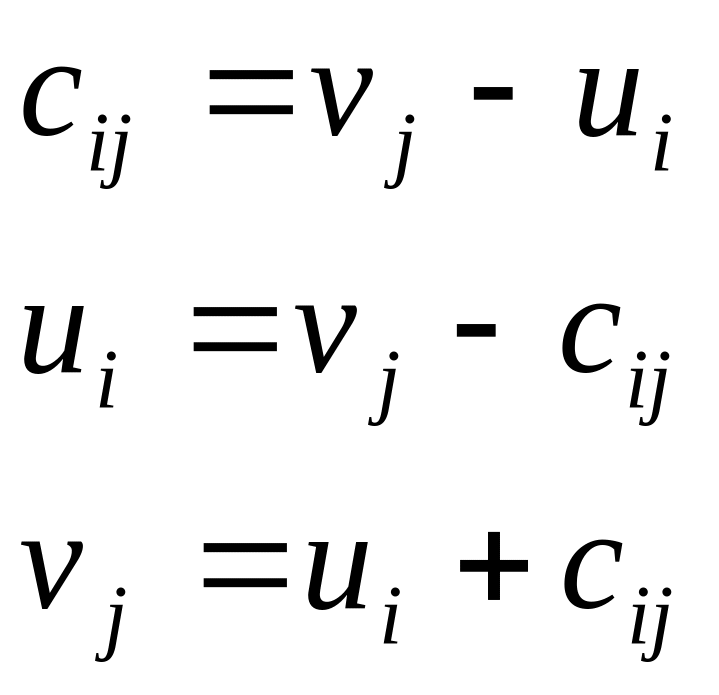

U=(0,4,8);

V=(7,8,9,10).

Будуємо оцінювальну матрицю С₀.

v

0

4

8

7 8 9 10

u

Циклічний процес:

1)Пошук направляючого елемента:

;

Якщо направляючий елемент не знайдено,то рішення отримано в матриці X.

2)Побудова в матриці X замкненого ланцюжка. (Направляючий елемент для даної задачі (-7)). Визначення -мінімальний елемент серед непарних.

=min(x₁,x₃,x₅,…);

=min(6,7,8)=6

3

Значення ЦФ корегується:

Z=Z-=150-7*6=108

)Перерахунок матриці X: віднімаємо в ланцюжку  з непарних та додаємо  до парних.

ПРИМІТКА:

1)ЦФ повинна поліпшуватися(окрім випадку,коли направляючий елемент  дорівнює ).

2)Контроль вірності обчислювань повинен завжди дорівнювати поточній митриці X на вичаткову матр.С:

3)Перерахунок матр.С₀:

а

+7

)послідовно викреслюємо рядок, починаючи з напрямляючого елемента; потім викреслюємо стовпець по істотним нулям, і т.д. до тих пір,поки всі істотні нулі не будуть викреслені.

-7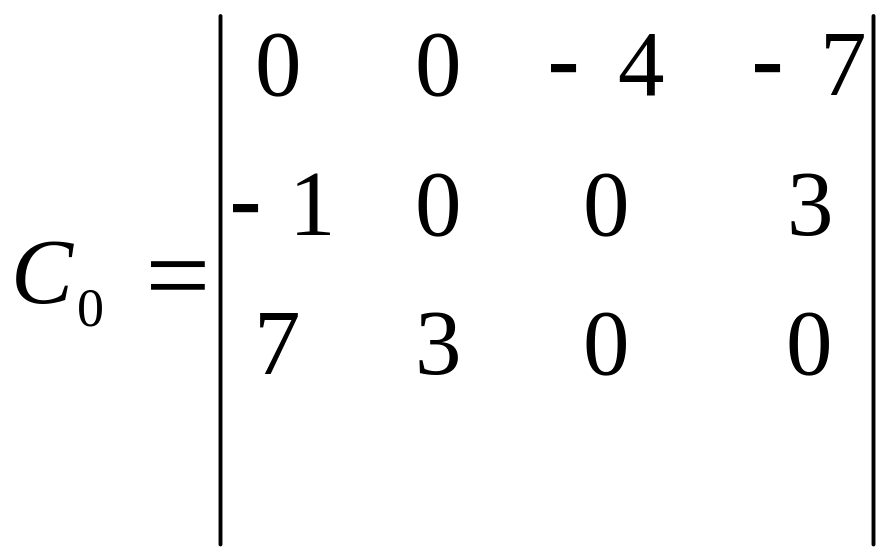

Істотний нуль: коли , а якщо  , X_ij.

б)Додавання до рядків “”;

віднімання від стовпців “”.

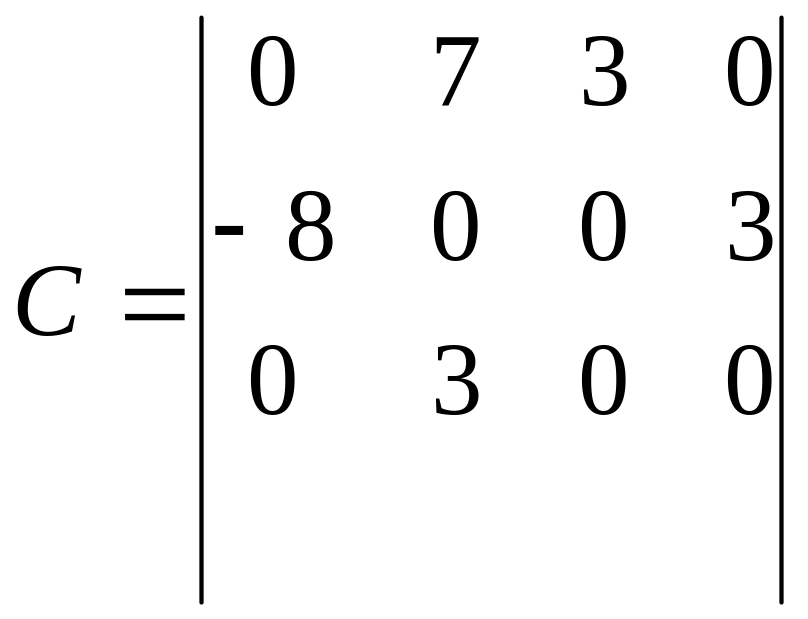
Ітерація 2.

Ланцюжок: (2-1)

(2-3)

(3-3) =min(2,1,5)=1

(3-4)

(1-4)

(1-1)

(2-1)

Z=108-8=100;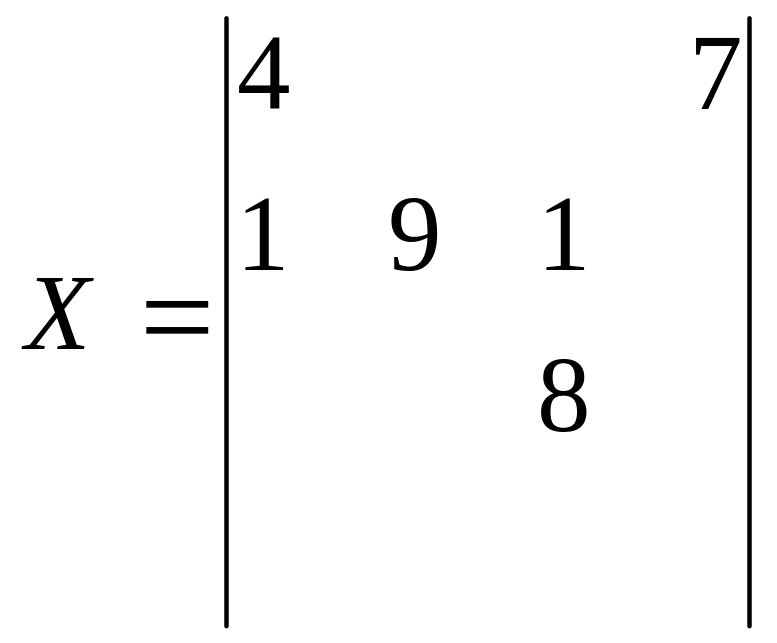

Ітер.3.

Ланцюжок: (1-3)

(1-1)

(2-1) =min(4,1)=1

(2-3)

(1-3)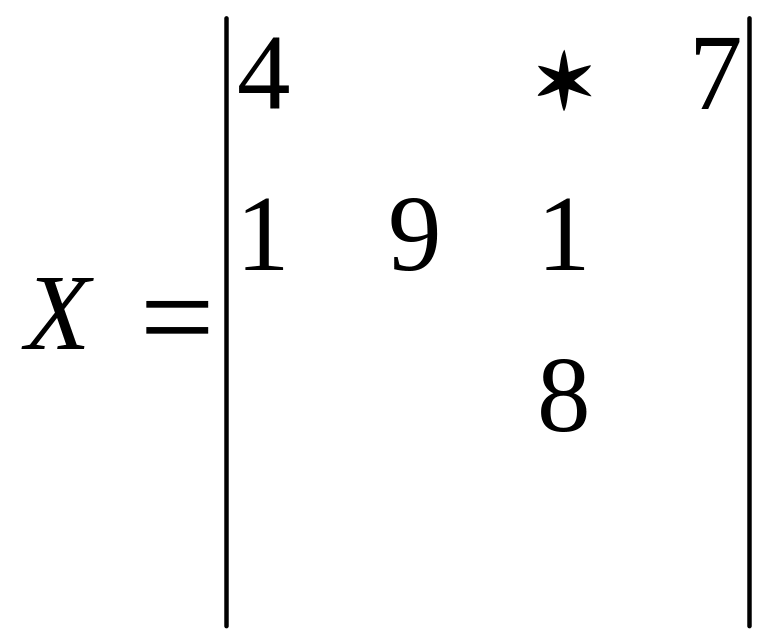

Z=100-5*1=95

І

Ланцюжок : (3-2)

(3-3)

(1-3)

(1-1)

(2-1)

(2-2)

(3-2)

тер.4

=min(8,3,9)=3

Z=95-3*2=89

Z=4*5+7*3+5*2+6*4+3*3+5*1=89

Рішення знайдено.

27