_{МЕТА :}

_{За допомогою деталей математичних операцій прийняти рішення .}

_{Дослідження операцій – це наука про моделі,методи оптимізації та систему прийняття рішень за допомогою оптимальних рівнянь. Знаючи “Дослідження операцій (ДО) ”,необхідно скласти модель, привести її до типової , обрати один чи декілька методів рішення та розв’язати задачу. Отримавши вектор-результат, потрібно повернутися до початкових змінних та проаналізувати їх на чутливість.}

_{Математична модель – це умовний об’єкт у формі більш зручній та доступній, ніж сам об’єкт, що розглядається.}

ОЗНАКИ МАТ. МОДЕЛІ:

_{- наявність цільової функції, що прямує до оптимуму (екстремуму) ;}

_{- наявність обмежень (=,>=,<=) ;}

_{- додаткові умови ( невід’ємність, цілісність ) ;}

_{- взаємозвязаність змінних в цільовій функції ,обмеженнях та додаткових умовах ;}

_{- належність моделі до певного середовища ( лінійне, нелінійне, динамічне програмування).}

_{X* , Z}

_{C – коефіцієнти цільової функції ;}

_{а – матриця а – коефіцієнти лівої частини обмежень ;}

_{b – коефіцієнти правої частини обмежень ;}

_{x – зміннаX* - відповідь ;}

_{Z – значення цільової функції,котре не можна поліпшити.}

ЗАДАЧА

Фірма має можливість рекламувати свою продукцію, використовуючи радіо та телебачення . Витрати на рекламу у фірми обмежені – 1500$ в рік . Кожна хвилина на радіо коштує 5$,на телебаченні - 100$ .Фірма хотіла б використовувати

телебачення не меньш ніж в 2 рази частіше, ніж радіо. Досвід минулих років показав , що обсяг збуту , котрий забезпечує кожна хвилина на телебаченні , в 25 разів більша ніж хвилина на радіо.

Визначити кошторис розподілення засобів на рекламу за рік. Визначити мінімальну суму витрат для того щоб перевести всю рекламу на телебачення. Кількість хвилин на радіо не повинна перевищувати 20 хвилин на рік.

Х 1 –радіо; Х2- телебачення;

_{4) x1 + 25x2 = 0 , 5 , 10 , . . . .}

_{x1 = 25 ; x2 = -1 .}

_{5 ) 5x1 + 100x2 = 1500 ; x = ( 20 ; 14 ) ;}

_{x1 = 20 ; z = 370 ;}

_{6) 5x1 + 100x2 = 1500 ; x = ( 7.3 ; 14.6 ) ;}

_{2x1 – x2 = 0 ; z = 150.}

_{Відповідь : z=370; x1 = 20 ; x2 = 14 .}

ЗАДАЧА

_{Розчинний вузол виробляє бетон 2}^х _{марок , вартість яких відповідно 2 тис. та 5 тис. за тону . Потужність вузла обмежена : 5 тон в зміну .Попит на 2}^у _{марку вище ніж на 1}^у _{не менше тони.}

_{Необхідно визначити роботу БРУ на протязі 3}^х _{змін,забезпечивши при цьму максимальний прибуток .}

Відповідь : x = ( 0 , 15 ) , z = 75 ; x = ( 7 , 8 ) , z = 54 .

ЗАДАЧА

Організувати випуск виробів залізобетонних конструкцій , на які необхідні ресурси .

Визначити план випуску виробів , виходячи з випуску ресурсів .

Z=54; X = (6, 5).

Основні етапи дослідження операцій

1. Постановка задачі ( тип моделі, тип задачі, можливість приведення її до типової, надмірність та достатність інформації );

2. Розробка математичної моделі (одиниця виміру, цільова функція, обмеження, ОДР);

3. Класифікація моделей;

4. Вибір та обгрунтування методів рішення;

5. Аналіз результатів та дослідження на чутливість.

Класифікація моделей та методів

1. Метод технічного розшуку моделей та рішень(Систематизація мислення).

2. Лінійне програмування .

3. Нелінійне програмування .

4. Динамічне програмування .

5. Дискретне програмування .

6. Потокове програмування чи оптимізація на мережах (сітях).

7. Багатокритеріальні задачі .

8. Стохастичне програмування або задачі масового обслуговування .

9. Евристичне програмування .

Типові класи задач

1. З адача про сортамент

V1 , . . . , Vn – вироби ;

C1 , . . . ,Cm – коефіцієнт прибутку , собівартості , реалізації тощо .

2. Задача про рекламу .

3. Задача змінно-добового планування .

4. Задача про ремонт та заміну обладнання .

5. ^{Задача про теорію розкладу. Проблема розкладу в ВНЗ. Одна з них : для кожної пари є аудиторії та потоки. Потрібно розвантажити сходи.}

і=1,M j=1,N

Xij0

6. Задача про вибір маршруту. Визначити найкоротшу відстань (шлях) від п. А до п. В маючи на увазі наявність пального.

Задачі сітьового планування та управління (СПУ) . Дана сіть , що описує деякий технологічний процес.

Лінійне програмування Лінійне програмування використовується лише тоді , коли Цільва фукція та одр – лінійні. Приклад

5x₁ - 6x₂ + x₃  min

2x₁ + 3x₂ - 4x₃ = 5

5x₁ + 6x₂  7

7x₁ + 3x₂  8

x_{1 ,} x₂  0

п риведемо рішення та обмеження до канонічного виду

f(x)  max

g_i(x) = b_i , i = 1,N

x  0

використовуємо графічний метод.

Варіанти використання графічного методу :

В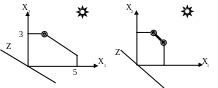 ідповідь: 1 рішення Відповідь : множина рішень на

прямій ( z  цій прямій )

Відповідь: 1 рішення Відповідь: немає рішень Відповідь: немає рішень

( ОДР необмежена знизу) (ОДР необмежена зверху) (ОДР порожня множина)

Примітка: ОДР для ЛП завжди випукла; вогнутостей не може бути.

СИМПЛЕКС МЕТОД або

Метод симплекс таблиць

Метод засновано на табличних перетвореннях (Джордана-Гауса) моделі, що представлена в канонічному вигляді . Канонічний вигляд моделі – це вигляд, необхідний для роботи з методом чи з програмою на ЕОМ . Для кожного методу існують свої вимоги до канонічного вигляду .

Вимоги для приведення до канонічного вигляду (для даного метода) :

Z(f)  max , Z(f) – цільова функція ;

Наявність обмежень типу “рівність” ;

Наявність одиничного додатнього базису ;

Додатність правої частини ;

Невід’ємність змінних ;

Наявність додатнього опорного рішення .

Базисна змінна – змінна, яку потрібно додати в обмеження для отримання рівності та одиничного вектора .

Штучна змінна (M –змінна)- змінна, яку необхідно дописати в обмеження в якості базисної , а якщо необхідно – і в цільову функцію з коефіціентом М, з метою отримання при рішенні нуль.

Приклади приведення до канонічного вигляду :

1) 3x₁ + 2x₂  min -3x₁ – 2x₂  max Розмірність задачі 2 * 4

6x₁ - x₂ 5 6x₁ - x₂ + x₃ = 5 -3 -2 0 0

7x₁ + x₂  7 7x₁ + x₂ + x₄ = 7 6 -1 1 0 5

x_{1 ,} x₂  0 x₁ , … , x₄  0 7 1 0 1 7

Відповідь : X = ( 0 , 0 , 5 , 7 ).

2) 3x₁ + 2x₂  min -3x₁ - 2x₂ – 30x₅  max 2 * 5

6x₁ - x₂  5 6x₁ - x₂ + x₃ =5 -3 -2 0 0 0

7x₁ + x₂  7 7x₁ + x₂ – x₄ + x₅ = 7 6 -1 1 0 0 5

x₁ , x₂  0 x₁ , … , x₄ 0 7 1 0 -1 1 7

Відповідь : X = ( 0 , 0 , 5 , 0 , 7 ) .

30x₄ 30 x₅

3) 3x₁ + 2x₂ max 3x₁+2x₂  max 3x₁+2x₂-Mx₄-Mx₅max 2 * 5

6x₁ - x₂  -5 -6x₁+ x₂5 -6x₁+ x₂-x₃+x₄=5

7x₁ + x₂ = 7 7x₁+ x₂ = 7 7x₁+ x₂+x₅=7

x₁ , x₂  0 x₁ , x₂  0 x₁ , … , x₅  0

Відповідь : X = ( 0 , 0 , 0 , 5 , 7 ) .

4) 7x₁ + 2x₂ min -7x₁–2x₂+2x₃-Mx₅max

6x₁ - x₂  5 6x₁- x₂+x₃+x₄=5

7x₁ + x₂ =-7 -7x₁- x₂+x₃+x₅=7

x₁ , x₂ 0 x_1,…,x₅  0

Введемо заміну x₂ = x₂ - x₃

АЛГОРИТМ ПРИВЕДЕННЯ ДО КАНОНІЧНОГО ВИГЛЯДУ

Аналіз умови невід’ємності . Якщо не для всіх змінних задана умова невід’ємності, то кожну таку змінну (невід’ємну) замінюють різницею двох додатніх .

Права частина повинна бути додатньою . Якщо в будь яких обмеженнях права частина від’ємна, необхідно помножити її на (-1) для корегування знаку .

Якщо цільова функція Z(f)  min ,то необхідно змінити коефіцієнти на протилежні , а Z(f)  max .

Для кожної нерівності типу “” додаємо базисну змінну .

Якщо обмеження типу “=” , додаємо одну М-змінну (велике вигадане число , напр.,10,20,...) .

Якщо обмеження типу “ ” ,додаємо різницю двох додатніх , одна з яких М-змінна.