7.2.3 Кривые течения нефтей и нефтепродуктов

Для обычных низкомолекулярных жидкостей (светлые нефте­продукты, легкие нефти) графики зависимостей между касательным напряжением сдвига τ в данной точке потока и скоростью сдвига S, определяемой по формуле (7.1) в той же точке, или так называемые кривые течения, представляет собой прямые 1, 2 или 3 (рис. 7.3), проходящие, через начало координат.

,

(7.1)

где du – скорость сдвига слоев жидкости друг относительно друга; dn – бесконечно малое расстояние между слоями жидкости.

Зависимость 1 (рис. 7.3) характерна для ньютоновской жидкости, поскольку ее тече­ние подчиняется закону трения Ньютона (7.2).

,

(7.2)

где  - динамическая (ньютоновская) вязкость жидкости.

Ньютоновская вязкость численно равна тангенсу угла наклона прямой 1 к оси S (рис. 7.3).

Рис. 7.3 Кривые течения жидко­стей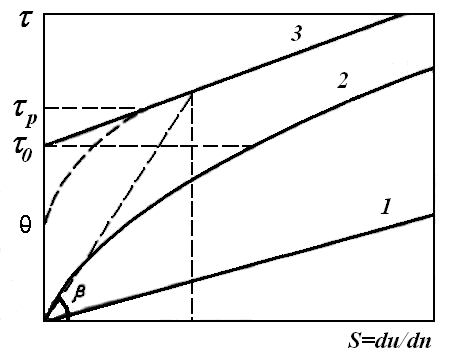

Течение растворов высокомолекулярных жидкостей и свободнодисперсных систем качественно совпадает с течением гомогенных жидкостей. При ламинарном режиме течения пропорциональность между напряжением сдвига и скоростью сдвига сохраняется, а прямая проходит через начало координат (рис. 7.3). Количественное же от­личие выражается в том, что вязкость системы оказывается выше вязкости чистой жидкости. Это вызывается тем, что крупные мо­лекулы и дисперсные частицы оказывают дополнительное сопротив­ление перемещению слоев жидкости. При этом может образоваться дисперсная система, характеризующаяся пластическими или вязкопластическими свойствами. Первая подчиняется закону трения Бингама (7.3) (модель жидкости – тело Бингама [25, 27]). Вторая – закону трения Шведова-Бингама (7.4) (модель жидкости – тело Шведова [152, 153]).

,

(7.3)

где  – структурная вязкость;  – статическое напряжение сдвига.

,

(7.4)

где ₀ – динамическое напряжение сдвига.

Структурированные жидкости уравнению Ньютона не подчи­няются, так как при их течении утрачивается свойство пропорцио­нальности между приложенной нагрузкой (напряжением сдвига) и вызываемой ею деформацией (скоростью сдвига). Жидкость про­должает сохранять способность к течению при сколь угодно малых напряжениях сдвига. По мере увеличения скорости сдвига в жид­кости происходит разрушение еще слабых связей между агрега­тами, упорядочение взаимного положения и ориентация частиц относительно направления потока. Все это приводит к относитель­ному уменьшению прилагаемого к жидкости напряжения сдвига, и кривая течения 2 (см. рис. 7.3) становится обращенной вы­пуклостью к оси τ.

Системы, в которых жидкая фаза иммобилизована сплошной структурной сеткой, приобретают способность к течению только после разрушения сетки. В соответствии с моделью Шведова - Бингама (7.4) течение таких жидкостей начинается после приложения к ним напряжения сдвига большего, чем предельное напряжение сдвига τ₀, причем с началом течения структура полностью разру­шается и жидкость течет затем как ньютоновская. Идеальное вязко-пластичное течение описывается прямой 3 (см. рис. 7.3), исходящей из точки τ₀ под углом к оси скорости сдвига, тангенс которого чис­ленно равен пластической (структурной) вязкости .

При рассмотрении кривых течения реальных вязкопла­стичных жидкостей можно наблюдать три характерные точки:  – напряжение сдвига, при котором начинается течение (статическое напряжение сдвига); τ₀ — динамическое (предельное) напряжение сдвига; τ_р— напряжение сдвига, при котором разрушение струк­туры заканчивается.

Многочисленные исследования реологических моделей нефтей показывают, что при температурах, близких к температуре засты­вания, нефти хорошо подчиняются модели Шведова-Бингама.

Переход от ньютоновских жидкостей к неньютоновским осуществляется плавно по мере понижения температуры.

Разрушение коагуляционных структур, в отличие от разруше­ния хрупких кристаллизационных, имеет свои особенности. После приложения определенной нагрузки к жидкости, обладающей структурой коагуляционного происхождения, немедленного раз­рушения структуры не наблюдается; степень разрушения зависит не только от скорости сдвига, при которой происходит разруше­ние, но и от времени воздействия нагрузки. Характерно, что после снятия нагрузки прочность структуры через определенное время восстанавливается полностью, а при уменьшении нагрузки – ча­стично, до той степени разрушения, которая соответствует остав­шейся уменьшенной нагрузке. Такая способность к самопроизволь­ному восстановлению структуры после ее разрушения называется тиксотропией.