5. Построение матрицы проверок

Пусть G(V,U) - упорядоченный граф с n вершинами, множество входов которого обозначим X={x₁,…,x_q} (q<n), а множество выходов - Y={y₁,…,y_p} (p>1).

Вершины x и z в графе G(V,U) образуют контрольную пару (x,z), если сигнал, подаваемый на вход элемента x, может быть снят на выходе элемента z, при этом вершина z графа G(V,U) называется контрольной точкой. Для того чтобы пара (x,z) была контрольной необходима достижимость вершины z графа G(V,U) из вершины x. Вектором проверки контрольной пары (x,z) называется n-мерный вектор b(x,z)=(b₁, b₂,…, b_n), компонента b_K которого равна 1, если существует хотя бы один путь от x к z, содержащий вершину к, и нулю – в противном случае.

Пусть для упорядоченного графа G(V,U) с n вершинам задано некоторое исходное множество Z={z} КТ и построены все возможные контрольные пары (x,z), где . Матрицей проверок B_z=llb_ijll (i= , j= ) на множестве Z контрольных точек называется матрица, в которой b_ij=1,если вершина j входит в проверку i-й контрольной пары, и b_ij=0 – в противном случае.

Пример 7. На рис. 2 приведены граф и матрица проверок объекта (КТ - вершины 6,7).

1 2 3 4 5 6 7

b(1,6)

b (2,6)

b(2,7)

Рис.2. Матрица проверок и граф объекта диагностирования.

5. Задания для самостоятельной работы

Задана матрица проверок B_i (i –номер варианта) и вероятности отказов блоков (варианты заданий в таблице 4).

Задание1. Определить коэффициент глубины диагностирования К.

Задание 2. Упорядочить точки контроля по количеству доставляемой информации.

Задание 3. Используя программу p1.exe (программу можно написать самостоятельно), получить диаграмму зависимости коэффициента глубины диагностирования от выбранного множества КТ и определить вероятность правильного определения состояния системы по результатам измерений (при использовании программы отменить опцию «Использовать улучшенный генератор»).

Таблица 4.

№ вар.	0	1	2	3	4	5	6	7	8	9
q1	0,1	0,01	0,02	0,1	0,04	0,05	0,1	0,07	0,08	0,1
q2	0,01	0,1	0,05	0,01	0,1	0,01	0,05	0,1	0,1	0,01
q3	0,05	0,1	0,1	0,05	0,05	0,1	0,01	0,01	0,1	0,05
q4	0,07	0,05	0,1	0,1	0,1	0,1	0,1	0,1	0,05	0,1

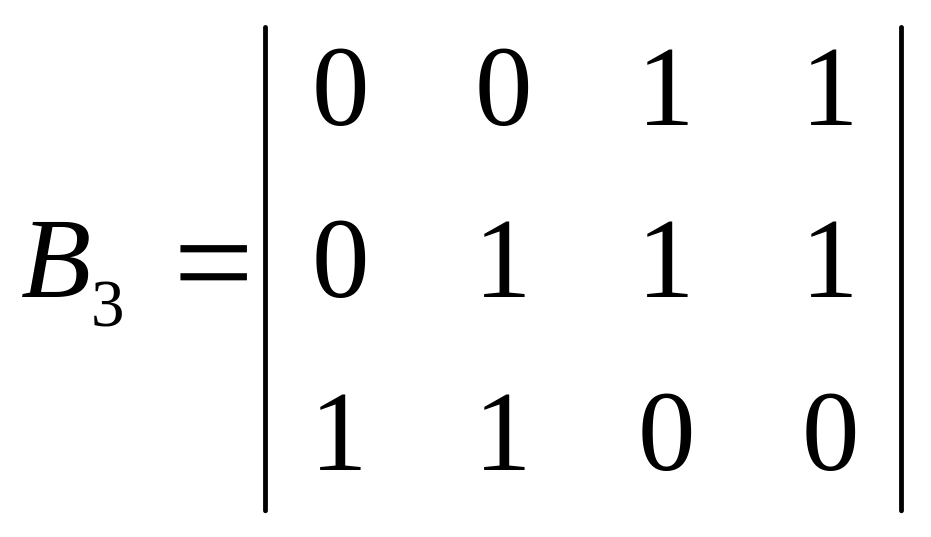
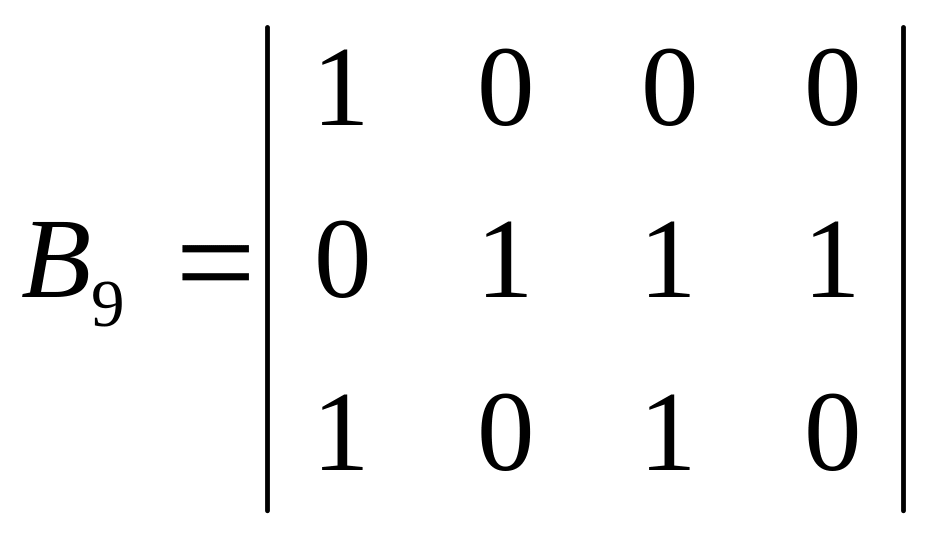
Задание 4. Для объектов диагностирования заданных в виде графов (рис. 3, 4,5) построить матрицы проверок, получить диаграммы зависимости коэффициента глубины диагностирования от множества КТ и определить вероятности правильного восстановления состояния системы по результатам измерений на выбранном множестве КТ (вероятности отказов всех блоков принять равными 0,01; КТ выбрать самостоятельно из заданных множеств).

КТ – вершины 20 – 25

Рис.3. Граф объекта диагностирования.

КТ – вершины 12 – 20.

Рис.4 Граф объекта диагностирования (вариант 3).