4. Восстанавливаемая информационная система

Рассмотрим функционирование информационной системы как многоканальную систему массового обслуживания с отказами, в которой поток требований на обслуживание - заявки на получение информации, заявка получает отказ в обслуживании, если все каналы заняты.

Вероятностью безотказной работы информационной системы является вероятность того, что ни одной из заявок не будет отказано в обслуживании за время t. Функцией готовности информационной системы называется вероятность того, что в произвольный момент времени t система готова принять заявку на обслуживание.

Предположим, что время между заявками и время обслуживания подчиняются экспоненциальному распределению с параметрами соответственно . Назовем i-м состоянием системы такое, в котором i каналов заняты обслуживанием, вероятности состояний p_i(t), i=0,1,…,n. Если система находится в n-м состоянии, очередная заявка получит отказ в обслуживании. В системах, работающих до первого отказа, отсутствует переход из отказового n-го состояния в (n-1)-е. Для систем многократного использования такой переход возможен, т.е. такая модель аналогична модели восстанавливаемой технической системы. Граф состояний системы приведен на рис.3.

Математическая модель функционирования системы многократного использования с отказами представляется следующей системой дифференциальных уравнений:

(22)

Функция готовности

. (23)

При стремятся к постоянным величинам и система (22) превращается в следующую систему линейных алгебраических уравнений

(24)

при условии

. (25)

Из (24,25) определяются предельные вероятности состояний

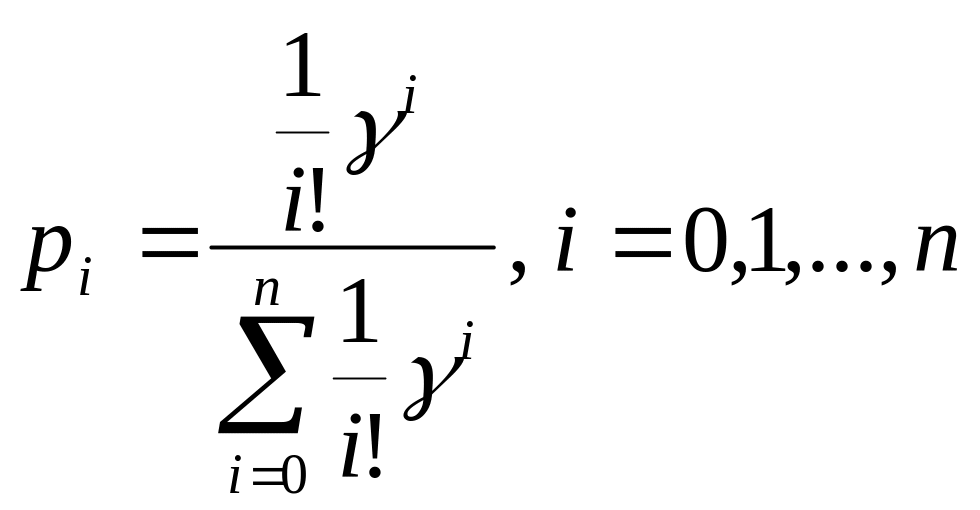. (26)

и коэффициент готовности

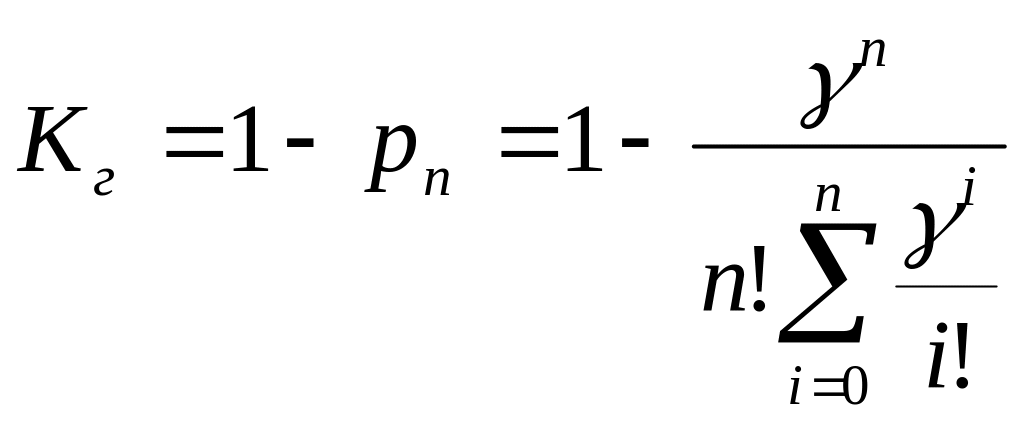. (27)

2. Последовательность выполнения работы

Получить у преподавателя номер варианта. При выполнении работы рекомендуется применение программных средств (Mathcad, Excel). Исходные данные для расчетов приведены в приложении.

1. Определение показателей надежности и риска восстанавливаемой нерезервированной системы (табл.1):

• определить наработку на отказ и среднее время восстановления;

• определить коэффициент готовности;

• построить графики функции готовности при интенсивностях восстановления и определить длительность переходных процессов;

• построить график функции риска и определить риск за время равное планируемому времени непрерывной работы t_пл.

2. Исследование надежности и риска восстанавливаемой системы с дублированием (табл.2, 0.01, 0.1, 1, 10,100).

2.1. Система, работающая до 1-го отказа:

• определить среднее время безотказной работы при нагруженном и ненагруженном режимах работы резерва;

• определить выигрыш в среднем времени безотказной работы за счет восстановления при нагруженном и ненагруженном дублировании и построить график функции .

2.2. Система многократного использования:

• определить коэффициенты готовности при двух режимах работы резерва, с одним и двумя каналами восстановления;

• произвести сравнительный анализ значений коэффициентов готовности при нагруженном и ненагруженном дублировании;

• произвести сравнительный анализ значений коэффициентов готовности при наличии одного и двух каналах восстановления;

• определить среднее время безотказной работы для двух режимов работы резерва;

• определить техногенный риск системы в течение планируемого времени непрерывной работы t_пл и в течение всего срока службы T_с при различных характеристиках обслуживания.

3. Исследование надежности информационной восстанавливаемой системы (табл.3).

• определить коэффициент готовности системы для 0.01, 0.1, 1, 10,100 при наличии n каналов обслуживания;

• определить число каналов обслуживания, которое при заданных обеспечивает заданное значение коэффициента готовности.

Отчет по лабораторной работе должен содержать

• цель работы;

• модели и алгоритмы решения задач;

• результаты в виде формул, графиков, таблиц;

• анализ полученных результатов и выводы.