Методические указания к лабораторной работе №2

по дисциплинам «Надежность ЭВМ и ВС»,

«Теория надежности технических систем»

Исследование надежности восстанавливаемых систем

ВВЕДЕНИЕ

Целью лабораторной работы является исследование свойств нерезервированных и резервированных восстанавливаемых технических и информационных систем, определение показателей надежности и риска при различных характеристиках обслуживания.

Практическое освоение методов анализа надежности позволит подтвердить теоретические положения, изученные в лекционном курсе, выявить влияние восстановления (ремонта) на надежность и риск технической системы, сделать важные выводы об эффективности применения мер по обеспечению и повышению надежности.

1. Теоретические сведения

1. Основные показатели надежности

P(t) – вероятность безотказной работы – вероятность того, что наработка до первого отказа превышает заданную величину t;

– интенсивность отказов;

– интенсивность восстановления;

T₀ – среднее время безотказной работы – математическое ожидание наработки до первого отказа;

T – среднее время работы между отказами (средняя наработка на отказ);

T_в – среднее время восстановления;

– параметр потока отказов – скорость изменения среднего числа отказов в момент t;

G(t) – функция готовности – вероятность того, что система исправна в момент t;

K_г – коэффициент готовности – вероятность того, что система будет исправной при длительной эксплуатации (стационарный режим);

K_п – коэффициент простоя – вероятность того, что система будет неисправной при длительной эксплуатации.

(1)

2. Восстанавливаемая техническая система без резервирования

Техническая система называется восстанавливаемой (ремонтируемой) если после устранения отказа она может продолжать выполнение своих функций. Восстановление системы представляет собой проведение необходимых работ по ремонту или замене отказавших элементов.

Будем рассматривать восстанавливаемые системы при следующих допущениях:

• время между отказами имеет экспоненциальное распределение с параметром ;

• время восстановления - экспоненциальное распределение с параметром ;

• в процессе восстановления новые отказы не появляются.

В этом случае среднее время безотказной работы невосстанавливаемой системы определяется как , поток отказов – пуассоновский с постоянной интенсивностью .

Система без резервирования может

находиться в двух состояниях:

0 - работоспособное,

1 - восстановление.

Граф состояний приведен на рис. 1.

Обозначим через p_i(t) вероятность пребывания системы в состоянии i.

Функционирование системы может быть описано следующей системой дифференциальных уравнений:

(2)

Решением системы при начальных условиях являются функции

(3)

Функция , представляющая собой вероятность того, что система работоспособна в момент времени t, является функцией готовности системы.

Предельные вероятности состояний при являются соответственно коэффициентами готовности и простоя системы:

(4)

Эти вероятности можно получить, не решая системы дифференциальных уравнений, если в (2) при положить и учесть . Средняя наработка на отказ и среднее время восстановления равны соответственно

. (5)

Если система состоит из n элементов, а интенсивности отказов и восстановления i элемента соответственно , то

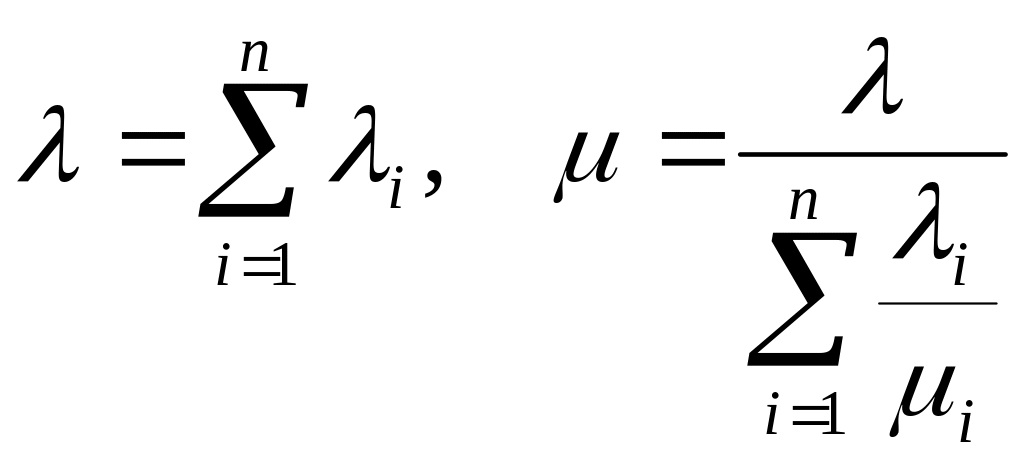. (6)

Техногенный риск системы представляет собой возможные потери из-за отказов элементов, выраженные в денежных единицах. Если задан риск из-за отказа i элемента , то функция риска и ее двусторонние оценки

(7)